
- •1. Первообразная и ее свойства
- •3. Таблица интегралов.
- •2.Неопределенный интеграл и его свойства
- •4.Замена переменной в неопределенном интеграле
- •5. Интегрирование по частям в не опред. Интеграле
- •6. Интегрирование выраж содержащ квадратный трехчлен
- •7.Интегрирование простых правильных дробей
- •9.Интегрирование некоторых классов иррац функций
- •10.Интегрирование тригонометрических выражений
- •11. Определение определенного интеграла и его св-ва
- •12. Интеграл с переменным верхним пределом;производная по верхнему пределу
- •13.Формула Ньютона-Лейбница
- •14.Замена переменной в определенном интеграле
- •15.Интегрирование по частям в определенном интеграле
- •16.Геометрические приложения определенного интеграла
- •17.Несобственные интегралы по бесконечному промежутку интегрир от непрерывных функций.
- •18.Несобственные интегралы по конечному промежутку интегрирования от неограниченных функций.
- •19. Диффер уравн: опред, решение уравн, задача Коши, общ и частн решения, геом смысл решений
- •20.Диффер уравнен первого порядка с разделенными и разделяющ переменными
- •21.Лин диффер уравнения 1го порядка(методы Бернулли и Лагранжа, их решения)
- •22.Лин диффер уравн 2го порядка с пост коэфф, структура их общ решения
- •23. Структура решения лин неоднор дифф уравн 2го порядка
- •24.Нахождение частных реш лин неоднор диффер уравн 2го порядка с пост коэфф по виду правой части
- •25. Числовой ряд и его сумма; сход и расход ряды
- •26. Геометрический и гармонический ряды
- •27. Необходимые условия сходимости ряда
- •28.Полож ряды; признаки сравнен их сходимости
- •29.Предельный признак Даламбера
- •30.Предельный признак Коши
- •31.Интегральный признак Маклорена-Коши
- •32.Знакоперемен ряды, абсол и условная сходимости
- •33.Теорема Коши об абсол сход знакоперем ряда
- •34.Признак Лейбница знакочеред рядов
- •35.Теорема Абеля сходимости степенного ряда
- •36.Радиус сходим степенного ряда и его нахождение
- •37. Понятие о рядах Тейлора и Маклорена
- •39.Разложение в ряд Маклорена ф-ции cos X, sin X
29.Предельный признак Даламбера
Пусть
в случае строго положительного ряда
существует предел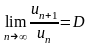 .
(29) Тогда при
.
(29) Тогда при
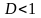 ряд сходится; при
ряд сходится; при
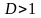 ряд расходится;
ряд расходится;
при
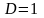 ряд может как сходиться , так и расходиться
(признак ответа не даёт).
ряд может как сходиться , так и расходиться
(признак ответа не даёт).
Доказательство. Условие (29) по определению предела последовательности означает следующее: для любого найдётся такой номер N, что для всех будут выполнены неравенства
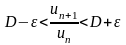 .
Действительно, в этом случае в силу
произвольности числа
его можно выбрать таким, чтобы выполнялось
неравенство
.
Действительно, в этом случае в силу
произвольности числа
его можно выбрать таким, чтобы выполнялось
неравенство
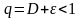 ( за положительное число
можно взять любое число, меньшее чем
( за положительное число
можно взять любое число, меньшее чем
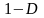 ).
Следовательно, по теореме 5 ряд сходится.
).
Следовательно, по теореме 5 ряд сходится.
Если
,
то, взяв
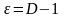 ,
получим, что
,
получим, что
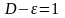 .
Тогда для
будет выполнено неравенство
.
Тогда для
будет выполнено неравенство
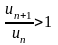 ряд расходится.
ряд расходится.
Покажем,
что при
ряд может как сходиться, так и расходиться.
Приведём по этому случаю примеры. Так,
для гармонического ряда
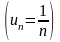 имеем, что
имеем, что
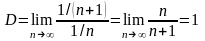 .Рассмотрим
теперь ряд с общим членом
.Рассмотрим
теперь ряд с общим членом
 .
И в этом случае
:
.
И в этом случае
:
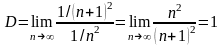 .Но
гармонический ряд расходится, а ряд
.Но
гармонический ряд расходится, а ряд
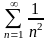 сходится.
сходится.
Признак
Даламбера целесообразно применять,
когда общий член ряда содержит выражения
видов
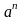 ,
,
 .
.
30.Предельный признак Коши
Пусть для положительного ряда (22) существует предел
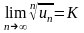 .
(32)Тогда при
.
(32)Тогда при
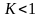 ряд сходится;
ряд сходится;
при
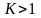 ряд расходится; при
ряд расходится; при
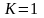 возможны как сходимость, так и расходимость
ряда.
возможны как сходимость, так и расходимость
ряда.
Доказательство. На основании определения предела последовательности условие (32) означает следующее: для любого найдётся такой номер N, что для всех будут выполнены неравенства
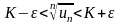 .
надо установить, что
.
надо установить, что
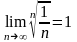 и
и
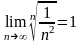 .Вычислим
только первый из этих пределов, так как
второй получится из первого на основании
равенства
.Вычислим
только первый из этих пределов, так как
второй получится из первого на основании
равенства
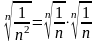 .
Для вычисления первого предела
(неопределённость вида
.
Для вычисления первого предела
(неопределённость вида
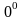 )
рассмотрим выражение
)
рассмотрим выражение
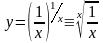 с непрерывной переменной
с непрерывной переменной
 .
Прологарифмируем это выражение и
докажем, что
.
Прологарифмируем это выражение и
докажем, что
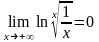 .
Действительно,
.
Действительно,
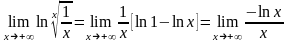 .
Для вычисления последнего предела
(неопределённость
.
Для вычисления последнего предела
(неопределённость
 )
применим правило Лопиталя:
)
применим правило Лопиталя:
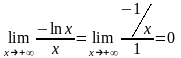 .
.
Так
как
,
то
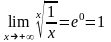 .
Теорема доказана.
.
Теорема доказана.
31.Интегральный признак Маклорена-Коши
Пусть
заданная на промежутке
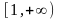 функция f(x)
непрерывна, неотрицательна и не
возрастает. Пусть положительный числовой
ряд имеет форму
функция f(x)
непрерывна, неотрицательна и не
возрастает. Пусть положительный числовой
ряд имеет форму
 ,
(34)т.е. члены ряда удовлетворяют условию
,
(34)т.е. члены ряда удовлетворяют условию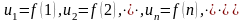 .
.
Тогда для сходимости ряда (1.34) необходимо и достаточно, чтобы сходился несобственный интеграл
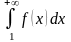 .
(35)Доказательство.
В силу монотонности функции
.
(35)Доказательство.
В силу монотонности функции
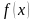 на любом отрезке
на любом отрезке
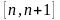
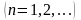 справедливы неравенства
справедливы неравенства
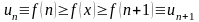 .
.
Так
как
,
 – постоянные числа и
– постоянные числа и
 ,
то, интегрируя эти неравенства по
отрезку
,
из свойств неопределённого интеграла
получим
,
то, интегрируя эти неравенства по
отрезку
,
из свойств неопределённого интеграла
получим
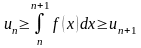 .
(36)Неравенства (36) позволяют обратиться
к признаку сравнения (теорема 3) для
следующих рядов:
.
(36)Неравенства (36) позволяют обратиться
к признаку сравнения (теорема 3) для
следующих рядов:
(37)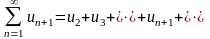 ,
(38)
,
(38)
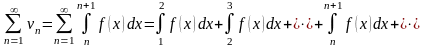 .
(39)
.
(39)
Рассмотрим ряд (39). Его n-й частичной суммой будет
 .Так
как
.Так
как
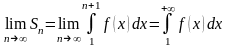 ,
сходимость ряда (39) означает сходимость
несобственного интеграла (35).
,
сходимость ряда (39) означает сходимость
несобственного интеграла (35).
Если
ряд (37) сходится, то по признаку сравнения
рядов в силу первого неравенства из
(36)
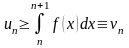 будет сходиться ряд (39) и, следовательно,
несобственный интеграл (35). Первая часть
теоремы доказана, т.е. установлено
необходимое условие сходимости.
будет сходиться ряд (39) и, следовательно,
несобственный интеграл (35). Первая часть
теоремы доказана, т.е. установлено
необходимое условие сходимости.
Пусть
сходится несобственный интеграл (35). В
силу ранее отмеченного будет сходиться
и ряд (39), общий член которого имеет вид
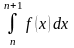 .
Тогда на основании признака сравнения
рядов в силу второго из (36) неравенства
.
Тогда на основании признака сравнения
рядов в силу второго из (36) неравенства
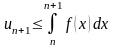 будет сходиться ряд с меньшими членами,
т.е. ряд (38). Поскольку ряд (37) отличается
от ряда (38) только первым членом
будет сходиться ряд с меньшими членами,
т.е. ряд (38). Поскольку ряд (37) отличается
от ряда (38) только первым членом
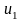 ,
то на основании замечания 4 будет
сходиться и ряд (37), т.е. исходный ряд
(34). Достаточное условие установлено.
Теорема доказана.
,
то на основании замечания 4 будет
сходиться и ряд (37), т.е. исходный ряд
(34). Достаточное условие установлено.
Теорема доказана.
Теорема 8 означает, что ряд (34) и несобственный интеграл (35) одновременно сходятся или расходятся.
