
- •19Достаточное услоие. Первый признак.
- •21.Точка перегиба. Достаточное и необходимое условия
- •Достаточное условие точки перегиба
- •26.2. Формула Тейлора для произвольной функции
- •23.Первообразная и неопределенный интеграл, их свойства
- •25Дробно-рациональная функция типы простейших алгебраических дробей и их интегрирование
- •26 27.Определенный интеграл римана, интегральная сумма, геом интерпритация, свойства
21.Точка перегиба. Достаточное и необходимое условия
Определение точки перегиба
Точка, в которой функция определена и в которой функция меняет направление выпуклости, называется точкой перегиба. В окрестности такой точки x 0 график функции y = f (x) слева и справа от точки x0 имеет разные направления выпуклости. Очевидно, что в точке перегиба касательная пересекает график функции так, что с одной стороны от этой точки график лежит под касательной, а с другой - над нею. В окрестности точки перегиба график функции геометрически переходит с одной сторон касательной на другую и "перегибается" через нее. Отсюда и произошло название "точка перегиба".
Необходимое условие точки перегиба
Теорема. Пусть функция y = f (x) дважды непрерывно дифференцируема на интервале (a, b). Для того, чтобы точка М(x0, f(x0)) была точкой перегиба графика функции y = f (x) необходимо, чтобы f " (x0) = 0. Доказательство. Предположим обратное, пусть f "(x0) ≠ 0. Тогда в силу непрерывности второй производной по теореме об устойчивости знака непрерывной функции существует окрестность точки x0, в которой f ″(x) < 0 (f "(x) > 0), и, значит график функции y = f (x) имеет определенное направление выпуклости в этой окрестности. Но это противоречит наличию перегиба в точке M(x0; f (x0 )). Полученное противоречие доказывает теорему. Не всякая точка М (x0, f (x0)), для которой f " (x0) = 0, является точкой перегиба. Например, график функции y = f(x) = x4 не имеет перегиба в точке (0; 0), хотя f " (х) = 12·x ² = 0 при х = 0. Поэтому равенство нулю второй производной является лишь необходимым условием перегиба. Точки М (x0; f (x0)) графика, для которых f "(x0) = 0, будем называть критическими. Необходимо дополнительно исследовать вопрос о наличии перегиба в каждой критической точке, для чего следует сформулировать достаточное условие перегиба.
Достаточное условие точки перегиба
Теорема. Пусть функция y = f (x) имеет вторую производную f "(x) в некоторой достаточно малой окрестности точки x0 интервала (a, b), за исключением, быть может самой точки х0, а график функции имеет касательную в точке С = (х0, f (x0)). Если при переходе через точку х0 вторая производная f "(x) меняет знак, то точка С является точкой перегиба графика функции y = f (x). Доказательство. Из того, что f "(x) слева и справа от точки x0 имеет разные знаки, то направление выпуклости графика функции слева и справа от точки x0 является различным. Это и означает наличие перегиба в точке M(x0; f (x0)).
22.понятие о многочлене Тейлора. Формула Тейлора для функций одной переменной (без док) , формула Маклорена
В определении функции у=ƒ(х) не говорится о том, при помощи каких средств находятся значения у по значениям х. В тех случаях, когда функция является формулой вида у=х3/5-5х+7, значения функции найти легко с помощью четырех арифметических действий. Но как найти значения, например, функций у=sinx, у=ln(1+х) при любых (допустимых) значениях аргумента?
Для того, чтобы вычислить значения данной функции у=ƒ(х), ее заменяют многочленом Рn(х) степени n, значения которого всегда и легко вычисляемы. Обоснование возможности представлять функцию многочленом дает формула Тейлора.
26.1. Формула Тейлора для многочлена
Пусть функция ƒ(х) есть многочлен Рn(х) степени n:
ƒ(х)=Рn(х)=а0+а1х+а2х2+...+аnхn.
Преобразуем этот многочлен также в многочлен степени n относительно разности х-х0, где х0 — произвольное число, т. е. представим Рn(х) в виде
Рn(х)=А0+A1(x-х0)+А2(х-х0)2+...+Аn(х-х0)n (26.1)
Для нахождения коэффициентов А0, А1 ,..., Аn продифференцируем n раз равенство (26.1):
Р'n(х)=А1+2А2(х-x0)+3A3(x-x0)2+...+nAn(x-x0)n-1,
Рn''(х)=2А2+2•3А3(х-х0)+...+n(n-1)Аn(х-х0)n-2,
Рn"'(х)=2•3А3+2•3•4А4(х-х0)+...+n(n-1)(n-2)Аn(х-х0)n-3,
- - - - - - - - - - - - - - - - - -
Рn(n)(х)=n(n-1)( n-2)...2•1Аn
Подставляя х=х0 в полученные равенства и равенство (26.1), имеем:

Подставляя найденные значения A0,A1,...,An в равенство (26.1), получим разложение многочлена n-й степени Рn(х) по степеням (х-х0):
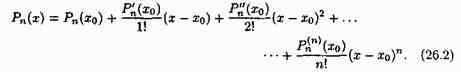
Формула (26.2) называется формулой Тейлора для многочлена Рn(х) степени n.
<< Пример 26.1
Разложить многочлен Р(х)=-4х3+3х2-2х+1 по степеням х+1.

Решение: Здесь х0=-1, Р'(х)=-12х2+6х-2, Р"(х)=-24х+6, Р'"(х)=-24. Поэтому Р(-1)=10, Р'(-1)=-20, Р"(-1)=30, Р'"(-1)=-24. Следовательно,
![]()
т. е. -4х3+3х2-2х+1=10-20(х+1)+15(х+1)2-4(х+1)3.
