Билет №1

Условная вероятность. Зависимые и независимые события. Теоремы умножения вероятностей

Событие А – независимо от события В, если вероятность А не зависит произошло В или нет. Событие А – зависимо от В, если вероятность А меняется в зависимости произошло В или нет.

Вероятность А вычисленное при условии, что произошло В называется условной вероятностью события А и обозначается: Р(А/В) Рв(А)

Теорема умножения вероятностей независимых событий: Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

P(AB)=P(A) ·P(B);

P(A₁,A_2….A_n)=P(A₁) ·P(A₂) ·..·P(A_n);

Биномиальное распределение вероятностей дискретных СВ

Опр. Говорят,что дискретные случайные величина имеет биномиальное распределное распределение, если возможное значение 0,1,2,…,n

P_k(P(x=k) =

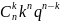
На практике биномиальное распределения показывает, когда пр-ся n-независимых опытов в каждом из которых событие А появляется с вероятностью Р.

Биномиальный закон зависит от двух параметров, найдем биномиальные характеристики от двух параметров.

n=2 p

x 0 1 2

p 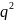2pq p²

M(x)= 0*q²+1*2*p*q+2*p²-2*p

Найдем дисперсию

D(x)=M(x²)-(M(x))²=2p(p+1)-4p²=[M(x²)=0²*q²+1²*2pq+2²*p²]=2p(1-p)=2pq

В случае n=2 M(x)=2p; D(x)=2pq

N=3 x 0 1 2 3

P q³ 3q²p 3qp² p³

M(x)=3p

D(x)=3pq

Для биномиального закона

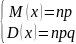
Интервальные оценки Доверительный интервал

Интервальное оценивание — один из видов статистического оценивания, предполагающий построение интервала, в котором с некоторой вероятностью находится истинное значение оцениваемого параметра.

Определение:

Пусть - неизвестный параметр генеральной совокупности. По сделанной выборке по определенным правилам находятся числа 1 и 2 такие чтобы выполнялось неравенство:

Интервал является доверительным интервалом для параметра 0, а число - доверительной вероятностью или надежностью сделанной оценки. Обычно надежность задается заранее, причем выбираются числа близкие к 1 (0.95, 0.99 или 0.999).

Доверительный интервал — это интервал, построенный с помощью случайной выборки из распределения с неизвестным параметром, такой, что он содержит данный параметр с заданной вероятностью.

Определение :

Пусть X1..Xn- выборка из некоторого распределения с плотностью , зависящей от параметра 0 , который может изменяться в интервале . Пусть - некоторая статистика и - функция распределения случайной величины , когда выборка имеет распределение с плотностью . Предположим, что есть убывающая функция от параметра . Обозначим квантиль распределения , тогда есть возрастающая функция от . Зафиксируем близкое к нулю положительное число (например, 0,05 или 0,01). Пусть . При каждом 0 неравенства (1)

выполняются с вероятностью -1 , близкой к единице. Перепишем неравенства (1) в другом виде: (2)

Обозначим , и запишем (2) в следующем виде:

Интервал называется доверительным интервалом для параметра 0, а вероятность - доверительной вероятностью.

Уровень значимости статистического теста — допустимая для данной задачи вероятность ошибки первого рода (ложноположительного решения, false positive), то есть вероятность отклонить нулевую гипотезу, когда на самом деле она верна.

В стандартной методике проверки статистических гипотез уровень значимости фиксируется заранее, до того, как становится известной выборка .

Чрезмерное уменьшение уровня значимости может привести к увеличению вероятности ошибки второго рода, то есть вероятности принять нулевую гипотезу, когда на самом деле она не верна. Вероятность ошибки второго рода связана с мощностью критерия простым соотношением . Выбор уровня значимости требует компромисса между значимостью и мощностью или (что то же самое, но другими словами) между вероятностями ошибок первого и второго рода.

Обычно рекомендуется выбирать уровень значимости из априорных соображений. Однако на практике не вполне ясно, какими именно соображениями надо руководствоваться, и выбор часто сводится к назначению одного из популярных вариантов . В докомпьютерную эпоху эта стандартизация позволяла сократить объём справочных статистических таблиц. Теперь нет никаких специальных причин для выбора именно этих значений.

Билет №2

Формула Байеса

Если событие A происходит с гипотезами Н₁,Н₂,…,H_n и если событие А уже произошло, то можно опред. Вероятности гипотез после проведения опыта.

Теор: пусть событие А может наступить при появлении одного из несовместных событий Н₁,Н₂,…,H_n которое образует группу событий. Если А уже произошло, то вероятность гипотезы H_i может определиться по формуле Баейса:

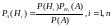
Док: будем искать вероятности: 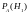, , например найдём по формуле Р(АН₁)=Р(Н₁)Р_Н1(А)=Р(А)Р_А(Н₁)

следовательно найдём

Формула позволяет переоценить вероятности гипотез после того как произошло событие А.

Локальная и интегральная теоремы Муавра-Лапласа

Локальная.

Пусть вероятность А в n-независимых испытаний равна р(0<p<1), тогда вероятность P_n(K) определяется по формуле:

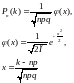
-чётная

Интегральная.

Вероятность того что в n-испытаниях событие А, р(0<p<1). Событие наступит не менее к₁ раз и не более к₂ раз определяется по формуле:

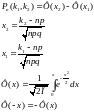
Доверительный интервал для математического ожидания при известном

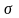
Пусть количественный Х генеральной совокупности признак распределен нормально , причем среднее квадратичное отклонение этого распределения известно. Требуется оценить неизвестное математическое ожидание 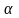по выборочной средней . Найдем доверительные интервалы покрывающие параметр с точностью .

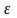Будем рассматривать выборочную среднюю как случайную величину 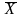и выборочные значения признака x₁,x₂,…,x_n - как одинаково распределенные независимые случайные величины X₁,X₂,…,X_n.

Если случайная величины Х распределена нормальна , то выборочная средняя ,

найденная по независимым наблюдениям , также распределена нормально. Параметры распределения таковы

М( )= , ( )= /

Должно выполняться соотношение

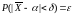
Пользуясь формулой вычисления вероятности заданного отклонения

заменив Х на и на ( )= / получаем

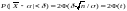
где

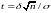
Из последнего равенства получаем 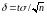можно записать

Приняв во внимание ,что вероятность Р задана и ровна , окончательно имеем

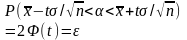
Смысл полученного такой : с точностью можно утверждать , что доверительный интервал 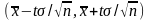покрывает н

Билет 3

Формула полной вероятности

Вероятность события А, которое может наступить при условии появления одного из несовместных событий Н₁,Н₂,…,H_n образующие полную группу событий равна сумме произведений вероятностей этих событий на соотв. вероятность события А:

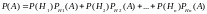
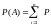
Доказательство: События Н₁,Н₂,…,H_n образуют полную группу. Их сумма есть достоверное событие: Н₁ +Н₂+…+H_n = по условию А – может произойти с событием H_i, т.е. произойдёт одно из АН₁,АН₂,…,АH_n

А=АН₁+АН₂+…+АН_N, тогда Р(А)=Р(АН₁+АН₂+…+АН_n) =несовместные=Р(АН₁)+Р(АН₂)+…+Р(АН_n)=события зависимые=Р(Н₁)Р_H1(А)+..+P(H_n)P_Hn(A)

Нормальное распределение вероятностей непрерывных СВ.

Опр.: Говорят, что НСВ распределена по норм. Закону с параметрами а,σ, если плотность распределения имеет вид:

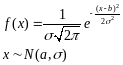
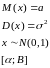
Вероятность попадания СВ в интервал [α,B]: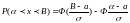

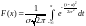- нормальный закон распределения

Полигон и гистограмма

Для наглядности строят различные графики статистического распределения.

По данным дискретного вариационного ряда строят полигон частот или относительных частот.

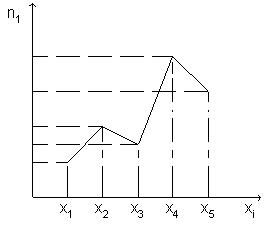
Полигоном частот называют ломанную, отрезки которой соединяют точки (x1; n1), (x2; n2), ..., (xk;nk). Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат - соответствующие им частоты ni. Точки ( xi; ni) соединяют отрезками прямых и получают полигон частот (Рис. 1).

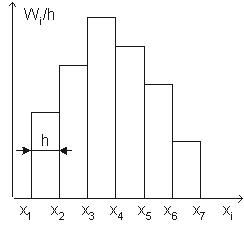
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению Wi / h (плотность относительной частоты).

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии Wi / h (Рис. 2).

Билет 4

Схема независимых испытаний Бернулли. Формула Бернулли

Если производится несколько испытаний причём вероятность события А в каждом испытании независит от исходов др. испытаний, то такие испытания называются независимыми относительно А. Например: бросание игральной кости.

Теор: вероятность того что в n-независимых испытаниях в каждом из которых вероятность появления события равна р(0<р<1) событие наступит ровно к раз безразлично в какой последовательности, определятся по формуле

Д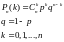 ок: в формуле подразумевается что А появится к-раз безразлично в какой последовательности, вероятность сложного события, что А наступит к раз, и не наступит n-k раз определяется по формуле: 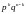, но таких испытаний может быть несколько, а именно события эти несовместны.

Нормальное распределение вероятностей непрерывных СВ.

Опр.: Говорят, что НСВ распределена по норм. Закону с параметрами а,σ, если плотность распределения имеет вид:

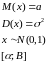
Вероятность попадания СВ в интервал [α,B]:

Правило 3-х сигм.

Если СВ , тогда справедлива формула:

Состоятельность несмещенность и эффективность оценок

Состоятельность характеризует сходимость по вероятности оценки q к истинному значению параметра T при неограниченном увеличении объема выборки n. Для состоятельности оценки достаточно, но не обязательно, чтобы математическое ожидание квадрата отклонения оценки от параметра M(T – q )2 стремилось к нулю с увеличением объема выборки (здесь и далее символ М означает математическое ожидание).

Несмещенность характеризует отсутствие систематических (в среднем) отклонений оценки от параметра при любом конечном, в том числе и малом, объеме выборки, т. е. M(q ) =T. Использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, приводит к систематическим ошибкам. Эффективность характеризует разброс случайных значений оценки около истинного значения параметраДля многих применяемых способов оценивания выборочные распределения параметров асимптотически нормальны, поэтому часто мерой эффективности служит дисперсия оценки. В таком понимании эффективная оценка – это оценка с минимальной дисперсией.

Билет 5.

1. Классическое, геометрическое, аксиоматическое и статистическое определение вероятностей.

Вероятность события – математическая оценка возможности появление случайного события в результате опыта.

Если m- число событий благоприятствующих событию A, то

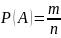
Свойство вероятностей события А:

1.

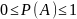
2.

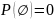
3.

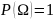
4. А,В – несовместные P(A+B)=P(A)+P(B)

Пусть происходит эксперимент и событие А появляется в М из N, тогда 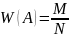– относительная частота события.

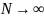- остаётся примерно постоянным.

Статистическое определение вероятности заключается в том что за вероятность события А принимается её относительная частота.

Аксиоматическое определение вероятности: вероятность события А это функция Р(А) удовлетворяющая след. свойствам:

1. P(∅)=0

2. P(Ω)=1

3. 0≤P(A)≤1

4. Ai – несовместное событие i=1,..,n то

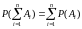
_{Геометрическое определение}

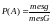
Показательное распределении вероятностей непрерывных СВ. Функция надежности.

Опр.: Говорят, что НСВ имеет покозат. (экспонентц.) распределение, если плотность вероятностей имеет вид:

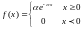
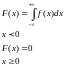
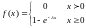
Найдем математические характеристики:

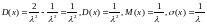
_{Функция надежности.}

_{функция распределения F(t)=P(T<t)=1- e-mt определяет вероятность отказа устройства за время t.}

_{Найдем вероятность противоположного события- безотказной работы за время t:}

_{Функция R(t) называется функцией надежности. Выясним смысл числовых характеристик и параметра распределения.}

_{Математическое ожидание - это среднее время между двумя ближайшими отказами устройства, а величина обратная математическому ожиданию (параметр распределения)- интенсивность отказов, т.е. количество отказов в единицу времени.}

3.Проверка гипотезы о нормальном распределении генеральной совокупности.Критерий согласия.

Проверка гипотезы о предполагаемом законе неизвестного распределения производится при помощи специально подобранной случайной величины – критерия согласия.

Критерий согласия (хи-квадрат)

Критерий согласия разработан лучше других критериев и чаще других используется. Он основан на сравнении эмпирических частот интервалов группировки с теоретическими (ожидаемыми) частотами, рассчитываемыми по формулам нормального распределения.

Порядок, применения:

1. Формулируется гипотеза, выбирается уровень значимости a.

2. Получается выборка объема n 40 независимых наблюдений и представляется эмпирическое распределение в виде интервального вариационного ряда.

3. Рассчитываются выборочные характеристики и S.

4. Вычисляются значения теоретических частот :

где Ф0(u) — функции Лапласа, xвi и хнi — верхняя и нижняя границы i-го интервала группировки.

5. Соответственно складываются и эмпирические частоты объединяемых интервалов.

5. Значение -критерия рассчитывается по формуле:

где ni — эмпирические частоты; – ожидаемые (теоретические) частоты; k — число интервалов группировки после объединения.

6. Из таблиц распределения находится критическое значение критерия для уровня значимости а и числа степеней свободы n=n–3.

7. Вывод: если то эмпирическое распределение не соответствует нормальному распределению на уровне значимости a, в противном случае нет оснований отрицать это соответствие.

_{Билет 6}

Повторение испытаний

Если производится некоторое количество испытаний, в результате которых может произойти или не произойти событие А, и вероятность появления этого события в каждом из испытаний не зависит от результатов остальных испытаний, то такие испытания называются независимыми относительно события А.

Если в результате п опытов событие А наступает ровно т раз, то остальные п-т раз это событие не наступает. Событие А может появиться т раз в п испытаниях в различных комбинациях, число которых равно количеству сочетаний из п элементов по т. Это количество сочетаний находится по формуле:

6.1.2. Распределение Пуассона

Говорят,что случайная величина распределена по закону Пуассона,если ее возможное значение 0,1,2,…,л… а соответственные вероятности определяться по формуле P_k=P_n(x=k)= , k=0,1,2,…

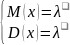
Системы 2-х СВ и законы их распределения

Примеры: 1) на пл-ти(x,y) –двумерная СВ

Наиб. распр-ным распределением дискр. величины явл. таблица

xi\yj	x1	x2	…	xn
y1	p11	p12	…	p1n
y2	p21	p22	…	p2n
…	…	…	…	…
ym	pm1	pm2	…	pmn

События (x=x_i,y=y_j), где i=1,n‾, j=1,m‾ образуют полную группу событий, сумма вероятностей =1

Свойства функции распределения.

1) 0 ≤ F(x, y) ≤ 1 (так как F(x, y) является вероятностью).

2) F(x, y) есть неубывающая функция по каждому аргументу:

F(x2, y) ≥ F(x1, y), если x2 > x1;

F(x, y2) ≥ F(x, y1), если y2 > y1.

Метод моментов для оценки неизвестных параметров распределения

Метод моментов

выбирается столько эмпирических моментов, сколько требуется оценить неизвестных параметров распределения. Желательно применять моменты младших порядков, так как погрешности вычисления оценок резко возрастают с увеличением порядка момента;

вычисленные по ЭД оценки моментов приравниваются к теоретическим моментам;

параметры распределения определяются через моменты, и составляются уравнения, выражающие зависимость параметров от моментов, в результате получается система уравнений. Решение этой системы дает оценки параметров распределения генеральной совокупности.

Билет №7