
- •2)Сходящ. Послед.Имеет только 1 предел
- •3)Сходящ. Послед.Ограничена
- •5. Предел ф-ции при X . Св-ва предела ф-ции.
- •11.Понятие дифференцируемости функции в точке. Диф. Функция. Таблица дифференциалов.
- •16. Неопределенный интеграл. Множество всех первообразных функций f(X) называется неопределенным интегралом функции f(X) и обозначается .
- •18. Таблица интегралов.Интег-ниерац-ных и иррац-ных функций.
- •33. Уравнение Бернулли. Дифференциальные уравнения в полных дифференциалах.
- •35. Метод Эйлера решения диф.Ур.
33. Уравнение Бернулли. Дифференциальные уравнения в полных дифференциалах.
Решением
линейное неоднородного уравнение
y`+p(х)у=q(x)
(7)
Решение будем искать в виде:
у=C(x) (8)
(8)
Где
C(x)-
неизвестная функция подставляя (8) и
(7), имеем:
С (х)
+С(х)
+С(х)р(х)
=q(x)
(х)
+С(х)
+С(х)р(х)
=q(x)
С(х)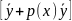 =0
=0
Значит,
С
(х)
=q(x)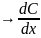 =
=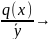 C(x)=
C(x)=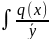 dx+C
dx+C
Подставляя
найденное С(х) в (8), получим формулу
Бернулли y=C
+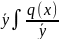 dx
dx
Описанный метод решения уравнения (7) наз. методом вариации произвольной постоянной или методом методом Лагранжа. Др. методом решения линейного уравнения явл метод Бернулли , кот. заключается в след.:
Решение уравнения(7) ищем в виде y=uv, где u(x) и v(x)- непрерывно дифференцинцируемые на I функции, причём u(x) 0, v(x) 0.
После
подстановки y
в (7) и учитывая, что
=
u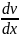 +v
+v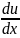
Получим u +v +p(x)uv=q(x)(9)
Потребуем, чтобы v( +p(x)u)=0 , будем иметь
+p(x)u=0 (10)
Или
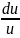 =
p(x)dx.
Подставляя частное решение этого
уравнения u=
=
p(x)dx.
Подставляя частное решение этого
уравнения u=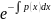 в (9), с учётом (10) получим dv=
q(x)dx,
а v=
в (9), с учётом (10) получим dv=
q(x)dx,
а v=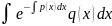
+C.
Окончательно, y=
Уравнением
Бернулли наз. нелинейноедиф. Уравнение
первого порядка вида: y`+p(x)y=q(x)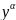 (11)
(11)
Где
α(α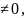 α
1)
– произвольное вещественное число
подстановка u=
α
1)
– произвольное вещественное число
подстановка u=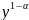 приводит уравнение (11) к линейному
неоднородному уравнению. Уравнение(11)
можно решать также подстановкой
y(x)=u(x)v(x).
Тогда, записав уравнение(11) в виде
u`v+(v`+p(x)v)u=q(x)
приводит уравнение (11) к линейному
неоднородному уравнению. Уравнение(11)
можно решать также подстановкой
y(x)=u(x)v(x).
Тогда, записав уравнение(11) в виде
u`v+(v`+p(x)v)u=q(x)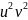 ,
решим два уравнения с разделяющимися
переменными: v`+p(x)v=0(берём
только 1 решение v
0)
и u`=q(x)
(берём
его общее решение)
,
решим два уравнения с разделяющимися
переменными: v`+p(x)v=0(берём
только 1 решение v
0)
и u`=q(x)
(берём
его общее решение)
Подставляя найденные u и v в соотношение y(x)=u(x)v(x), получим общее решение уравнения Бернулли.
Уравнение вида: P(x,y)dx+Q(x,y)dy=0(12) наз уравнением в полных дивверенциалах, если его левая часть явл полным дифференциалом некоторой функции u ,т.е.
P(x,y)dx+Q(x,y)dy=du(x,y)(13)
34.Диф ур-ния высших порядков.Метод Эйлера.
Диф.урав
n-ого порядканаз.урав.вида f(х, y,
y…’,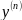 )=0.Решением
такого урав.служит всякая,
)=0.Решением
такого урав.служит всякая,
n
раз непрерывно диф.ф-ция y=
(х),опред.на
некатором интервале(а,b) и обращ.данное
урав.втождество.Урав.Ф(х,y,С1,С2…С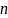 )=0
определяющ. Общее решение как неявную
ф-цию,наз.общим интегралом диф.урав.Линейным
однород.урав.n-ого порядка с постоян.коэфиц.
наз. урав
)=0
определяющ. Общее решение как неявную
ф-цию,наз.общим интегралом диф.урав.Линейным
однород.урав.n-ого порядка с постоян.коэфиц.
наз. урав +а1
+а1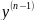 +а2
+а2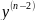 +…+
+…+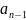 y’+
y’+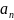 y=0
y=0
y=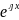 ,
,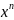 +а1
+а1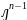 +…+
ԓ+
=0
это урав.наз. характеристическим .
Решен.однородного диф.урав.
+…+
ԓ+
=0
это урав.наз. характеристическим .
Решен.однородного диф.урав.
свелось к решен.алгебраич. урав.,этот м-д наз.м-дом Эйера.
35. Метод Эйлера решения диф.Ур.
Пусть λ1, λ2, λ3,…, λn –корни ур-ния λn+a1 λn-1+…+an-1 λ+an=0 (3),причем среди них могут быть и кратные(повторяющиеся).Возм.след.случаи:
1) λ1, λ2, λ3,…, λn-вещественные и различные.Тогда фундаментальная система реш. ур-нияy(n)+a1y(n-1)+a2y(n-2)+…+an-1y`+any=0 (1) имеет вид: еλ1х, еλ2х, …, еλnх (4),а общ.решениемэт.ур-ния будет: Ў=С1еλ1х+С2 еλ2х+…+Сnеλnх. где С1,С2,…,Сn-произвольные постоянные.
2) Корни характеристического ур-ния вещественные, но среди них есть кратные.Пусть,например, λ1=λ2=…= λк, т.е. λ1 явл. к-кратным корнем ур-ния (3),а все ост. (n-k) корней различные.Фундаментальнаясист. решений ур-ния (1)в эт.случ.: еλ1х, хеλ1х, …,хк-1 еλ1х, еλк+1х, еλnх, (5),а общ.реш. Ў=С1еλ1х+С2х еλ1х+…+ Скхк-1еλ1х + Ск+1 еλл+1х +Сnеλnх.
3) Среди хар-ого ур. (3)есть комплексные. Пусть для определенности λ1=α+iβ, λ2=α-iβ, λ3=υ+iδ,λ4=υ-iδ,а ост.корни вещественные и различные.Поскольку коэффициенты ai, i=от 1до n, ур-ния (3)вещественные,то комплексные корни этого ур-ния попарно сопряженные.Согласно у=еλх (2) будем иметь: у1= еλ1х=е(α+iβ)х=eαx(cosβx+isinβx), у2=eαx(cosβx-isinβx), у3=eυx(cosδx+isinδx), у4=eυx(cosδx-isinδx), у5=eλ5x,…, уn=eλnx.Фунд.сист.реш.:еαхcosβx,еαхsinβx,еυхcosδx,еυхsinδx,eλ5x,…,eλnx, (6). Ў=С1еλхcosβ+С2 еλхsinβ+C3еυхcosδx+C4 еυхsinδx +C5 eλ5x +Cnеλnх .Общ.реш.
4) Пусть λ1=α+iβявл. к-кратнымкорнемур.(3 ) (к<=n\2), λ2=α-iβ также будет к-кратн.корнем и пусть ост.корнивеществ.и различны. Фунд.сист.реш.ур.(1): еαхcosβx,еαхsinβx,хеλхcosβx,хеλхsinβx,…,хк-1еλхcosβx, хк-1еλхsinβx, еλ2к+1х,…,eλnx (7). Общ.реш.диф.ур.1 запишется: Ў=С1еαхcosβx+С2еαхsinβx+С3хеλхcosβx+С4хеλхsinβx,…,С2к-1хк-1еλхcosβx+C2kхк-1еλхsinβx+С2к+1еλ2k+1х+…+Cneλnx
