
- •2)Сходящ. Послед.Имеет только 1 предел
- •3)Сходящ. Послед.Ограничена
- •5. Предел ф-ции при X . Св-ва предела ф-ции.
- •11.Понятие дифференцируемости функции в точке. Диф. Функция. Таблица дифференциалов.
- •16. Неопределенный интеграл. Множество всех первообразных функций f(X) называется неопределенным интегралом функции f(X) и обозначается .
- •18. Таблица интегралов.Интег-ниерац-ных и иррац-ных функций.
- •33. Уравнение Бернулли. Дифференциальные уравнения в полных дифференциалах.
- •35. Метод Эйлера решения диф.Ур.
16. Неопределенный интеграл. Множество всех первообразных функций f(X) называется неопределенным интегралом функции f(X) и обозначается .
Функция f(x) называется подынтегральной функцией, f(x)dx – подынтегральное выражение, переменная х – переменная интегрирования.
Итак, если F(х) – первообразная функции f(х) на промежутке X, то интеграл .
Подчеркнем, что символ обозначает совокупность всех первообразных для функции f(x). Отыскание неопределенного интеграла по известной подынтегральной функции называется интегрированием этой функции.
Свойства неопределенного интеграла:
1) Если функция f дифференцируема на некотором промежутке, то на нем выполняется: или ;
2) Пусть функция f(x) имеет первообразную на некотором промежутке I, тогда для всех х из промежутка I выполняется равенство: ;
3) Если ф-ция f имеет первообразную на промежутке I и k – число, но ф-ция также имеет на промежутке I первообразную, причем при справедливо равенство: ;
4) Неопределенный интеграл от суммы двух ф-ций равен сумме интегралов от этих ф-ций: .
17.Метод замены переменной. Под знаком интеграла может оказаться функция, для которой нет табличного интеграла и непосредственное интегрированиеневозможно. В таком случае используют другие приёмы в частности, метод замены переменной. Утв.1:Пусть функция х=φ(t) определена и дифференцируема на промежутке T,а Х-множество её значений. Пусть функция у=f(x) определена на множества Х и имеет на этом промеж.первообразную, тогда справедливо формула:
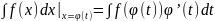 ,
которая наз.формулой замены переменной
в неопределённом интеграле.
,
которая наз.формулой замены переменной
в неопределённом интеграле.
Интегрир. по частям
Утверждение2:Пусть
функции u=u(x)
и v=v(x),
дифферен. на промежутке Х и пусть
существ. .
Тогда существ.
.
Тогда существ.
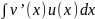 И
справедливо формула 2:
И
справедливо формула 2:
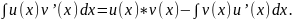
Таблица интегралов:
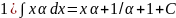
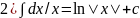
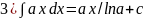
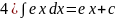
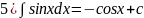
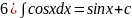
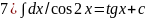
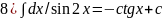
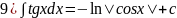

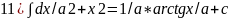
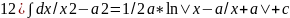
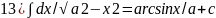
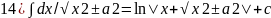
18. Таблица интегралов.Интег-ниерац-ных и иррац-ных функций.
Интегрирование рац ф-ций. Определение: Элементарными называются дроби следующих четырех типов:
I.
1/ax+b II. 1/ (ax +b)m
III. Mx+N/(ax2+bx+c) IV. Mx+N/(ax2+bx+c)
nm,
n – натуральные числа (m ≥ 2, n ≥ 2) и b2 –
4ac <0. Первые два типа интегралов от
элементарных дробей довольно просто
приводятся к табличным подстановкой t
= ax + b. 1)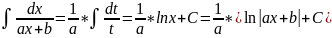 .
.
2)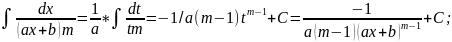
Интегрирование рациональных дробей : Для того, чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби. Теорема: Если R(x)=Q(x)/P(x) = - правильная рациональная дробь, знаменатель P(x) которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: P(x) = (x - a)α…(x - b)β(x2 + px + q)λ…(x2 + rx + s)μ), то эта дробь может быть разложена на элементарные по следующей схеме: где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины. При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин Ai, Bi, Mi, Ni, Ri, Si применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х. Применение этого метода рассмотрим на конкретном примере.
Таблица:1)∫хαdx=xα+1/α+1+C;2)∫dx/x=ln|x|+c;3)∫axdx=ax/lna+c;4)∫exdx=ex+c;5)∫sinxdx=-cosx+c;
6)∫cosxdx=sinx+c;7)∫dx/cos2x=tgx+c;8)∫dx/sin2x=-ctgx+c;9) ∫tgxdx=-ln|cosx|+c;
10) ∫ctgxdx=ln|sinx|+c;11) ∫dx/a2+x2=1/a*arctgx/a+c;12) ∫dx/x2-a2=1/2a*ln|x-a/x+a|+c;
13) ∫dx/√a2-x2=arcsinx/a+c;14)∫dx/√x2±a2=ln|x+√x2±a2|+c.
19. Интегралы с квадратичной иррациональностью
1)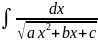 ,где
а≠0.Путём дополнения квадратного
трёхчлена
,где
а≠0.Путём дополнения квадратного
трёхчлена
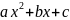 до полного квадрата,приводится в
зависимости от знака aк
одному из табличных интегралов.
до полного квадрата,приводится в
зависимости от знака aк
одному из табличных интегралов.
2)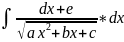 ,где
ad≠0.
Можно привести к интегралу (9):
=
,где
ad≠0.
Можно привести к интегралу (9):
=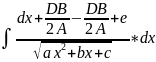 =
=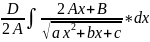 +
+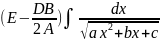 =
=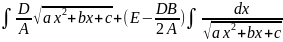
3)Вычислим
интеграл: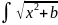 *dx,b>0,
*dx,b>0,
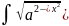 *dx,a≠0
(10)
*dx,a≠0
(10)
*dx=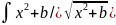 =
=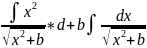 (11). Выч. Интеграл
(11). Выч. Интеграл
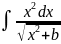 по частям. Пологая u=x,
du=
по частям. Пологая u=x,
du= ,
тогда du=dx,
v=
,
тогда du=dx,
v=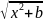 ,
тогда получим
=x
,
тогда получим
=x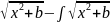 *dx.
Подставляя в последнее выражение в ф-лу
(11) 2
*dx.
Подставляя в последнее выражение в ф-лу
(11) 2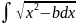 =x
+b
=x
+b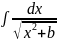 ,
,
Интегрирование тригонометрических функции и дифференциального бинома.
1)Интегралы
от квадратов и других чётных степеней
синуса и косинуса находят,применяя
следующие ф-лы понижения степени: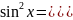 ;
;

2)Интегралы от кубов и других нечётных степеней синуса и косинуса находят,отделяя от нечётной степени один множитель и пологая кофункцию равной новой переменной u.
Интеграл
ʃ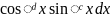 находятся по правилу 1), если d
и c
оба чётные и по правилу 2), если d
и c
нечётно.
находятся по правилу 1), если d
и c
оба чётные и по правилу 2), если d
и c
нечётно.
20.Определение
определённого интеграла. Основные
свойства определённого интеграла.Предел
от суммы
![]() при
при
![]() , если он существует и конечен, называется
определенным интегралом от функции
f(x)
в пределах от a
до b
и обозначается:
, если он существует и конечен, называется
определенным интегралом от функции
f(x)
в пределах от a
до b
и обозначается:![]() Если
существует определенный интеграл от
функции f(x)
, то в этом случае функция называется
интегрируемой на отрезке [a,b]
.Определенный интеграл от непрерывной
функции равен разности значений
первообразной функции при верхнем и
нижнем пределах.
Если
существует определенный интеграл от
функции f(x)
, то в этом случае функция называется
интегрируемой на отрезке [a,b]
.Определенный интеграл от непрерывной
функции равен разности значений
первообразной функции при верхнем и
нижнем пределах.![]()
Свойства:
![]()
![]()
![]()
![]()
21.Метод трапеций. Приложение определённого интеграла.
Пусть
задана ф.f(x)-
непрерывная на отрезке [a,b]
необходимо вычислить
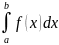 .
.
Разлбъём отрезок [a,b] на n- равных частичных отрезков точками A=x0<x1<…<xn=b
∆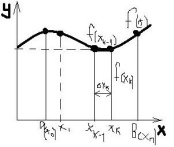 Xk=Xk-Xk-1=(b-a)/n,
k=1;n
Xk=Xk-Xk-1=(b-a)/n,
k=1;n
Проведя прямыеx= Xk, k=[0;n] всю криволинейную трапецию разобъём на n-частичных криволинейных трапеций.Соединим две соседние точки
( x(k-1); f(xk-1)), (x(k); f(xk)) хордой и рассмотрим n прямоугольных трапеций.
Sk-той
трапеции равна
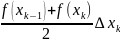 .
.
Исходя из геом. смысла опр. интеграла
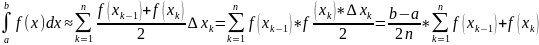 .
.
Пусть
yk=f(xk),
тогда
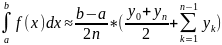 .
(5).
.
(5).
Для
наглядности на рисунке рассмотрена
неотрицательная непрерывная ф-ция.
Однако по формуле (5) имеет место для
любой интегрируемой на отрезке
[a,b]ф.f(x).Эта
формула наз.формулой трапеций.Она тем
точнее, чем больше число n.
В частности если ф.f(x)
имеет вторую непрерывную производную,
то абсолютная погрешность не превосходит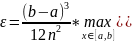 .
.
Приложение опр. интеграла
Из
геом смысла определенного интеграла
следует, что интервал от a,b
 ,численно равен Sкриволин.
трапеции ограниченной графиком y=f(x),
прямыми x=a,
x=b,
и осью абсцисс (в случае если ф-цияf(x)
неотрицательная)
,численно равен Sкриволин.
трапеции ограниченной графиком y=f(x),
прямыми x=a,
x=b,
и осью абсцисс (в случае если ф-цияf(x)
неотрицательная)
22.
Несобственные интегралыОпределённый
интеграл называется несобственным,
если выполняется, по крайней мере, одно
из следующих условий:1.Предел a или b (или
оба предела) являются бесконечными;
2.Функция f(x) имеет одну или несколько
точек разрыва внутри отрезка [a, b].Интеграл
![]() называется абсолютно сходящимся, если
называется абсолютно сходящимся, если![]() сходится. Если интеграл сходится
абсолютно, то он сходится.Интеграл
сходится. Если интеграл сходится
абсолютно, то он сходится.Интеграл
![]() называется условно сходящимся, если
сходится, а
называется условно сходящимся, если
сходится, а![]() расходится. Признак
Дирихле. Интеграл
расходится. Признак
Дирихле. Интеграл
![]() сходится, если: 1).функция
f(x) непрерывна и имеет ограниченную
первообразную на (a, b]; 2).функция g(x)
непрерывно дифференцируема и монотонна
на (a, b], причём.
сходится, если: 1).функция
f(x) непрерывна и имеет ограниченную
первообразную на (a, b]; 2).функция g(x)
непрерывно дифференцируема и монотонна
на (a, b], причём.![]() Признак
Абеля. Интеграл сходится, если: 1).функция
f(x) непрерывна на (a, b] и интеграл сходится;
2).функция g(x) ограничена, непрерывно
дифференцируема и монотонна на (a, b], то
есть имеет конечный предел:
Признак
Абеля. Интеграл сходится, если: 1).функция
f(x) непрерывна на (a, b] и интеграл сходится;
2).функция g(x) ограничена, непрерывно
дифференцируема и монотонна на (a, b], то
есть имеет конечный предел:
23.Понятие
числового ряда. Пусть {аn}-числовая
послед-ть, где аn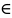 R,
n
N.
Выражение вида а1+а2+а3+…+аn+…=
R,
n
N.
Выражение вида а1+а2+а3+…+аn+…=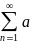 n
(1) наз.числовымрядом.Числа
а1,а2,…аnназ.членамиряда,а
аn-n-м
или общим членом ряда (1). Сумма первых
n-членов
ряда (1) наз. n-ой
частичной суммой данного ряда и обознач.
Sn:
Sn=
а1+а2+а3+…+аn=
n
(1) наз.числовымрядом.Числа
а1,а2,…аnназ.членамиряда,а
аn-n-м
или общим членом ряда (1). Сумма первых
n-членов
ряда (1) наз. n-ой
частичной суммой данного ряда и обознач.
Sn:
Sn=
а1+а2+а3+…+аn=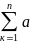 к.
Имеем S1=a1,
S2=a1+a2,
S3=a1
+a2+a3,
Sn=
а1+а2+а3+…+аn.
Рассм.послед-ть частичных сумм ряда (1)
S1
,S2
...,Sn.
Если послед-ть частичных сумм { Sn
} имеет конечный предел S,то
числовой ряд (1) наз.сходящимся,а число
S
наз. Суммой ряда (1): S=
к.
Имеем S1=a1,
S2=a1+a2,
S3=a1
+a2+a3,
Sn=
а1+а2+а3+…+аn.
Рассм.послед-ть частичных сумм ряда (1)
S1
,S2
...,Sn.
Если послед-ть частичных сумм { Sn
} имеет конечный предел S,то
числовой ряд (1) наз.сходящимся,а число
S
наз. Суммой ряда (1): S=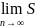 nили
nили
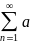 n.
Если же предел послед-ти{ Sn
} не существует или бесконечен,то ряд
(1) наз.расходящимся.Необход.условие
сходимости. Если ряд
nсходится,
то
n.
Если же предел послед-ти{ Sn
} не существует или бесконечен,то ряд
(1) наз.расходящимся.Необход.условие
сходимости. Если ряд
nсходится,
то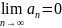 .
.
24. Критерии сходимости числового ряда.Осн. м-ды исследования знакопол. ряда. Теорема 4: для того что бы ряд сходился,необходимо и достаточно что бы последовательность его частичных сумм была ограниченной.
Теорема
5: для сходимости ряда необходимо и
достаточно, что бы для любого ε>0существовалл
N(ε)
такой что при всяком натуральном р и
всех n>N(ε)
имело место неравенство │Sn+p-Sn│=│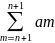 │<ε
│<ε
Сходимость или расходимость знакоположительного ряда часто можно установить путём сравнения его с другими рядами, о которых известно сходятся они или нет.
Теорема
6:пусть даны два ряда с неотриц. членами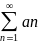 (обозначимА)и
(обозначимА)и
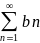 ( обозначим В) и пусть an≤bnтогда
из сходимости ряда В следует сходимость
ряда А, а из расходимости ряда А
расходимость ряда В.
( обозначим В) и пусть an≤bnтогда
из сходимости ряда В следует сходимость
ряда А, а из расходимости ряда А
расходимость ряда В.
Теорема
7: пусть даны два знакоположительных
ряда А и В если сущ. Конечный отличный
от нуля предел
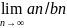 =A
(0<А<∞), то ряды А и В одновременно
сходятся или расходятся.
=A
(0<А<∞), то ряды А и В одновременно
сходятся или расходятся.
Теорема
8: пусть дан ряд
с положительными членами и сущ предел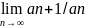 =q
тогда при q<1
ряд сходится а при q>1
расходится.
=q
тогда при q<1
ряд сходится а при q>1
расходится.
Теорема
9:если для ряда
с
неотриц членами сущ предел
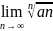 =q
то при q<1
ряд сходится ,а при q>1
расходится.
=q
то при q<1
ряд сходится ,а при q>1
расходится.
Теорема
10: если члены знакоположительного ряда
монотонно
убывают и сущ положительная невозрастающая
функция f(x)
такая что f(n)=an
при n≥1.
То ряд и несобственный интеграл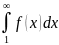 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
25.
Знакочередующиеся ряды. Абсолютная и
условная сходимость.Ряд
называется знакочередующимся, если его
члены попеременно принимают значения
противоположных знаков, т. е.:![]() Теорема Лейбница о сходимости
знакочередующихся рядов.Признак
Лейбница — признак сходимости
знакочередующегося ряда, установлен
Готфридом Лейбницем. Формулировка
теоремы:Пусть для знакочередующегося
ряда
выполняются
следующие условия:
Теорема Лейбница о сходимости
знакочередующихся рядов.Признак
Лейбница — признак сходимости
знакочередующегося ряда, установлен
Готфридом Лейбницем. Формулировка
теоремы:Пусть для знакочередующегося
ряда
выполняются
следующие условия:![]()
![]() тогда ряд сходится. Если, выполнены
все условия, и ряд из модулей сходится,
то исходный ряд сходится абсолютно.
Если выполнены все условия, но ряд из
модулей расходится, то исходный ряд
сходится условно. Строгая положительность
а-n
существенна. Ряды, удовлетворяющие
признаку Лейбница, называются рядами
Лейбница. Следует отметить, что этот
признак является достаточным, но не
необходимым
тогда ряд сходится. Если, выполнены
все условия, и ряд из модулей сходится,
то исходный ряд сходится абсолютно.
Если выполнены все условия, но ряд из
модулей расходится, то исходный ряд
сходится условно. Строгая положительность
а-n
существенна. Ряды, удовлетворяющие
признаку Лейбница, называются рядами
Лейбница. Следует отметить, что этот
признак является достаточным, но не
необходимым
26.
Знакопеременные ряды. Сходимость.Числовой
ряд
n,содер
бесконечное множество положит и бесконеч
множество отриц членов наз знакопеременным.
Теорема 1Пусть дан знакопеременный ряд
n(1).Если
сходится ряд
n(2)
составленный из модулей членов данного
ряда (1)сходится и знакопеременный
ряд(1).Опр.Ряд
(1)наз абсолютно сходящимся,если ряд
(2)сходится.Если же ряд(1)сходится,а
ряд(2)расходится,то ряд(1)наз условно
сходящимся.Св-ва абсолютно сходящихся
рядов:1).Если ряд(1)абсолютно сходится и
имеет сумму S,то ряд,полученный из него
перестановкой членов также сходится и
имеет ту же сумму S,что и исходный
ряд(1).2)Абсолютно сходящиеся ряды
nи
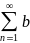 n
с суммами S1 и S2 можно почленно
складывать(вычислять).В итоге получится
абсолютно сход ряд,сумма которого равна
S1+S2,
(S1-S2).Опр.Произведение
2 рядов
nи
nназ
ряд вида(а1б1)+(а1б2+а2б1)+(а1б3+а2б2+а3б1)+…+(
а1бн+а2бн-1+…+анб1)+…Опр.
Произведение
2-х абсолютно сходящихся рядов с суммами
S1 и S2 есть бесконечно сход ряд,сумма
которого= S1*S2.Теорема
Римоно:Если ряд(1)сходится неабсолютна
,то какое бы ни взять число S,можно
так переставить члены в этом ряду,чтобы
преобразованный ряд имел своей суммой
именно S.
n
с суммами S1 и S2 можно почленно
складывать(вычислять).В итоге получится
абсолютно сход ряд,сумма которого равна
S1+S2,
(S1-S2).Опр.Произведение
2 рядов
nи
nназ
ряд вида(а1б1)+(а1б2+а2б1)+(а1б3+а2б2+а3б1)+…+(
а1бн+а2бн-1+…+анб1)+…Опр.
Произведение
2-х абсолютно сходящихся рядов с суммами
S1 и S2 есть бесконечно сход ряд,сумма
которого= S1*S2.Теорема
Римоно:Если ряд(1)сходится неабсолютна
,то какое бы ни взять число S,можно
так переставить члены в этом ряду,чтобы
преобразованный ряд имел своей суммой
именно S.
27.
Степенные ряды. Сходимость степенного
ряда. Опр.
Функциональный
ряд вида
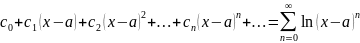 ,(1), где
,(1), где
 ,
,
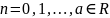 ,
наз-ся степенным рядом. Числа
,
наз-ся степенным рядом. Числа
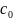 ,
,
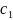 ,
…,
,
…,
 ,
… наз-ся коэффициентами степенного
ряда (1). Если
,
… наз-ся коэффициентами степенного
ряда (1). Если
 ,
то ряд (1) имеет вид
,
то ряд (1) имеет вид
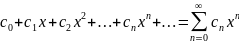 ,
(2). Будем рассматривать только такие
степенные ряды, т.к. полагая в (1)
,
(2). Будем рассматривать только такие
степенные ряды, т.к. полагая в (1)
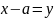 ,
получаем ряд вида (2).
,
получаем ряд вида (2).
Степенной ряд (2) всегда сходится в точке х=0. Если х≠0, то ряд (2) может сх-ся или расх-ся.
Т1 (Абеля). Если степенной ряд (2) сх-ся в т. х0≠0, то во всех точках х, |х|<|х0|, он схся абсолютно. Если в т. х1≠0 степ.ряд (2) расх-ся, то он расходится во всех точках х, |х|>|х1|.
Теор.
Абеля дает ясное представление об
области сходимости степенного ряда.
Для наглядности воспользуемся следующим
приемом: окрасим мысленно в зеленый
цвет каждую точку сходимости ряда (2), а
в красный цвет – каждую точку расходимости
ряда (2). Очевидно, что т. х=0 будет всегда
окрашена в зеленый цвет. Если степенной
ряд сходится всюду на R,
то вся числовая ось будет зеленой. Если
степ.ряд везде расходится, то вся числовая
ось, кроме т. х=0, будет красной. Если
какая-нибудь точка х0≠0
будет окрашена в зеленый, то зелеными
будут все точки лежащие между х0
их=0,
а также между -х0
их=0.
Если какая либо точка х1>0
будет красной, то будут красными все
точки лежащие правее х1.
Если х1<0
будет красной, то будут красными все
точки лежащие левее х1.
Т.к. каждая точка числовой оси будет
либо зел. либо красн., то идя от т. х=0
вправо по числовой оси сначала будем
встречать только зел. точки, а затем –
только красные, причем граничная или
разделяющая эти разноцветные участки
точка R
может быть как красн., так и зел. цвета
(в зависимости от того сходится ряд на
границе или расх.) То же самое можно
сказать, если идти налево от точки х=0 в
частности в т. х=-R
ряд может сходиться или расх-ся.
![]()
Опр. Число Rназ-ся радиусом сходимости ряда (2), интервалом (-R,R) – интервалом сходимости. Если ряд (2) сх-ся только в т. х=0, то R=0; если ряд сх-ся для всех х R, то R=+∞.
Подчеркнем, что в кажд. т. х (-R,R) ряд (2) будет сх-ся абсолютно, в точках х=±R может сх-ся или расх-ся.
Т2Если
сущ-ет предел
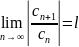 ,
то радиус сходимости R
ряда (2) равен
,
то радиус сходимости R
ряда (2) равен
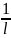 , т.е.
, т.е.
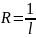 .
.
Т3Если
сущ-ет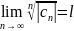 ,
то
.
,
то
.
Сформулируем основные свойства степенных рядов (2) с интервалом сходимости (-R;R):
1. Степенной ряд (2) сх-ся равномерно на любом отрезке, содержащемся в (-R;R).
2. Сумма S(x) степенного ряда (2) явл-ся непрерывной ф-цией в интервале сходимости (-R;R).
3.
Ст. ряды
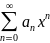 и
и
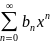 , имеющие радиусы сход-сти соотв-но R1
и R2,
можно почленно складывать, вычитать и
умножать, причем радиус сходится
полученных т.о. рядов равен меньшему из
чисел R1
и R2.
, имеющие радиусы сход-сти соотв-но R1
и R2,
можно почленно складывать, вычитать и
умножать, причем радиус сходится
полученных т.о. рядов равен меньшему из
чисел R1
и R2.
4. Ст. ряд (2) внутри интервала сх-сти (-R;R) можно почленно дифференцировать.
5. Ст. ряд (2) можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сх-сти (-R;R).
Отметим, что св-ва 1-5 справедливы и для ст. рядов вида (1).
28.Разложение
функций в степенные ряды. Ряд Тейлора.
Для любой функции f(х),
определённой в окрестности точки а и
имеющей в ней производные до (n+1)-ого
порядка включительно, справедлива
формула Тейлора: (1),
где
Rn(x)
– остаточный член формулы Тейлора.
(1),
где
Rn(x)
– остаточный член формулы Тейлора.
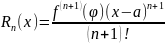 ,
,
 ,
,
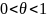 .
Соотношение (1) запишем в виде
.
Соотношение (1) запишем в виде
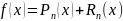 (2),
где Pn(x)
– многочлен Тейлора:
(2),
где Pn(x)
– многочлен Тейлора:
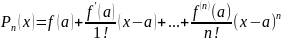 (3).
Если
функция f(x)
бесконечно дифференцируема в окрестности
точки а и остаточный член Rn(x)
стремится к нулю при n→∞,
то из формулы Тейлора получим разложение
функции f(x)
по степеням (х-а), называемое рядом
Тейлора:
(3).
Если
функция f(x)
бесконечно дифференцируема в окрестности
точки а и остаточный член Rn(x)
стремится к нулю при n→∞,
то из формулы Тейлора получим разложение
функции f(x)
по степеням (х-а), называемое рядом
Тейлора:
 (4).
Ряд Тейлора (4) можно составить для любой
бесконечно дифференцируемой функции
в окрестности точки а. такой ряд может
оказаться расходящимся или сходящимся,
но не к функции f(x).теорема1
Ряд Тейлора (4) функции f(x) сходится к
f(x) в точке х из некоторой окрестности
точки а тогда и только тогда, когда в
этой точке х остаточный член формулы
Тейлора (1) сходится к 0 при х→∞. отметим,
что проверка условия теоремы 1 во многих
случаях вызывает трудности, поэтому на
практике часто используют достаточное
условие разложимости функции в ряд
Тейлора, которое выражается следующей
теоремой. Теорема2.
Если
функция f(x) имеет производные любого
порядка на интервале (а-δ;а+δ) и все её
производные ограничены одной и той же
константой М на (а-δ;а+δ), то ряд Тейлора
(4) сходится к функции f(x)
на (а-δ;а+δ).
(4).
Ряд Тейлора (4) можно составить для любой
бесконечно дифференцируемой функции
в окрестности точки а. такой ряд может
оказаться расходящимся или сходящимся,
но не к функции f(x).теорема1
Ряд Тейлора (4) функции f(x) сходится к
f(x) в точке х из некоторой окрестности
точки а тогда и только тогда, когда в
этой точке х остаточный член формулы
Тейлора (1) сходится к 0 при х→∞. отметим,
что проверка условия теоремы 1 во многих
случаях вызывает трудности, поэтому на
практике часто используют достаточное
условие разложимости функции в ряд
Тейлора, которое выражается следующей
теоремой. Теорема2.
Если
функция f(x) имеет производные любого
порядка на интервале (а-δ;а+δ) и все её
производные ограничены одной и той же
константой М на (а-δ;а+δ), то ряд Тейлора
(4) сходится к функции f(x)
на (а-δ;а+δ).
29.
Представление элементарных ф-ций рядом
Маклорена. РядТейлора
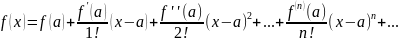 Если
а=0, то он наз-ся рядом Маклорена. При
разложении ф. f(x)
в ряд Макл.
Если
а=0, то он наз-ся рядом Маклорена. При
разложении ф. f(x)
в ряд Макл.
 (1)
поступаем так: вычисляем значения ф.
f(x)
и ее производных f’(x),
f”(x),…,
f(n)(x),…
. В точке х=0: записываем ряд (1) и находим
его интервалом сходимости, определяем
интервалом (-R;R),
в кот.остаточный член
(1)
поступаем так: вычисляем значения ф.
f(x)
и ее производных f’(x),
f”(x),…,
f(n)(x),…
. В точке х=0: записываем ряд (1) и находим
его интервалом сходимости, определяем
интервалом (-R;R),
в кот.остаточный член
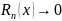 при
при
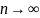 (если такой интервал сущ-ет, то на нем
справедливо разложение (1)).
(если такой интервал сущ-ет, то на нем
справедливо разложение (1)).
а)
пусть f(x)=ех,
f(n)(x)=
ех,
при х=0 f(n)(0)=1.
Ряд Маклорена будет иметь вид
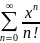 .
.
б)
пусть f(x)=sinx,
f(n)(x)=sin(x
+
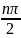 ),
, при х=0 f(0)=0,
f’(0)=1,
f”(0)=0,
f’’’(0)=-1,
f(4)(0)=0,
… Ряд Маклорена будет иметь вид
),
, при х=0 f(0)=0,
f’(0)=1,
f”(0)=0,
f’’’(0)=-1,
f(4)(0)=0,
… Ряд Маклорена будет иметь вид
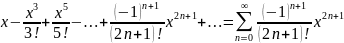 .
Тогда имеем
.
Тогда имеем
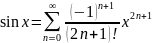 .
.
в)
аналогично
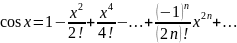 .
.
г)
разложим ф. f(x)=ln(1+x)
в ряд Макл.
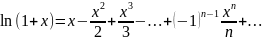 ,
,
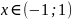 .
.
д)
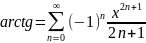 ,
.
При х=1 имеем
,
.
При х=1 имеем
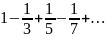 ;при х=-1
;при х=-1
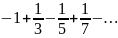 .
Эти ряды сходятся условно.
.
Эти ряды сходятся условно.
е)
разложение в ряд степенной ф. (1+х)α,(α≠0).
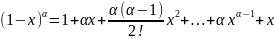 .
.
30.Понятие дифур-нияю Решение дифур-ний с разделяющимися переменными.Пусть x − независимая переменная, y= y(x) − искомая неизвестная функция. Дифференциальным уравнением называют уравнение, содержащие производную или производные неизвестной функции. Уравнения вида y' = f( x, y )называют дифференциальными уравнениями 1-го порядка, разрешенными относительно производной.Уравнения вида f(x,y,y’)=0 называют дифференциальными уравнениями 1-го порядка. Дифференциальные уравнения вида y ‘=g( y )*f (x) называют уравнениями с разделяющимися переменными. Решение уравнений с разделяющимися переменными осуществляется по следующей схеме: dy/dx=f (x)* g (y) ⇒dy/ g (y) =f(x)dx⇒ ∫dy /g(y)= ∫ f(x) dx .
31. Понятие диф. ур-ния. Решение однородныхдиф. ур-ний.При реш. различных задач матем., физ,. химии и др наук часто исп-сяур-ния,связывающие независимую переменную,искомую ф-цию и не производные. Такие ур-нияназ-с дифференциальными. Если искомая ф-ла зависит от 1 переменной,тодифф.ур. наз.обыкновенным. если искомая ф-ция зависит от неск.переменных,тодиф.ур. наз.ур-нием в частных производных. Наивысший порядок производной,входящий в диф.ур.,наз. порядком этого ур-ния.Диф.ур. P(x,y)dx+Q(x,y)dy=0 наз.однородным,если ф. P(x,y)и Q(x,y) (1)-однородные ф-ции одной степени. Разделив ур.(1) относит.произодн. dy\dx, запишем dy\dx=f(x,y) (2),где f(x,y)-однородная ф-ция нулевой степени. Покажем,что с пом.заменыy=ux,где u=u(x),однор. ур-ние сводится к ур-нию с разделяющимися переменными. Пусть t=1\х. подст. t в 1,получ. (1\tm)P(1;y\x)dx+ (1\tm)Q(1;y\x)dx=0. Учит.,чтоdy\dx=u+x(dy\dx), имеем P(1;u)+Q(1,u)+xQ(1,u)(du\dx)=0. Получ. (Q(1,u)du)\(P(1,u)+uQ(1,u)=-dx\x –ур-ние с раздел.переменными. При делении перем. могли быть утеряны решения вида u=a, где а-кореньур-нияP(1;u)+uQ(1,u)=0.
32.
Решение линейныхдифур-ний. Ур-ние вида
y’+p(x)y=q(x)
или dx/dy+p(y)x=q(y)
(p
и q
непрерывные на некотором интервале
I=(a,b)
ф-ции) наз линейным, первое относительно
y,
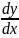 ,
а второе – относит x,
,
а второе – относит x,
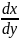 .
Если q(x)Ξ0
(Ξ
– равно тождественно)(q(y)Ξ0),
то ур-ниеназыв линейным однородным,
если q(x)≠0
(q(y)≠0)
– линейным неоднородным. Решение
линоднороднур-ния: y'+p(x)y=0(1).
Имеем
.
Если q(x)Ξ0
(Ξ
– равно тождественно)(q(y)Ξ0),
то ур-ниеназыв линейным однородным,
если q(x)≠0
(q(y)≠0)
– линейным неоднородным. Решение
линоднороднур-ния: y'+p(x)y=0(1).
Имеем
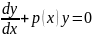 .
Разделив переменные, получим
.
Разделив переменные, получим
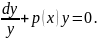 Проинтегрировав, будем иметь
Проинтегрировав, будем иметь
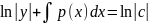 ,
тогда
,
тогда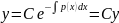 (2).
Т.к. y=0
также явл решением ур-ния (1), то фор-ла
(2) будет давать все решения ур-ния (1),
если считать параметр С произвольным.
Решение линнеоднур-ния: y'+p(x)y=q(x)(3).
Решение будем искать в виде y=C(x)y(4).
Подставляя (4)в (3), имеем
(2).
Т.к. y=0
также явл решением ур-ния (1), то фор-ла
(2) будет давать все решения ур-ния (1),
если считать параметр С произвольным.
Решение линнеоднур-ния: y'+p(x)y=q(x)(3).
Решение будем искать в виде y=C(x)y(4).
Подставляя (4)в (3), имеем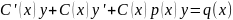 .
(C(x)[y'+p(x)y]=0).
Значит, C'(x)y=q(x),
следовательно
.
(C(x)[y'+p(x)y]=0).
Значит, C'(x)y=q(x),
следовательно
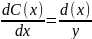 ,
отсюда следует,
,
отсюда следует,
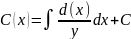 .
Подставляя най денноеC(x)
в (4), получим формулу Бернулли:
.
Подставляя най денноеC(x)
в (4), получим формулу Бернулли:
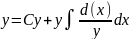 .
Описанный метод назыв методом вариации
произвольной постоянной или методом
Лагранжа.
.
Описанный метод назыв методом вариации
произвольной постоянной или методом
Лагранжа.
