Дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка — это уравнение, которое не содержит производных выше первого порядка от неизвестной функции. На Рисунке 1 показан пример того, как решить относительно простое дифференциальное уравнение:
с начальными условиями: y(0) = 4
Функция rkfixed на Рисунке 1 использует для поиска решения метод Рунге-Кутты четвертого порядка. В результате решения получается матрица, имеющая два следующих столбца:
Первый столбец содержит точки, в которых ищется решение дифференциального уравнения.
Второй столбец содержит значения найденного решения в соответствующих точках.
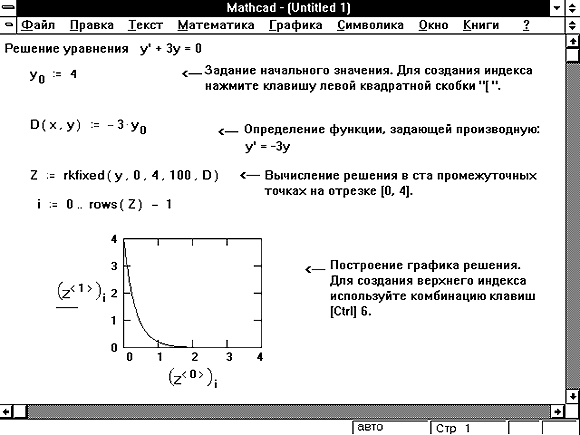
Рисунок 1: Решение дифференциального уравнения первого порядка.
Функция rkfixed имеет следующие аргументы:
rkfixed ( y, x1, x2, npoints, D)
y = |
Вектор начальных условий размерности n, где n — порядок дифференциального уравнения или число уравнений в системе (если решается система уравнений). Для дифференциального уравнения первого порядка, как, например, для уравнения, приведенного на Рисунке 1, вектор начальных значений вырождается в одну точку y0 = y(x1). |
x1, x2 = |
Граничные точки интервала, на котором ищется решение дифференциальных уравнений. Начальные условия, заданные в векторе y, — это значение решения в точке x1. |
npoints = |
Число точек (не считая начальной точки), в которых ищется приближенное решение. При помощи этого аргумента определяется число строк (1 + npoints) в матрице, возвращаемой функцией rkfixed. |
D (x, y) = |
Функция, возвращающая значение в виде вектора из n элементов, содержащих первые производные неизвестных функций. |
Наиболее трудная часть решения дифференциального уравнения состоит в определении функции D(x, y), которая содержит вектор первых производных от неизвестных функций. В примере, приведенном на Рисунке 1, было достаточно просто разрешить уравнение относительно первой производной , и определить функцию D(x, y). Иногда, особенно в случае нелинейных дифференциальных уравнений, это может быть трудно. В таких случаях иногда удаётся разрешить уравнение относительно в символьном виде и подставить это решение в определение для функции D(x, y). Используйте для этого команду Решить относительно переменной из меню Символика.
Рисунок 2: Более сложный пример, содержащий нелинейное дифференциальное уравнение.
Дифференциальные уравнения второго порядка
Как только Вы научились решать дифференциальное уравнение первого порядка, можно приступать к решению дифференциальных уравнений более высокого порядка. Мы начнем с дифференциального уравнения второго порядка. Основные отличия от уравнения первого порядка состоят в следующем:
Вектор начальных условий y теперь состоит из двух элементов: значений функции и её первой производной в начальной точке интервала x1.
Функция D(t, y) является теперь вектором с двумя элементами:
Матрица, полученная в результате решения, содержит теперь три столбца: первый столбец содержит значения t, в которых ищется решение; второй столбец содержит y(t); и третий — y'(t).
Пример, приведенный на Рисунке 3, показывает, как решить следующее дифференциальное уравнение второго порядка:
y'' = -y' + 2y y(0) = 1 y'(0) = 3
Рисунок 3: Решение дифференциального уравнения второго порядка.