Интегральное исчисление.
Функция нескольких переменных. Двойной интеграл. Определения. Свойства.
4.Двойной интеграл по области. Множество меры 0.
Есть
заданная и непрерывная на [a,b]
. Ее можно проинтегрировать:
А если функция двух или трех переменных?
Заданная и непрерывная в области D.
Тогда:
П
D
y
x
a
b
c
d
Если она ограничена, то всегда можно получить некоторый прямоугольник. Причем внутри D - , а в кусочках функцию можно определить как равную нулю.
Это произведение множеств
Это обозначение для прямоугольника
1.Двойной интеграл по прямоугольнику.
Определим интеграл для прямоугольника.
Раздробим его на кусочки.
По x – i
По y – j
i и j – номера кусочков
Выберем
точку
с
координатами
.
Посчитаем значение функции в этой точке.
И так, для каждого кусочка образовали интегральную сумму.
-
- площадь маленького прямоугольника
Если
существует предел от интегральной
суммы, когда ранг дробления по каждой
переменной
:
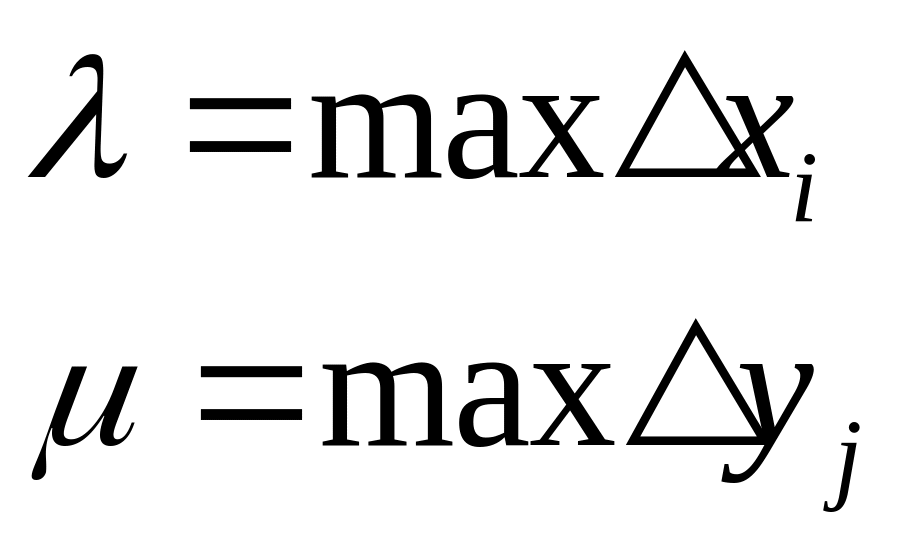
Если существует такой предел, не зависящий от выбора точек и от способа дробления то, он и будет интегралом:
3.Сумма Дарбу.
По аналогии можно определить верхние и нижние суммы Дарбу:
Пусть
Тогда
И
тогда наша сумма
расположена
между этими суммами Дарбу:
Для непрерывных или кусочно-непрерывных функций интеграл существует.
Если функция интегрируема, то сумма Дарбу сходится к интегралу:
Свойства интеграла.
1.Аддетивность
Если 
(эти множества не пересекаются)
Оно доказывается элементарно:
В
интегральном примере будут точки,
попадающие в
и
В
опрос
только в том, что в некоторые кусочки
могут попасть кусочки как
,
так и
Если функция интегрируема, то она должна быть ограничена. А если так , то эти кусочки, их общая площадь . И останется только интеграл по и интеграл по .
2. Линейность
а.
б.
Интеграл от суммы = сумме интегралов
3.
Если это справедливо, тогда справедливо следующее:
4. Если
-
интегрируемы, то произведение
тоже
интегрируемо
5.
Следует из свойства модуля, примененных к интегральным суммам.
Если функция интегрируема, то и ее модуль будет интегрируем.
6. Аналогично теорема о среднем.
Если
,
В
частном случае, когда
,
мы получаем:
2.Класс интегрируемых функций.
1.Непрерывные
функции
на
интегрируемы.
Доказательство:
По теореме Кантора функция равномерно непрерывна , если она замкнуто-ограничена
колебание функции
2. Всякая ограничено-непрерывная функция на D , за исключением конечного числа линий принадлежащих это области , интегрируема по этой области.
Д
оказательство:
с
Q
D
D-Q - замкнутая область
Q- открытая область
Разбиваем
область
Тогда,
=Q,
а остальные
лежат вне Q
Мера Жордана.
Есть некое множество – D.
Включим
в него некий прямоугольник
Характеристическую
функцию множества
определим
следующим образом:
{
И тогда под площадью множества M(D) понимается интеграл:
5.Сведение двойного интеграла к повторному.
Это способ реально посчитать интеграл.
Доказательство.
Опишем сначала для прямоугольника.
Пусть у нас функция интегрируема.
Введем обозначения:
Раздробим область.
Для всех точек имеем: (если x,y из соответствующего элементарного прямоугольника с номером i,j)
Теперь интегрируем это непрерывно по y в пределах маленького элементарного прямоугольника.
Просуммируем по всем прямоугольникам. Суммируем по вертикальной полосе (i).
i
Теперь
домножим на
и проинтегрируем по i от 1 до n:
Когда ранг дробления , то
А
интегрируем сумма
,
ну а это равно двойному интегралу:
Формула доказана.
Теперь если область не прямоугольник.
Предположим
сначала, что это криволинейная трапеция,
которая задается двумя функциями
.
В
D
a x
b
Включим эту трапецию в прямоугольник и применим формулу:
Основная формула для вычисления двойных интегралов.
С
лучай
сложной области.
Разбиваем эту сложную область на элементарные.
1
2
3
4
5
6
7
9
8
Если интегрируем сначала по х, то можно разбить так
Криволинейный интеграл первого рода.
З
адана
некая кривая (рассмотрим случай
плоскости).
В каждой точке кривой задана функция
.
Тогда можем ввести криволинейный интеграл первого рода.
Параметр S - параметр длины кривой (длина в текущей точке).
,
где
-
длина кривой. (не важно из какой точки
мы движемся: из А или из В)
В случае пространства:
Однако , обычно мы имеем параметрически заданную прямую:
Тогда интеграл выглядит:
Т.е. таким образом мы разбиваем кривую на кусочки.
Н
а
-том
кусочке
(длина
дуги
длине
участка ломаной)
Этот корень можно записать как:
В пределе это устремится к соответствующим производным.
Криволинейные интегралы второго рода.
Е
сть
кривая L в пространстве
выбрали на ней определенное направления.
Тогда можно определить такой криволиней
интеграл второго рода:
где
-
функции, заданые на нашей кривой. Будем
считать их непрерывными или
кусочно-непрерывными
-параметр
кривой:
(оно
пробегает такие значения)
Параметризация такова, что пробегается наша кривая.
Делай замену:
Тогда наш интеграл примет вид:
Интеграл не зависит от того, каким образом мы параметризовали кривую.
Есть
некоторая область в трехмерном
пространстве (частный случай – на
плоскоти). В каждой точке заданы три
функции
(или
-
на плоскости)
Мы можем считать, что в каждой точке задан некоторый вектор с координатами
Говорят, что задано векторное поле, когда в каждой точке области задан некоторый вектор.
П
усть
в нашей области задана некоторая кривая
Возникает вопрос, когда этот интеграл зависит от начальной и конечной точек, а когда от того по какой кривой мы интегрируем?
Если интеграл – функция от начальной
и конечной точек, то мы можем определить
потециал
Интеграл не зависит от пути интегрирования.
(знак «-» от того, что кривая пробегается в обратном направлении. И в параметризации:
Потенциал – это многомерный аналог неопределенного интеграла. Это некий аналог первообразной. Он определен с точностью до постоянного слогаемого.
Когда интеграл не зависит от пути интегрирования?
К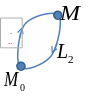
ритерий
потенциальности векторного поля.
(*) – это выполняется тогда, и только
тогда, когда:
или
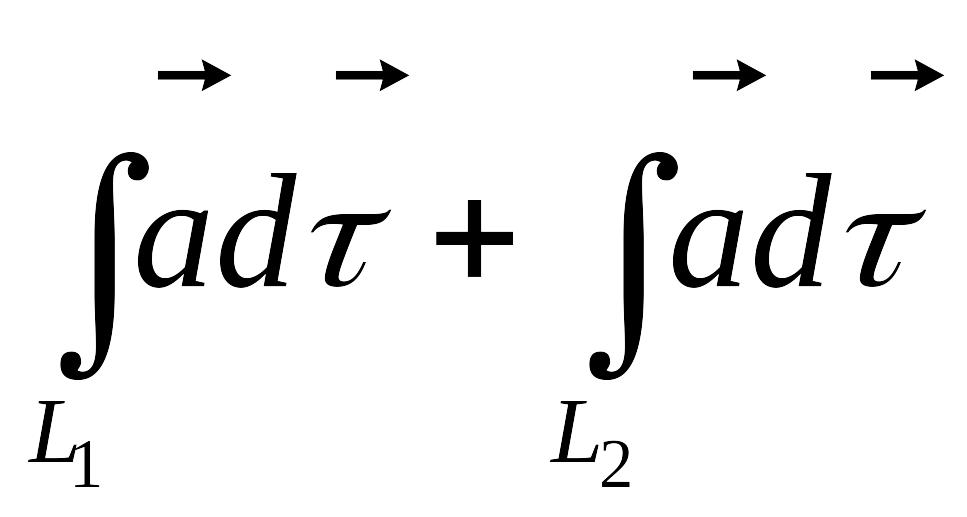= Знак «-» внизу интеграла
указывает на то, что интегрируем в
обратном направлении
-
контур. Мы движемся сначала по
,
а потом по
,
но в обратном направлении
=
Интеграл по кругу равен нулю. Для того, чтобы интеграл был независимым от пути интегрирования, надо чтобы интеграл по замкнутому контуру был равен 0.
Если выполняется равество (*), то интеграл по замкнутому кругу = 0.
Полу потенциально тогда, и только тогда, когда:
По
-
стрелки в обратную сторону.
Выразим через потенциал
- некоторые непрерывные функции.
Выполним приращение:
Если приращение достаточно маленькое, а область достаточно хорошая, то точка M1 достаточно близка к точке М и можно провести прямолинейный отрезок. Он тоже будет находиться в области точки М.
Тогда разница:
=
Но по этому пути
и
и
=
==
выбрали такую параметризацию когда
Воспользуемся теоремой о среднем:
==
В силу непрерывности функции
Зачит
(остальные случаи доказываются аналогично)
Предположим, что - непрерывно дифференцируемые функции. Тогда:
Тогда:
Это необходимое условие потенциальности.
Сначала докажем плоский случай ( нет
)
,
Для этого сначла выведем формулу Грина.
Формула Грина.
, где
-
так обозначается граница области D.
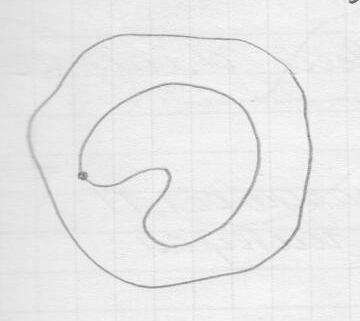
Если интеграл по внешнему контуру равен нулю, то равен нулю интеграл и по некоторому внутреннему контуру.
Формула Грина.
Сначало вывод для следующей области:
С
водим
двойной интеграл к повторному :
=
==
делаем замены чтобы обходить область всё время в положительном направлении.
Последние два интеграла равны нулю,
т.к.
не меняется.
==
- вдоль всей области
Если для
взять
такую область М, то так же получим
интеграл:
Эту область можно разбить на элементарные .
Провели вертикальную черту. Получили три кусочка.
По внутренним разрезам интегралы взаимно уничтожаются.
Если область с дырами, то дырка обходится в обратном направлении так, чтобы область находилась слева. Делается необходимые разрезы.
Что касается , то это делается следующим образом – область ограничивается горизонтальными линиями.
В
нутренние
интегралы также сокращаются.
В результате сложения получается формула Грина.
Необходимое и достаточное условие потенциальности поля.
Есть векторное поле.
Вектора с координатами
Необходимое и достаточное условие:
Обращение в ноль интеграла по любому замкнутому контуру С.
П
усть
область D
Односвязная и поле непрерывно дифференцируемое. Тогда можно применить формулу Грина.
Если везде в области
Значит везде в области интеграл = 0
Следовательно поле будет поленциально.
Теперь наоборот.
Псть в некоторой точке
область
Т.к. эти функции непрерывны, то в некоторой
области
они сохраняют знак
(разность
сохраняет знак)
Предлагаем, что вся лежит в области.
Тогда
Т.к.
(не только сохраняет знак, но и больше
некоторого
)
в точке
в
она может доходить до
Тогда
Т.е. это не ноль. Значит интеграл по границе не ноль, т.е. поле не будет потенциальным.
- необходимое и достаточное условие.
Замена переменных в двойном интеграле.
Дано:
Замена:
Выведем аналогичную формулу для двойного интеграла.
Замену будем считать взаимно однозначной.
В
ыбираем
область, а также функцию
выберем некоторую функцию
,
которая
Тогда - такая функция:
Тогда производная интеграла по верхнему
пределу будет
Следовательно:
Это частный случай формулы Грина, в котором P=0
В последнем одномерном интеграле можно сделать замену переменной.
=
Теперь сгруппируем:
=
[применим
формулу Грина, и предположим,
-
дважды дифференцируемые функции]
=
==
Найдем
и
подставим эти выражения в интеграл.
==
=
===
- якобиан. Это определитель матрицы.
это матрица дифференцированная от
замены переменных.
Разберемся теперь со знаком. Знак не должен зависить от того, какая у нас функция, а только от замены переменной.
Если функция положительная, а якобиан отрицательный, то знак «-», если якобиан положительный, то знак «+».
===
Знаки обхода соответсвтвия контуров меняются на противоположные, если якобиан отрицательным.
Формуле верна же для области, которую можно разбить на элементарные.