14. Метод вариации произвольных постоянных

Этот метод основан на том, что форма записи решения неоднородного уравнения такая же, что и у соответствующего однородного, с той лишь разницей, что произвольную постоянную С следует считать некоторой функцией переменной t, С = С(t), то есть  x(t)=C(t)e                                                   (3.5)

Функция C(t) должна быть такой, чтобы при подстановке (3.5) в уравнение (3.1) последнее обращалось в тождество. Подставляя x(t) и     C'(t)e =f(t)   или   C'{t)=f(t)e

Интегрируя, находим выражение для C(t):    (3.6)

Подставляя полученное выражение в (3.4), получаем общее решение линейного неоднородного уравнения (3.1) в виде  .                      (3.7)

Заметим, что первое слагаемое в формуле (3.7) является частным решением линейного неоднородного уравнения (3.1), в чем можно убедиться не­посредственной проверкой. Второе слагаемое является общим решением соответствующего однородного уравнения (3.3). Этот результат подтверждает известное свойство решений неоднородного уравнения.

Приведенные рассуждения позволяют сформулировать алгоритм решения уравнения (3.1).

15. Системы обыкновенных дифференциальных уравнений

Рассмотрим систему обыкновенных дифференциальных уравнений n–го порядка

 или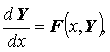 

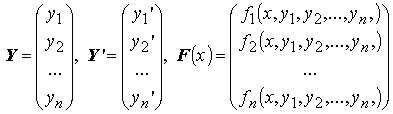
Задачей Коши для для этой системы называется следующая задача: найти такое решение Y = Y(x) системы Y' = F(x,Y), что Y(x₀)=Y₀, гдеY₀ — некоторый постоянный вектор.

 

Вектор-функция Y = Y(x,С), зависящая от произвольного вектора С, называется общим решением системы, если:

— при любом векторе C, вектор-функция Y(x,С) является решением системы;

— какова бы ни была начальная точка ((x₀, Y₀), существует такой вектор С⁽⁰⁾, что Y(x⁽⁰⁾,С⁽⁰⁾) = Y₀.

16. Числовые ряды. Основные теоремы о сходимости

Числовой ряд – это сумма членов числовой последовательности вида  .

Необходимый признак сходимости числового ряда:  Если ряд   сходится, то  . Данный признак означает, что если  , то ряд расходится. Например,   расходится, так как . Из выполнения условия   в общем случае не следует сходимость ряда  . Например, для ряда   (гармонический ряд), условие   выполнено, но данный ряд расходится.

17. Положительные числовые ряды. Признаки Коши и Даламбера

Положительные ряды

Если a_n ≥ 0 (n = 1, 2, 3, ... ), то ряд a₁ + a₂ + a₃ + ... называется положительным. В том случае, когда при всех n оказывается a_n > 0, будем называть ряд строго положительным.

     Положительные ряды обладают многими свойствами, сближающими их с обычными суммами конечного числа слагаемых.

     Легко видеть, что частичная сумма

S_n = a₁ + a₂ + ... + a_n

положительного ряда возрастает (может быть, не строго) с увеличением n. Так как всякая возрастающая числовая последовательность имеет конечный или бесконечный предел (причем члены последовательности не превосходят этого предела), то для любого положительного ряда существует предел

     Этот предел будет конечным или бесконечным, смотря по тому, ограничено сверху или нет множество частичных сумм {S_n}

Теорема (признак Даламбера). Пусть для числового ряда с положительными членами:

cуществует  l, то

при l<1 ряд сходится,

при l>1 ряд расходится,

при l=1 ряд может сходиться или расходиться (в этом случае признак на вопрос о сходимости ряда ответа не дает).

По определнию предела    > 0   N=N( ), что   n>N выполняется неравенство:

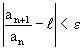 или  .

Выберем N так, чтобы для n>N было l+  =q<1, тогда

Ряд a_Nq+a_Nq²+...+a_Nq^m+... сходится, так как знаменатель прогрессии q<1. Тогда по теореме 1 ряд   также сходится.

Для случая q>1 доказательство аналогично, только нужно рассмотреть  .

Признак Коши: Если существует  , то при l<1 ряд сходится; l>1 - ряд расходится; l=1 — определить сходимость невозможно.

Доказательство признака Коши аналогично доказательству признака Даламбера.