36 Задвча обработки наблюдений

Прямая задача обработки наблюдений

Дана несовместная система линейных уравнений y=Ax (y - n-мерный вектор наблюдаемых значений, A - известная матрица размерности n x n, x - неизвестный m-мерный вектор оцениваемых параметров). Решение задачи по методу наименьших квадратов дается m - мерным вектором x _r = (A^TA) ^{- 1} A^Ty , где T - обозначает транспонирование.

2. Обратная задача обработки наблюдений

По известному решению x _r вычисляем идеальную реализацию в виде n - мерного вектора y _r = A x _r . Определяем n - мерный вектор ошибок Δ = y - y _r . Находим максимальную ошибку e = max (|Δ|₁ , ..., |

Δ|_n). Строим множество реализаций в виде интервального вектора [y] = [y₁ , y₂], где y₁ = y - εI , y₂ = y + εI , I = (1,...,1) ^T - единичный n-мерный вектор.

Метод наименьших квадратов (МНК, OLS, Ordinary Least Squares) — один из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Метод основан на минимизации суммы квадратов остатков регрессии.

Необходимо отметить, что собственно методом наименьших квадратов можно назвать метод решения задачи в любой области, если решение заключается или удовлетворяет некоторому критерию минимизации суммы квадратов некоторых функций от искомых переменных. Поэтому метод наименьших квадратов может применяться также для приближённого представления (аппроксимации) заданной функции другими (более простыми) функциями, при нахождении совокупности величин, удовлетворяющих уравнениям или ограничениям, количество которых превышает количество этих величин и т.д.

37 Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида

F(x, y, y' )=0,     

где F — известная функция трех переменных, определенная в области G из R³,   x — независимая переменная из интервала (a, b), y(x) — неизвестная функция, y'(x) — ее производная.  

Обыкновенные дифференциальные уравнения, разрешенные относительно производной, т.е. уравнения вида 

y'=f(x, y)

называют уравнениями в нормальной форме.

  Общим решением дифференциального уравнения называется такое его решение, содержащее произвольные постоянные, из которого любое частное решение может быть получено при соответствующем подборе произвольных постоянных.

   Частное решение дифференциального уравнения — это решение, не содержащее произвольных постоянных.

Начальное условие

        при математическом анализе процесса, состояние этого процесса в какой-либо момент времени, принятый за начальный. Если процесс описывается дифференциальным уравнением, то задача об отыскании решений по Н. у. называется Коши задачей (См. Коши задача). Для уравнения

         

         Н. у. состоит в задании

         

        при значении t = t₀ Если n = 2 и y = y (t) — закон движения материальной точки, то в Н. у. задаётся положение точки и её скорость в момент t = t₀. Н. у. для дифференциального уравнения с частными производными ставится аналогично. Так, для уравнения свободных колебании струны

         

Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла)дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).

Задача Коши обычно возникает при анализе процессов, определяемых дифференциальным законом эволюции и начальным состоянием (математическим выражением которых и являются уравнение и начальное условие). Этим мотивируется терминология и выбор обозначений: начальные данные задаются при  , а решение отыскивается при  . а 

(а - данная функция) и при х=х ₀ принимает значение и ₀:

Для линейных дифференциальных уравнений с частными производными 

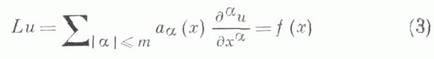
 Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)

            Если функция f(x, y) непрерывна в некоторой области  D в плоскости XOY и имеет в этой области непрерывную частную производную  , то какова бы не была точка (х₀, у₀) в области D, существует единственное решение   уравнения  , определенное в некотором интервале, содержащем точку х₀, принимающее при х = х₀ значение (х₀) = у₀, т.е. существует единственное решение дифференциального уравнения.

38 дифференциальное уравнение с разделяющ переменными.Дифференциальные уравнения   называют уравнениями с разделенными переменными. Название этого вида дифференциальных уравнений достаточно показательно: выражения, содержащие переменные x и y, разделены знаком равенства, то есть, находятся по разные стороны от него. Будем считать, что функции f(y) и g(x) непрерывны. Общим интегралом уравнения с разделенными переменными является равенство  . Если интегралы из этого равенства выражаются в элементарных функциях, то мы можем получить общее решение дифференциального уравнения как неявно заданную функцию Ф(x, y) = 0, а иногда получается выразить функцию y в явном виде.

Обыкновенное уравнение первого порядка   называется однородным относительно x и y, если функция   является однородной степени 0:

.

Однородную функцию можно представить как функцию от  :

.

Используем подстановку  , а затем воспользуемся правилом произведения :  . Тогда, дифференциальное уравнение  сводится к уравнению с разделяющимися переменными:

Определение линейного уравнения первого порядка

Дифференциальное уравнение вида

где a(x) и b(x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка.

39 Дифференциальные уравнения, допускающие понижение порядка

В общем случае дифференциальное уравнение второго порядка можно записать в виде где F − заданная функция указанных аргументов.  Если дифференциальное уравнение можно разрешить относительно второй производной y'', то его можно представить в следующем явном виде: В частных случаях функция f в правой части может содержать лишь одну или две переменных. Такиенеполные уравнения включают в себя 5 различных типов: С помощью определенных подстановок эти уравнения можно преобразовать в уравнения первого порядка.  В случае произвольных дифференциальных уравнений второго порядка, их порядок можно понизить, если эти уравнения обладают определенной симметрией. Ниже мы обсудим 2 типа таких уравнений (случаи 6 и 7): -Функция F(x, y, y', y'') является однородной функцией аргументов y, y', y''; -Функция F(x, y, y', y'') является точной производной функции первого порядка Ф(x, y, y'). 40. Линейное однородное дифференциальное уравнение второго порядка имеет вид   Свойства решений линейного однородного дифференциального уравнения (25). .1. Теорема о линейности пространства частных решений линейного однородного дифференциального уравнения. Множество частных решений линейного однородного дифференциального уравнения образует линейное пространство.  Док-во. Требуется доказать, что множество частных решений линейного однородного дифференциального уравнения (25) (или, что тоже самое, (21)), т.е. не менее n раз дифференцируемых функций y(x) для которых Ln(y) = 0, является линейным пространством. Для этого достаточно доказать, что если функции y, y1(x), y2(x) - частные решения (25), то функции Cy, y1(x) + y2(x) - тоже частные решения (25). Действительно, пользуясь свойствами пункта .2. Линейный дифференциальный оператор и его свойства, получим  если Ln(y) = 0, то Ln(Cy) = CLn(y) = 0;  если Ln(y1) = 0 и Ln(y2) = 0, то Ln(y1 + y2) = Ln(y1) + Ln(y2) = 0.  Следствие. Если y1(x), y2(x), …, yn(x) - частные решения уравнения (25), то их линейная комбинация C1 y1(x) + C2 y2(x) + …+ Cn yn(x) - тоже частное решение этого уравнения. 41.  Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами Рассмотрим линейное дифференциальное уравнение вида где p, q − постоянные коэффициенты.  Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение: Обшее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которое в данном случае будет являться квадратным уравнением. Возможны следующие случаи:Дискриминант характеристического квадратного уравнения положителен: D > 0. Тогда корни характеристического уравнения k1 и k2 действительны и различны. В этом случае общее решение описывается функцией где C1 и C2 − произвольные действительные числа. Дискриминант характеристического квадратного уравнения равен нулю: D = 0. Тогда корни действительны и равны. В этом случае говорят, что существует один корень k1 второго порядка. Общее решение однородного дифференциального уравнения имеет вид: Дискриминант характеристического квадратного уравнения отрицателен: D < 0. Такое уравнение имеет комплексно-сопряженные корни k1 = α + βi, k1 = α − βi. Общее решение записывается в виде

 

42.Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Структура общего решения Линейное неоднородное уравнение данного типа имеет вид: где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение: Теорема: Общее решение неоднородного уравнения является суммой общего решения y0(x) соответствуюшего однородного уравнения и частного решения y1(x) неоднородного уравнения: . Метод вариации постоянных Если общее решение y0 ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных.  Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид: Вместо постоянных C1 и C2 будем рассматривать вспомогательные функции C1(x) и C2(x). Будем искать эти функции такими, чтобы решение удовлетворяло неоднородному уравнению с правой частью f(x).  Неизвестные функции C1(x) и C2(x) определяются из системы двух уравнений: Метод неопределенных коэффициентов Правая часть f(x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов.  Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как   где Pn(x) и Qm(x) − многочлены степени n и m, соответственно. В обоих случаях выбор частного решения должен соответствовать структуре правой части неоднородного дифференциального уравнения.