П ервообра́зной [1] или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.Так, например, функция   является первообразной  семейство первообразных функции x2 можно обозначить как F(x) = x3 / 3 + C, где C — любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения C.Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная нтегрируемой функции f, то:Это соотношение называется формулой Ньютона — Лейбница.Благодаря этой связи множество первообразных данной функции f называют неопределённым интегралом (общим интегралом)

Теорема. Если F1 (x) и F2 (х)- две первообразные от функции f(x) на отрезке [a,b], то разность между ними равна постоянному числу.

Доказательство. В силу определения первообразной имеем F1 ′(х)= f(x), F2 ′(х)= f(x) (1)При любом значении х на отрезке [a,b].Обозначим F1 (х)- F2 (х) =φ(х) (2)

Тогда на основании равенств (1) будет F′1 (х)- F′2 (х)= f(x)- f(x)=0 или φ′(х)=[ F′1 (х)- F′2 (х)]′≡0 при любом значении х на отрезке [a,b]. Но из равенства φ′(х)=0 следует, что φ(х) есть постоянная. Действительно, применим теорему Лагранжа к функции φ(х), которая, очевидно, непрерывна и дифференцируема на отрезке [a,b]. Какова бы ни была точка х на отрезке [a,b], мы имеем в силу теоремы Лагранжа φ(х)- φ(а)= (х-а) φ′(z), где а < z < x.Так как φ′(z)=0, то φ(х)- φ(а)=0, или φ(х)= φ(а). (3)

Таким образом, функция φ(х) в любой точке х отрезка [a,b] сохраняет значение φ(а), а это значит, что функция φ(х) является постоянной на отрезке [a,b]. Обозначая постоянную φ(а) через С, из равенств (2) и (3) получаем F1 (х)- F2 (х) = С.

Из доказанной теоремы следует, что если для данной функции f(x) найдена какая- нибудь одна первообразная F(x), то любая другая первообразная для f(x) имеет вид F(x)+ С, где С = const/

Неопределённый интегра́л для функции   - это совокупность всех первообразных данной функции.

Св1. Постоянный множитель можно вынести за знак интеграла:

Св2. Интеграл алгебраической суммы равен алгебраической сумме интегралов: Первые два свойства выражают линейность интеграла.

Св 4.3. Вид интеграла не зависит от вида переменной интегрирования: (4.12)или, что тоже самое, (4.12')где   — непрерывная вместе со своей производной функция.

Св4. Имеет место следующее равенство: (4.42)

где u и v — две непрерывно дифференцируемые функции

Св 4.1. Постоянный множитель можно вынести за знак интеграла: (4.4)Продифференцируем левую и правую части равенства, получим:  и  (4.5)

В левой части по формуле (2.8) получаем: (4.6)в правой части по правилам дифференцирования получаем: (4.7)

Воспользовавшись снова (2.8) окончательно получаем: (4.8Равенство правой и левой частей доказывает рассматриваемое свойство.

Интегрирование по частям. Пусть - дифференцируемые функции, тогда справедлива формула: , или короче: . Эта формула используется в тех случаях, когда подынтегральное выражение можно так представить в виде , что интеграл вычисляется проще исходного.

Пример: Вычислить .

Положим . Тогда . В качестве выберем первообразную при . Получим . Снова . Тогда . Окончательно получим: . Замечание 26.5: Иногда при вычислении интеграла методом интегрирования по частям получается зависимость: . Откуда можно получить выражение для первообразной: .

1. Задача о массе стержня II. Задача о пройденном пути III. Задача о площади криволинейной трапеции

Пусть на замкнутом промежутке [a, b] задана функция f(x). Проделаем следующие операции:

Раздробим [a, b] на части точками x0 = a < x1 < x2 < ... < xn-1 < xn = b, причем наибольшую из разностей xk+1 - xk обозначим через λ. 2) В каждом частичном промежутке [xk, xk+1] выберем по точке ξk и вычислим f(ξk). 3) Умножим f(ξk) на длину (xk+1 - xk) соответствующего промежутка [xk, xk+1]. 

Сложим все найденные произведения. Сумму будем называть интегральной суммой.5) Будем изменять произведённое дробление [a, b] так, чтобы величина λ стремилась к нулю. Если при этом существует конечный предел (4)не зависящий от выбора точек ξk, то этот предел называется определенным интегралом от функции f(x) по промежутку [a, b] и обозначается через

Т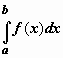 еорема существования определённого интеграла. Если функция f(x) непрерывна на отрезке [a,b], то она интегрируема по этому отрезку. Примем это утверждение без доказательства, поясним только его смысл. Интегрируемость функции означает существование конечного предела последовательности интегральных сумм, т.е. такого числа 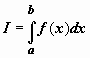 , что для любого   найдётся такое число  , что как только разбиение отрезка удовлетворяет неравенству  , то, независимо от выбора точек  выполняется неравенство. Требование непрерывности f(x) достаточно для интегрируемости, но не является необходимым. Интегрируемы функции, имеющие конечное или даже счётное число точек разрыва на [a,b] при условии их ограниченности (т.е. все точки разрыва должны быть точками разрыва первого рода). Неограниченная функция не может быть интегрируемой (идея доказательства этого утверждения: если f(x) неограничена на [a,b], то она неограничена на каком-либо [xi-1 , xi], т.е. на этом отрезке можно найти такую точку  , что слагаемое  , а следовательно, и вся интегральная сумма, будет больше любого наперед заданного числа). 

. Геометрический смысл определённого интеграла. Как следует из пункта 11.1.1, если f(x) >0 на отрезке [a,b], то  равен площади криволинейной трапеции ABCD, ограниченной снизу отрезком [a,b], слева и справа - прямыми x = a и x = b, сверху – функцией y = f(x).

5. Теоремы об оценке интеграла.

5.1. Если на отрезке функция удовлетворяет неравенству , то .

Док-во. Докажем левое неравенство (цифрами над знаками импликации обозначены номера применяемых ранее доказанных свойств): . Аналогично доказывается и правое неравенство.

5.2. Если функция интегрируема по отрезку , то .

Док-во. .

8. Теорема о среднем. Если непрерывна на отрезке , то существует точка , такая что 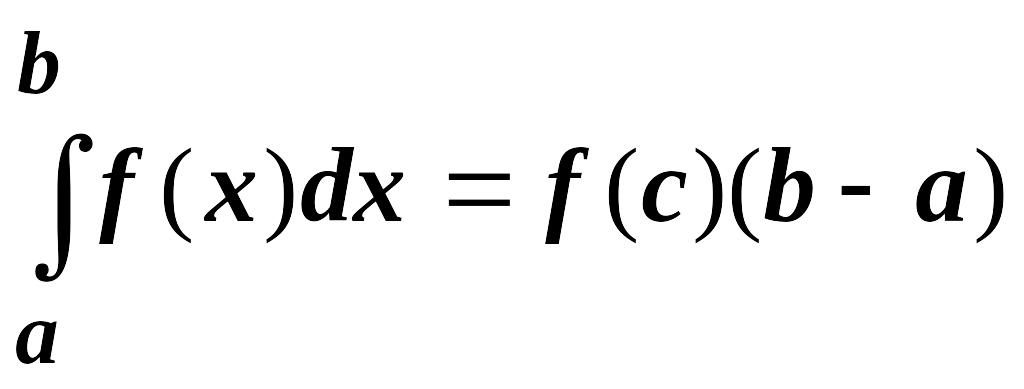. Док-во. Функция, непрерывная на отрезке, принимает на этом отрезке своё наименьшее и наибольшее значения. Тогда . Число заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между и . Таким образом, существует точка , такая что .

Это свойство имеет простую геометрическую интерпретацию: если непрерывна на отрезке , то существует точка такая, что площадь криволинейной трапеции равна площади прямоугольника с основанием и высотой (на рисунке выделен цветом).

Формула Ньютона-Лейбница. Если непрерывна на отрезке , и - некоторая первообразная функции , то . Док-во. Мы установили, что функция - первообразная непрерывной . Так как - тоже первообразная, то . Положим в этом равенстве . Так как , то . В равенстве переобозначим переменные: для переменной интегрирования вернёмся к обозначению , верхний предел обозначим . Окончательно, .Разность в правой части формулы Нь-Ле обозначается специальным символом: (здесь читается как "подстановка от до "), формулу Ньа-Лей обычно записывают так: . Пример применения формулы НЛей: .

Ф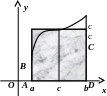 ормула интегрирования по частям для определённого интеграла. Если - непрерывно дифференцируемые функции, то . Док-во. Интегрируем равенство в пределах от до : . Функция в левом интеграле имеет первообразную , по формуле Ньютона-Лейбница 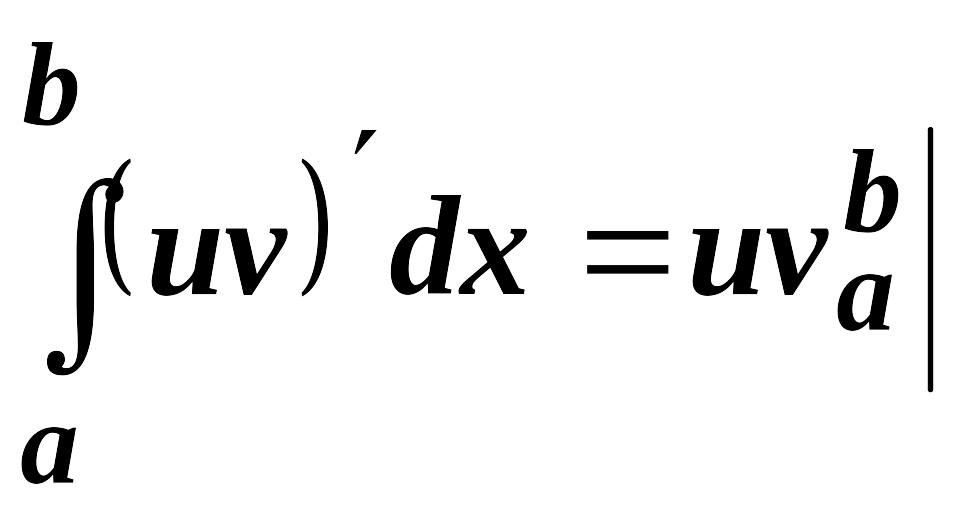, следовательно, , откуда и следует доказываемое равенство.: .

Замена переменной в определённом интеграле. Теорема. Пусть функция определена, непрерывно дифференцируема и монотонна на отрезке , ,функция непрерывна на отрезке .

Тогда .Док-во. Пусть - первообразная для функции , т.е. , тогда - первообразная для функции . , что и требовалось доказать.

При решении задач нельзя забывать о том, что при переходе к новой переменной надо обязательно вычислить новые пределы интеграла.

интегралы, для которых нарушаются эти требования (т.е. неограничена либо подынтегральная функция, либо область интегрирования, либо и то, и другое вместе) несобственными.

Определение несобственного интеграла по бесконечному промежутку. Пусть функция f(x) определена на полуоси и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла 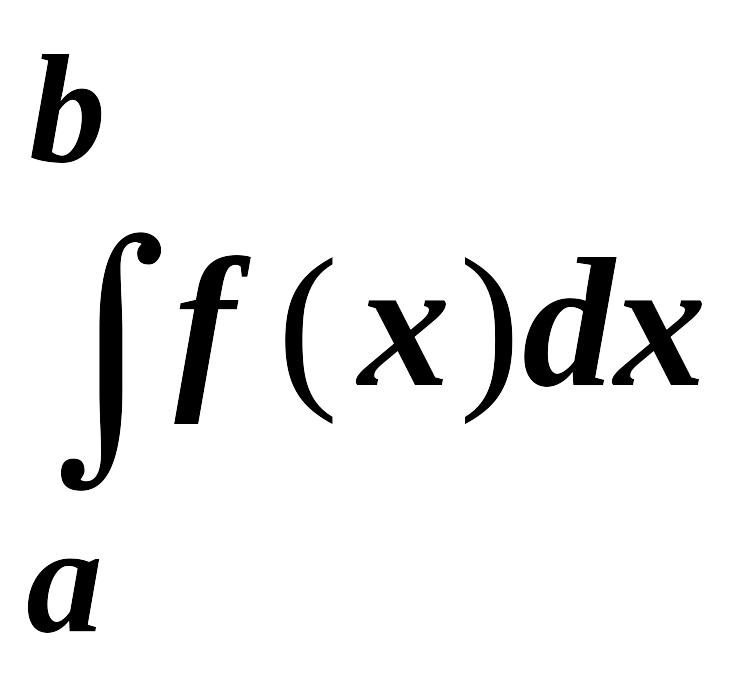при называется несобственным интегралом функции f(x) от a до и обозначается .

Итак, по определению, . Если этот предел существует и конечен, интеграл называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся.

пр сход Абеля: пусть функции f(x) и g(x) определены в промежутке , причём 1. f(x) интегрируема в этом промежутке, т.е. интеграл сходится (условно или абсолютно);