Билет №1

Логические функции. Таблица истинности.

В русском языке сложные предложения получаются путем соединения простых предложений с помощью союзов а, но, если .. то, тогда и только тогда, когда, или, и, аналогично в алгебре логики простые высказывания соединяются в сложные с помощью так называемых логических связок.

Если простое высказывание является истинным, то оно принимает значение логической переменной 1, иначе 0.

Основными операциями являются:

• Отрицание (не)

• Дизъюнкция (логическое сложение, v)

• Конъюнкция (логическое умножение,^)

• Импликация ( → )

• Эквиваленция (↔)

Отрицанием или инверсией высказывания А называется высказывание , которое истинно, когда высказывание А ложно, и наоборот.

Дизъюнкцией высказываний А и В называется высказывание АvВ, которое истинно тогда и только тогда, когда истинно хотя бы одно из высказываний.

Конъюнкцией высказывания А и В называется высказывание А^В, которое истинно тогда и только тогда, когда истины оба высказывания.

Импликацией высказываний А и В является высказывание А→В, которое ложно тогда и только тогда, когда из истины следует ложь.

Эквиваленцией высказывания А и В называется высказывание А↔В, которое истинно тогда и только тогда, когда либо истинно либо ложно одновременно оба высказывания.

Соответствия в АЛ	Название операции	Талица истинности
	отрицание	А 0 1 1 0
АvВ	дизъюнкция	А В АvВ 0 0 0 0 1 1 1 0 1 1 1 1
А^В	конъюнкция	А В А^В 0 0 0 0 1 0 1 0 0 1 1 1
А→В	Импликация	А В А→В 0 0 1 0 1 1 1 0 0 1 1 1
А↔В	эквиваленция	А В А↔В 0 0 1 0 1 0 1 0 0 1 1 1

Билет №2

Дизъюнктивная и коньюктивная нормальные формы.

Литерой  называется элемент высказывания x или её отрицание.

Элементарной дизъюнкцией называется выражение следующего вида:

,

где  литера.

Элементарной конъюнкцией называется выражение следующего вида:

,

Дизъюнктивной нормальной формой (ДНФ) формулы называется выражение вида:

,

где  элементарная конъюнкция.

Конъюнктивной нормальной формой (КНФ) формулы называется выражение вида:

,

где  элементарная дизъюнкция.

Любую формулу можно представить в виде ДНФ или КНФ.

Совершенной дизъюнктивной нормальной формой (СДНФ) формулы называется такая ДНФ, для которой выполняются следующие условия:

1. Все элементарные конъюнкции, входящие в ДНФ , различны.

2. Все элементарные конъюнкции, входящие в ДНФ , содержат литеры, соответствующие всем переменным.

3. Каждая элементарная конъюнкция, входящая в ДНФ , не содержит двух одинаковых литер.

4. Каждая элементарная конъюнкция, входящая в ДНФ , не содержит переменную и ее отрицание.

Совершенной конъюнктивной нормальной формой (СКНФ) формулы называется такая КНФ, для которой выполняются следующие условия:

1. Все элементарные дизъюнкции, входящие в КНФ , различны.

2. Все элементарные дизъюнкции, входящие в КНФ , содержат литеры, соответствующие всем переменным.

3. Каждая элементарная дизъюнкция, входящая в КНФ , не содержит двух одинаковых литер.

4. Каждая элементарная дизъюнкция, входящая в КНФ , не содержит переменную и ее отрицание.

Билет №3

Законы логики, равносильные преобразования.

Формулой математической логики называется сложное высказывание, которое получено из элементарных высказываний с использованием логических операций.

Две формулы равносильны, если они принимают одинаковые логические значения на любом наборе значений входящих в формулу элементарных высказываний. Равносильность формул обозначается  A  B.

Формулы равносильности:

1. Коммутативность

АVВ  ВVА

2. Ассоциативность

АV(ВVС)  (АVВ)VС

3. Дистрибутивность

АV(В^С)  (АVВ)^(АVС)

4. Идемпотентность

АVА  А

5. Поглощение

АV(АVВ)  А A^(AVB)≡A

6. Закон де Моргана

 ^  V

7. АV1  1 А^1  A

8. Закон противоречия

AV  A A^  

9. Закон двойного отрицания

 A

10. Отрицание  1 ,  0

11. AB  VB

12. AB  (AB)^(BA)

13. Закон контрапозиции AB  →

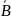
14. Закон склеивания

15. Закон тождества А≡А

16. Закон противоречия А^ ≡0

Билет №4

Функции АЛ. Представление булевых функций в виде формул логики определенного вида.

Пусть - произвольная функция алгебры логики переменных.

Рассмотрим формулу

(1)

которая составлена следующим образом: каждое слагаемое этой логической суммы представляет собой конъюнкцию, в которой первый член является значением функции при некоторых определенных значениях переменных , остальные же члены конъюнкции представляют собой переменные или их отрицания. При этом под знаком отрицания находятся те и только те переменные, которые в первом члене конъюнкции имеют значение 0..

Вместе с тем формула (1) содержит в виде логических слагаемых всевозможные конъюнкции указанного вида.

Ясно, что формула (1)полностью определяет функцию . Иначе говоря, значения функции и формулы (1) совпадают на всех наборах значений переменных . То есть функция

Составление формул по таблице истинности. может быть представлена в виде:

Билет №5

Разложение булевой функции по одной или нескольким переменным. Совершенная дизъюнктивная нормальная форма.

Совершенной дизъюнктивной нормальной формой (СДНФ) формулы называется такая ДНФ, для которой выполняются следующие условия:

1. Все элементарные конъюнкции, входящие в ДНФ , различны.

2. Все элементарные конъюнкции, входящие в ДНФ , содержат литеры, соответствующие всем переменным.

3. Каждая элементарная конъюнкция, входящая в ДНФ , не содержит двух одинаковых литер.

4. Каждая элементарная конъюнкция, входящая в ДНФ , не содержит переменную и ее отрицание.

СДНФ можно получить двумя способами:

1. по таблице истинности;

2. с помощью равносильных преобразований.

Первый способ получения СДНФ рассмотрен выше. Рассмотрим второй способ, который состоит в следующем:

С помощью равносильных преобразований формулы получают ДНФ . При этом в полученной ДНФ возможны следующие ситуации:

1. Элементарная конъюнкция ДНФ не содержит переменную , тогда используются следующие равносильные преобразования:

2. Если в ДНФ входят две одинаковые элементарные конъюнкции, то используя следующее равносильное преобразование:

,

одну элементарную конъюнкцию можно отбросить.

3. Если элементарная конъюнкция ДНФ содержит одновременно переменную и ее отрицание, то используя следующие равносильные преобразования:

,

эту элементарную конъюнкцию можно отбросить

4. Если элементарная конъюнкция ДНФ содержит дважды переменную , то используя следующее равносильное преобразование:

,

одну переменную можно отбросить

СДНФ формулы существует в единственном виде.

Билет №6

Разложение булевой функции по одной и нескольким переменным. Совершенная конъюктивная нормальная форма.

Совершенной конъюнктивной нормальной формой (СКНФ) формулы называется такая КНФ, для которой выполняются следующие условия:

1. Все элементарные дизъюнкции, входящие в КНФ , различны.

2. Все элементарные дизъюнкции, входящие в КНФ , содержат литеры, соответствующие всем переменным.

3. Каждая элементарная дизъюнкция, входящая в КНФ , не содержит двух одинаковых литер.

4. Каждая элементарная дизъюнкция, входящая в КНФ , не содержит переменную и ее отрицание.

СКНФ можно получить двумя способами:

1. по таблице истинности;

2. с помощью равносильных преобразований.

По первому способу по таблице истинности получаем СДНФ , а СКНФ можно получить, следуя следующему правилу

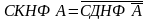
С помощью равносильных преобразований формулы получают КНФ . При этом в полученной КНФ возможны следующие ситуации:

1. Элементарная дизъюнкция КНФ не содержит переменную , тогда используются следующие равносильные преобразования:

2. Если в КНФ входят две одинаковые элементарные дизъюнкции, то используя следующее равносильное преобразование:

,

одну элементарную дизъюнкцию можно отбросить.

3. Если элементарная дизъюнкция КНФ содержит одновременно переменную и ее отрицание, то используя следующие равносильные преобразования:

,

эту элементарную дизъюнкцию можно отбросить.

4. Если элементарная дизъюнкция КНФ содержит дважды переменную , то используя следующее равносильное преобразование:

,

одну переменную можно отбросить.

СКНФ формулы существует в единственном виде.

ПРИМЕР

Получить СКНФ формулы

С помощью равносильных преобразований получаем СКНФ :

С помощью таблицы истинности получаем СДНФ :

0	0	0	1	0	1	0
0	0	1	0	0	1	0
0	1	0	1	1	1	0
0	1	1	0	0	1	0
1	0	0	1	0	0	1
1	0	1	0	0	0	1
1	1	0	1	1	1	0
1	1	1	0	0	0	1

СДНФ

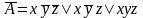
Очевидно, что в результат двух способов совпадает.

СДНФ формулы можно получить из СКНФ , используя следующее правило:

_{Билет №7}

_{Теорема Поста}

Функциональный набор логических функций  это такой набор функций, который позволяет любую функцию математической логики описать с помощью функций данного набора.

Теорема Поста. Для того чтобы набор функций {f₁,f₂,……f_n} был функционально полный необходимо и достаточно, чтобы для всего набора функций в целом не выполнялись свойства сохранения нуля, сохранения единицы, линейности, монотонности и самодвойственности.

Полноту набора удобно определять по таблице Поста, в клетках которой ставится знак «+» или «-» в зависимости от того, обладает функция из этого набора тем или иным свойством. В силу теоремы Поста для полноты системы необходимо и достаточно, чтобы в каждом столбце был хотя бы один минус.

{ }	T0	T1	L	M	S
F1	+	+	+	+	
F2					+

ПРИМЕР

Доказать, что набор функций6 дизъюнкция и отрицание является функционально полным.

	T0	T1	L	M	S
			+		+
V	+	+		+	

Теорема Поста о полноте

Для того чтобы система функций была полной, необходимо и достаточно, чтобы она не содержалась целиком ни в одном из классов T0, T1, L, S, M.

Доказательство. Докажем необходимость этого условия. Пусть система

N = {f1, f2, ...fs, ...} полна в Р2, покажем, что тогда она не лежит целиком в Q, где через Q обозначим любой из классов T0, T1, L, S, M. Докажем от противного, пусть N ??Q, очевидно, [N] ??[Q] = Q, но [N] = P2, т.к. N – полна в Р2, отсюда Р2=Q, но это не так. Необходимость доказана.

Докажем достаточность. Пусть F = {f0, f1, fL, fm, fs}, где f0?T0, f1?T1, fL?L, fs?S и fm?M. Покажем, что суперпозицией функций системы F можно получить полную систему G = {x1&x2, }.

1. Пусть g(x) = f0(x, …, x). Тогда g(0) = f( 0, …, 0) = 1. Далее возможны два случая:

g(1) = 1. Тогда g(x) ? 1. Функция h(x) = f1(g(x), …, g(x)) = f1(1, …, 1) = 0, т.е. h(x) ? 0. Получили константы 0 и 1;

g(1) = 0. Тогда g(x) = . По лемме о несамодвойственной функции суперпозицией над {fs, } можно получить одну из констант, например, 0. Тогда f0(0, …, 0) = 1 есть другая константа.

В обоих случаях получили обе константы.

2. По лемме о немонотонной функции суперпозицией над {fm, 0, 1} можно получить отрицание.

3. По лемме о нелинейной функции суперпозицией над {fL, 1, } можно получить конъюнкцию. Теорема доказана.

Следствие. Всякий замкнутый класс функций из Р2, не совпадающий с Р2 содержится, по крайней мере, в одном из замкнутых классов T0, T1, L, S, M. Действительно, если N не является подмножеством Q, то [N] = P2, что неверно.

Билет №8

Множества. Функции. Суперпозиция функций.

Множеством S называется объединение в одно целое объектов, хорошо различимых нашей мыслью или интуицией. Эти объекты называется элементами множества S. Такое интуитивное определение дал немецкий математик Г. Кантор. В данном определении важны следующие два момента:

1. Множество- это нечто, состоящее из хорошо различимых объектов.

2. Это нечто мыслится как единое целое.

Множества бывают конечными и бесконечными, Количество элементов в конечном множестве называется мощностью множества. Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается . Множество, включающее в себя в се рассматриваемые множества, называется универсальным множеством или универсумом и обозначается U. Символом  обозначается отношение принадлежности. Запись x означает , что элемент х принадлежит множеству Х. Если элемент х не принадлежит множеству Х, то пишут хХ.

Множества могут быть заданы следующими способами:

1. перечислением (списком своих элементов);

2. описанием свойств, которыми должны обладать его элементы;

3. порождающей процедурой.

ПРИМЕР

Множество экзаменационных оценок может быть задано:

1. перечислением А={2; 3; 4; 5}

2. описанием свойств: А={a a- экзаменационная оценка

3. порождающей процедурой: А=а а=2+i, i= 

Подмножеством множества А называется множество В, если любой элемент множества В принадлежит множеству А:

(1)

Символом  обозначается отношение включения. Запись АВ означает множество А является подмножеством множества В.

Не следует смешивать отношение принадлежности  и отношение включения . Отношение принадлежности применяется к элементам множества, а отношение включения к множествам. Хотя 1}, не верно, что 1, так как единственным элементом множества 1 является 1.

Если А и , то , то есть множество А строго включено в множество В. Символ  называется строгим включением.

Определение: Функцией называется однозначное отображение Х на У. Т.е. такое отображение f, что если

(х₁,y₁)  f и (х₂,y₂)  f из х₁ = х₂ следует y₁ = y₂

При этом множества Х и У могут совпадать.

Билет №9

Множества, подмножества, формула количества подмножеств конечного множества.

Множеством S называется объединение в одно целое объектов, хорошо различимых нашей мыслью или интуицией. Эти объекты называется элементами множества S. Такое интуитивное определение дал немецкий математик Г. Кантор. В данном определении важны следующие два момента:

3. Множество- это нечто, состоящее из хорошо различимых объектов.

4. Это нечто мыслится как единое целое.

Множества бывают конечными и бесконечными, Количество элементов в конечном множестве называется мощностью множества. Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается . Множество, включающее в себя в се рассматриваемые множества, называется универсальным множеством или универсумом и обозначается U. Символом  обозначается отношение принадлежности. Запись x означает , что элемент х принадлежит множеству Х. Если элемент х не принадлежит множеству Х, то пишут хХ.

Множества могут быть заданы следующими способами:

4. перечислением (списком своих элементов);

5. описанием свойств, которыми должны обладать его элементы;

6. порождающей процедурой.

ПРИМЕР

Множество экзаменационных оценок может быть задано:

4. перечислением А={2; 3; 4; 5}

5. описанием свойств: А={a a- экзаменационная оценка

6. порождающей процедурой: А=а а=2+i, i= 

Подмножеством множества А называется множество В, если любой элемент множества В принадлежит множеству А:

(1)

Символом  обозначается отношение включения. Запись АВ означает множество А является подмножеством множества В.

Не следует смешивать отношение принадлежности  и отношение включения . Отношение принадлежности применяется к элементам множества, а отношение включения к множествам. Хотя 1}, не верно, что 1, так как единственным элементом множества 1 является 1.

Если А и , то , то есть множество А строго включено в множество В. Символ  называется строгим включением.

Свойства подмножеств.

Рефлексивность. Множество А является подмножеством множества А:

. (2)

Транзитивность. Если множество А является подмножеством множества В , а множество В является подмножеством множества С, то множество А является подмножеством множества С:

(3)

Принцип объемности. Если множество А является подмножеством множества В, а множество В является подмножеством множество А, то множество А равно множеству В:

Билет №10

Множества. Операции над множествами.

1. Объединением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В:

(5)

2. Пересечением множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат множеству А и множеству В:

(6)

3. Разностью множества А и В называется множество всех тех элементов, которые принадлежат множеству А и не принадлежат множеству В:

(7)

4. Симметричной разностью множеств А и В называется множество , состоящее из элементов множества А , не принадлежащих множеству В, и элементов множества В, не принадлежащих множеству А:

(8)

5. Дополнением множества А называется множество всех тех элементов, которые не принадлежат множеству А:

(9)

Для наглядного представления операций над множествами используют диаграммы Эйлера- Венна.

Рис 1. Диаграмма Эйлера-Венна

где - это области 1,2,3

- это область 3;

- это область 1;

- это область 1,3

- это области 2,4.

Билет №11

Предикаты

Логика предикатов или исчисление предикатов – это раздел математической логики, исследующий операции над высказываниями, расчлененными на субъект и предикат.

Это расширение понятий и логических средств по сравнению с логикой высказываний или Булевой алгеброй. Логические операции с высказываниями, не разделенными на субъект и предикат – это простейший вид логических операций. «В исчислении предикатов делается дальнейший шаг анализа и разрешается рассматривать объектно–предикатную структуру простых предложений и пользоваться операциями композиции, зависящими от этой структуры», - пишет Клини.

Слово предикат (от латинского praedicatum – сказуемое), то что высказывается (утверждается или отрицается) в суждении о субъекте. Предикат выражает наличие или отсутствие того или иного признака у субъекта.

В логике предикатов под предикатом понимается некоторое свойство или отношение.

В логике предикатов, как и в логике высказываний, высказывания представляют собой или «Истину» или «Ложь». Разница в том, что в логике предикатов истинностное значение ставится в соответствие определенному предмету или группе предметов, тогда как в логике высказываний

они относились к высказыванию.

С точки зрения математики Предикат очень удобно рассматривать как функцию от некоторого числа переменных, значением которой будут логические величины.

Определение: n – местным предикатом называется логическая функция, значениями которой являются высказывания об упорядоченных множествах из n объектов, представляющих значения аргументов.

Чтобы задать n – местный предикат Р(х₁…х_N) следует указать множества D_i i=1,N - области изменения предметных переменных Х. Предикат определяется заданием подмножества М в декартовом произведении D_i. При этом Р(х₁…х_N) понимают как высказывание "упорядоченный набор (х₁…х_N) принадлежит М". Понятие предиката может еще интерпретироваться так: "Из посылок х₁…х_N, следует заключение В".

Определение: Квантор – это логическая операция, которая по предикату Р(х) строит высказывание, характеризующее область истинности предиката Р(х).

В математической логике наиболее употребительный квантор всеобщности  и квантор существования . Высказывание х Р(х) означает, что область истинности предиката совпадает с областью значения переменной х. Высказывание х Р(х) означает, что область истинности предиката не пуста.

Определение: Формула

1. Любая переменная – это формула.

2. Если А и В – формулы, то А, (АВ), (АВ), (АВ),х А, х А - формулы

Определение: Правила, по которым в логике из истинных формул образуются новые истинные формулы называются правилами вывода.

Определение: Выводом называется непустая конечная последовательность формул С₁…С_n, таких что:

• каждая С_i – есть либо посылка, либо получена из предыдущих формул по одному из правил вывода.

• Если в выводе применялись правила 5 или 7, то все формулы, начиная с последней посылки и вплоть до результата применения данного правила, исключаются из дальнейших шагов построения вывода.

Билет №12

Операции над предикатами

Для предикатов выполнимы следующие операции:

Конъюнкция - это новый предикат, который принимает значение истинно при тех и только тех значениях из вещественной области , при которых оба предиката и истинны одновременно, и ложно во всех других случаях.

Дизъюнкция - это новый предикат, который принимает значение ложно при тех и только тех значениях из вещественной области , при которых оба предиката и ложны одновременно, и истинно во всех других случаях.

Отрицание предиката - это новый предикат, который принимает значение истинно при всех из вещественной области , при которых предикат принимает значение ложно и наоборот.

Билет №13

Бинарные отношения. Рефлективность, симметричность, асимметричность, транзитивность.

Отношением называется пара вида такая, что Ф² (M²=M M),где Ф - график отношения, М - это множество, между элементами которого существует данное отношение.

1. Рефлексивность.

Отношение называется рефлексивным, если для всех x выполняется условие: xx или .

2. Симметричность.

Отношение называется симметричным , если для всех x выполняется условие: xy  yx или Ф=Ф^-1.

3. Асимметричность.

Отношение называется асимметричным, если для всех x выполняется условие: xy  yx или =.

4. Транзитивность.

Отношение называется транзитивным, если для всех x выполняется условие: xy и yz  xz или Ф ФФ.

Билет №14

Высказывания. Логические операции над высказываниями. Сложные высказывания.

Высказыванием называется повествовательное предложение, о котором можно сказать истинно оно или ложно.

1. Москва - столица России.

2. Если студент учится на отлично, то он получит красный диплом.

3. Осадки - это снег или дождь.

4. Курица – не птица.

5. Пейте томатный сок.

6. Я лгу.

7. 23<5

Высказываниями являются 1, 2, 3,4 и 7 предложения. Предложение 5 не является высказыванием, так как про него нельзя сказать истинно оно или ложно. Предложение 6 является логическим парадоксом.

Элементарным высказыванием называется высказывание, которое содержит одно утверждение (предложения 1,7).

Сложное (составное) высказывание состоит из элементарных высказываний связанных с помощью следующих предлогов и частиц: И, НЕ, ИЛИ, ЕСЛИ - ТО, ТОГДА И ТОЛЬКО ТОГДА и другие. Предложения 2,3,4 являются сложными высказываниями.

Билет №15 Равносильные высказывания.

Формулой математической логики называется сложное высказывание, которое получено из элементарных высказываний с использованием логических операций.

Две формулы равносильны, если они принимают одинаковые логические значения на любом наборе значений входящих в формулу элементарных высказываний. Равносильность формул обозначается  A  B.

Формулы равносильности.

1. Коммутативность

АVВ  ВVА А&В  В&А

2. Ассоциативность

АV(ВVС)  (АVВ)VС А&(В&С)  (А&В) &С

3. Дистрибутивность

АV(В&С)  (АVВ)&(АVС) А&(ВVС)  (А&В)V(А&С)

4. Идемпотентность

АVА  А А&А  А

5. Поглощение

АV(А&В)  А А&(АVВ)  А

6. Закон де Моргана

 &  V

7. Закон исключающий третьего

АV1  1 А&1  A

8. Закон противоречия

AV  A A&  

9. Закон двойного отрицания

 A

10.  1 ,  0

11. AB  VB

12. AB  (AB)&(BA)

13. AB  A& V &B

14. A | B   V

15. AB   &

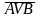
Билет №16

Таблицы истинности. Тождественно истинные и тождественно ложные высказывания.

Отрицанием высказывания х называется новое высказывание, которое истинно, если высказывание ложное и наоборот. Таблица истинности операции отрицания имеет вид:

0	1
1	0

Дизъюнкцией двух высказываний x и y (логическое «или»)называется новое высказывание, которое будет истинным тогда когда, когда хотя бы одно из высказываний будет истинным.

0	0	0
0	1	1
1	0	1
1	1	1

Конъюнкцией двух высказываний x и y (логическое «и»)называется новое высказывание, которое будет истинным тогда когда, когда оба высказывания истины. Обозначение операции конъюнкция - &(

0	0	0
0	1	0
1	0	0
1	1	1

Импликацией двух высказываний x и y («если – то») называется новое высказывание, которое ложно тогда, когда х (предпосылка) истинно, а у (следствие) ложно.

0	0	1
0	1	1
1	0	0
1	1	1

Эквивалентностью двух высказываний x и y («тогда и только тогда») называется новое высказывание, которое будет истинно , если высказывания х и у будут одновременно истинны или ложны.

0	0	1
0	1	0
1	0	0
1	1	1

Неодназночностью (суммой по модулю два) двух высказываний x и y («тогда и только тогда») называется новое высказывание, которое будет истинно тогда когда одно из высказываний х или у истинно, а другое ложно.

0	0	0
0	1	1
1	0	1
1	1	0

Штрих Шеффера (логическое «и - не») высказываний x и y - это новое высказывание, которое будет ложно тогда и только тогда когда оба высказывания истинны.

0	0	1
0	1	1
1	0	1
1	1	0

Стрелка Пирса (логическое «или - не») высказываний x и y - это новое высказывание, которое будет истинно тогда и только тогда когда оба высказывания ложны.

0	0	1
0	1	0
1	0	0
1	1	0

Для операций справедливы следующие приоритеты: , &, , , .

Тождественные высказывания. Среди высказываний особое место занимают те, в таблице истинности которых либо одни единицы, либо только нули. Это означает, что высказывание либо всегда истинно, либо ложно, независимо от истинности входящих в него высказываний. Например, высказывание всегда истинно, а высказывание всегда ложно. Доказать это можно составив таблицу истинности этих высказываний.

Сложные высказывания, истинные при любых значениях входящих в них других высказываний, называются тождественно истинными, а высказывания, ложные при любых значениях входящих в них других высказываний, называются тождественно ложными.

Тождественно истинные или тождественно ложные высказывания, если они встречаются в формулах, заменяются в них, соответственно единицей или нулем:

, .

Среди высказываний встречаются такие, таблицы истинности которых совпадают. Эти высказывания называются эквивалентными. Эквивалентными являются, например, высказывания и (то есть ).

Билет№17

Понятие отображения, понятие взаимного(биективного) отображения.

Рассмотрим два множества А и В. Элементы этих множеств могут каким-либо образом сопоставляться друг другу, образуя пары (а, b). Если задан способ такого сопоставления, то говорят что между множествами установлено соответствие. При этом совершенно необязательно, чтобы в сопоставлении участвовали все элементы множеств А и В.

Определение: Соответствием между множествами А и В называется любое подмножество R= АхВ - декартова произведения множеств.

Свойства соответствий.

1. Соответствие называется функциональным, если его график функционален.

2. Соответствие называется инъективным, если его график инъективен.

3. Соответствие называется всюду определенным, если проекция его графика на первую ось совпадает с областью отправления. Пр P₁=X.

4. Соответствие называется сюръективным, если проекция его графика на вторую ось совпадает с областью прибытия. Пр P₂=Y.

5. Соответствие называется биективным (взаимнооднозначным), если оно функционально, инъективно, всюду определенно, сюръективно.

Билет №18

Понятие обратного отображения, условие обратимости отображения.

Пусть подмножество А отображается взаимно-однозначно на множество В, т.е. f:A→B. Тогда отображение , при котором каждому элементу множества В ставится в соответствие его прообраз из множества А, называется обратным отображением для f записывается В или :В→А. Так как одному образу при биекции соответствует в точности один прообраз, обратное отображение будет определено всюду на В и однозначно. Для биекции принята запись: А

Билет №19

Элементы комбинаторики.

Комбинаторика – это раздел математики, посвященный задаче выбора и расположения элементов некоторого конечного множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения некоторой конструкции из элементов исходного множества, называемой комбинаторной конфигурацией. Можно сказать, что целью комбинаторики является изучение комбинаторных конфигураций. Это вопросы существования этих конфигураций, алгоритмы их построения, оптимизация этих алгоритмов, а так же задачи перечисления т.е. определение числа элементов данного класса.

Простейшим примером комбинаторных конфигураций являются размещения, сочетания и перестановки.

Возникновение и развитие комбинаторики тесно связано с развитием других разделов математики: теории чисел, алгебры. Еще математикам Древнего Востока была известна формула, выражающая число сочетаний через биноминальные коэффициенты и Бином Ньютона для натуральных . С мистическими целями изучались свойства магических квадратов 3-его порядка.

Комбинаторика как раздел математики появилась в трудах Блеза Паскаля и Ферма по теории азартных игр. Эти труды, составив основу теории вероятностей, одновременно содержали принципы нахождения числа комбинаций элементов данного конечного множества.

С появлением работы Лейбница и Бернулли «Искусство предположений» посвященной теории вероятностей комбинаторные схемы выделились в отдельную часть математики.

Возрождение интересов к комбинаторике относится к 50 годам ХХ века. Этот интерес связан с развитием кибернетики. Большой развивающийся раздел комбинаторики это теория блок-схем. Основные проблемы этого раздела связаны с вопросами классификации, условиями существования и методами построения некоторых классов блок-схем.

Рассмотрим множеств , содержащий по элементов соответственно. Будем выбирать по одному элементу из каждого множества и составлять новое множество. Число способов, которыми это можно сделать равно .Будем рассматривать такие множества, в которых каждый элемент входит не более одного раза. Такие соединения называются без повторений.

Будем считать, что рассматриваем множество , состоящее из n различных элементов.

Определение: Размещением без повторений из элементов по элементов называются -элементные подмножества множества , отличающиеся один от другого или самими элементами или их порядком. Обозначаем .

Теорема: Число размещений без повторений равно

Доказательство: Для того чтобы расположить элементов в определенном порядке выберем один и будем считать его «первым». Это можно сделать способами. Оставшееся множество содержит элемент. Из него выберем ещё один и будем считать его «вторым». Для выбора второго элемента существует способ. Осталось элемента. Продолжая рассуждать подобным образом понятно, что -ый элемент можно способами. Пользуясь утверждением, приведенном в начале параграфа получим

Пример: Определить, сколько трехзначных чисел можно составить из множества цифр 1,2,3,4,5 без повторений.

Решение:

Определение: Перестановками из элементов называются множества из элементов, отличающиеся один от другого порядком элементов. Обозначаем .

Теорема: Число Перестановок без повторений равно

Доказательство: Повторяет доказательство предыдущей теоремы, полагая .

Пример: К кассе за получением денег одновременно подошли 4 человека. Сколькими способами они могут выстроиться в очередь.

Решение: Очередь состоит из 4 различных человек, поэтому эти очереди отличаются только порядком элементов. Это перестановки без повторений.

Определение: Сочетаниями без повторений, содержащими элементов, выбранных из элементов заданного множества, называются всевозможные множества из элементов, отличающиеся хоть одним элементов (порядок не учитывается), при этом все элементы различны. Обозначаем

Теорема: Число

Доказательство: Рассмотрим перестановку из n элементов по . Если не считаться с порядком элементов, то существует ! Перестановок, которые не различимы. Следовательно . Упрощая эту формулу, получим искомую.

Пример: Имеется 6 штаммов бактерий. Для определения скорости их роста необходимо выбрать 3 штамма. Сколькими способами можно это сделать?

Решение: Способы отбора различаются, если каждая группа штаммов различаются хотя бы одним элементом. Это число

Пример: Выбрать из 20 человек в группе 8 человек для сдачи зачета досрочно.

Решение:

Пример: В ящике 20 шаров, среди них 12 белых, остальные зелёные. Отбирается наугад 2. Сколькими способами можно отобрать а) два белых шара, б) два зелёных, в) один белый и один зелёный.

Решение:

а)

б)

в)

Определение: Размещением с повторением из элементов по элементов называются -элементные подмножества множества , отличающиеся один от другого или самими элементами или их порядком . При этом допускается кратное вхождение элементов множества .

Теорема: Число размещений с повторениями из элементов по равно

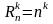
Доказательство: Рассуждения очень похожи на доказательство числа размещения без повторений. Значение, которое стоит на «первом» месте можно выбрать способами. Значение, стоящее на «втором» месте также можно выбрать способами (т.к. они могут повторяться, элементы после выбора не удаляются из множества, из которого выбирают). И т.д. процедура повторяется раз.

Определение: Сочетаниями с повторениями, содержащими элементов, выбранных из элементов заданного множества, называются всевозможные множества из элементов, отличающиеся хоть одним элементов (порядок не учитывается), при этом допускается неединичное вхождение элементов. Обозначаем

Теорема: Число

Пример: человек садятся за круглый стол. Два размещения по местам будем считать совпадающими, если каждый человек имеет одних и тех же соседей в обоих случаях. Сколько существует способов сесть за стол.

Решение: Общее число перестановок равно Но отношение соседства сохраняется при циклических перестановках (повороте) их для каждого различного размещения и при симметричном отображении (их 2). Следовательно .

Пример: Из колоды в 52 карты вынули 10 карт. В скольких случаях среди этих карт окажется а) хотя бы один туз; б) ровно один туз; в) не менее двух тузов; г) ровно два туза.

Решение:

а) Существует способов вынуть 10 карт из 52. При этом в случаях в этой выборке не окажется ни одного туза. Следовательно

б)

в) С₅₂¹⁰ – С₄₈¹⁰ – С₄¹ С₄₈⁹

г)

Пример: Сколькими способами можно посадить за круглый стол мужчин и женщин так, чтобы никакие два лица одного пола не сидели рядом.

Решение:

Выбрать места для мужчин и женщин можно двумя способами. После этого рассадить мужчин на выбранные места можно способами. На остальных местах способами можно посадить женщин. Всего способов.

Пример: Сколькими способами можно составить 3 пары из шахматистов?

Решение:

Выбираем 6 шахматистов способами. В каждой из этих выборок рассмотрим количество перестановок их 6!. Считая, что в первой паре элементы с 1 – ого и 2 – го места перестановки и т.д. Но при этом несущественен порядок в каждой паре 23 и порядок пар 3!. Следовательно, количество перестановок равно 6!/ (23 3!). Итого

Задачи:

Имеется 5 видов конвертов и 4 вида марок. Сколькими способами можно выбрать конверт с маркой?

Сколько словарей нужно издать, чтобы переводить с любого из 5 языков на любой другой?

Есть пятиразрядный цифровой замок, каждый диск которого содержит цифры от0 до 5. Сколько комбинаций таких цифр?

Сколькими способами можно упорядочить множество цифр от 1 до 2n так, чтобы все четные числа стояли на четных местах.

Сколькими способами можно упорядочить множество цифр от 1 до n так, чтобы числа 1,2,3 стояли рядом и в порядке возрастания.

Какое количество различных символов можно передать не более чем 5 знаками «.» и «-».

Автомобильные номера состоят из 3 букв и 4 цифр. Найти количество возможных номеров, если используются 32 букв русского алфавита.

Сколько машинных слов можно составить из букв слова КОЛОКОЛ, слова ВОДОРОД.

Сколькими способами 9 одинаковых конфет можно разложить по 5 пакетам, если ни один из пакетов не должен быть пустым. Тот же вопрос, но пакеты могут быть пустыми.

Билет №20

Понятие вычета по модулю N, операции над вычетами и их свойства.

Билет №21

Понятие шифрования, принцип шифров замены, шифры Цезаря и Винжера.

Шифр Цезаря является частным случаем шифра простой замены (одноалфавитной подстановки). Свое название этот шифр получил по имени римского императора Гая Юлия Цезаря, который использовал этот шифр при переписке с Цицероном (около 50 г. до н.э.).

При шифровании исходного текста каждая буква заменялась на другую букву того же алфавита по следующему правилу. Заменяющая буква определялась путем смещения по алфавиту от исходной буквы на К букв. При достижении конца алфавита выполнялся циклический переход к его началу. Цезарь использовал шифр замены при смещении К = 3. Такой шифр замены можно задать таблицей подстановок, содержащей соответствующие пары букв открытого текста и шифртекста.

Билет №22

Алгоритм RSA шифрования.

Алгоритм RSA состоит из следующих пунктов:

Выбрать простые числа p и q

Вычислить n = p * q

Вычислить m = (p - 1) * (q - 1)

Выбрать число d взаимно простое с m

Выбрать число e так, чтобы e * d = 1 (mod m)

Числа e и d являются ключами. Шифруемые данные необходимо разбить на блоки - числа от 0 до n - 1. Шифрование и дешифровка данных производятся следующим образом:

Шифрование: b = ae (mod n)

Дешифровка: a = bd (mod n)

Следует также отметить, что ключи e и d равноправны, т.е. сообщение можно шифровать как ключом e, так и ключом d, при этом расшифровка должна быть произведена с помощью другого ключа.

Билет №23

Метод математической индукции.

По своему первоначальному смыслу слово “индукция” применяется к рассуждениям, при помощи которых получают общие выводы, опираясь на ряд частных утверждений. Простейшим методом рассуждений такого рода является полная индукция. Вот пример подобного рассуждения.

Пусть требуется установить, что каждое натуральное чётное число n в пределах 4< n < 20

представимо в виде суммы двух простых чисел. Для этого возьмём все такие числа и выпишем соответствующие разложения:

4=2+2; 6=3+3; 8=5+3; 10=7+3; 12=7+5;

14=7+7; 16=11+5; 18=13+5; 20=13+7.

Эти девять равенств показывают, что каждое из интересующих нас чисел действительно представляется в виде суммы двух простых слагаемых.

Таким образом, полная индукция заключается в том, что общее утверждение доказывается по отдельности в каждом из конечного числа возможных случаев.

Иногда общий результат удаётся предугадать после рассмотрения не всех, а достаточно большого числа частных случаев (так называемая неполная индукция).

Результат, полученный неполной индукцией, остается, однако, лишь гипотезой, пока он не доказан точным математическим рассуждением, охватывающим все частные случаи. Иными словами, неполная индукция в математике не считается законным методом строгого доказательства, но является мощным методом открытия новых истин.

Пусть, например, требуется найти сумму первых n последовательных нечётных чисел. Рас-

смотрим частные случаи:

1=1=1²

1+3=4=2²

1+3+5=9=3²

1+3+5+7=16=4²

1+3+5+7+9=25=5²

После рассмотрения этих нескольких частных случаев напрашивается следующий общий вывод:

1+3+5+…+(2n-1)=n²

т.е. сумма n первых последовательных нечётных чисел равна n²

Разумеется, сделанное наблюдение ещё не может служить доказательством справедливости приведённой формулы.

Полная индукция имеет в математике лишь ограниченное применение. Многие интересные математические утверждения охватывают бесконечное число частных случаев, а провести проверку для бесконечного числа случаев мы не в состоянии. Неполная же индукция часто приводит к ошибочным результатам.

Билет №24

Перечисления (генерирования) элементов конечного множества: алгоритм перестановки.

Количество перестановок из N элементов равно N! – это известная комбинаторная формула. Прохождением всех перестановок из N элементов будем проводить «по индукции». Предположим, что мы умеем порождать все перестановки из N-1 числа. Тогда сначала сгенерируем все перестановки чисел 2, …, N, приписывая к ним слева единицу. Затем сгенерируем все перестановки чисел 1, 3, …, N, приписывая к ним слева двойку, и т. д. Последним шагом будет прохождение всех перестановок 1, …, N-1 с приписыванием к ним слева числа N.

Пример работы алгоритма для N=4:

1234

1243

1324

1342

1423

1432

2134

2143

2314

2341

2413

2431

3124

3142

3214

3241

3412

3421

4123

4132

4213

4231

4312

4321

Билет №25

Перечисления (генерирования) элементов конечного множества: алгоритм разбиения на слагаемые.

Необходимо заметить, что разбиения, отличающиеся только порядком слагаемых, мы считаем совпадающими. Назовем (N, K)- разбиениями все те разбиения числа N, для которых каждое из слагаемых не превосходит K. Пусть А (N, K) – количество таких разбиений. Числа А (N, K) будем вычислять методом динамического программирования. Для вывода рекуррентной формулы разделим все (N, K) – разбиения на два класса. В первый попадут разбиения, в которых есть слагаемые, равные K, а во второй – все остальные. Ясно, что количество разбиений во втором классе равно А (N, K-1). Найдем количество разбиений в первом. Заметим, что если из каждого разбиения этого класса выбросить одно число K(а их может быть несколько), то получим все (N-K, K) – разбиения. Следовательно верна следующая формула А(N, K)=А(N, K-1)+А(N-K, K).

Каждое разбиение единственным образом записывается в виде последовательности чисел, расположенных в порядке не возрастания. Будем порождать (N, K) – разбиения в антилексикографическом порядке, то есть порядке, обратном алфавитному.