2. Действия над векторами в координатной форме

Пусть заданы два вектора и или тоже самое

1. Равенство векторов

Два вектора и называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые длины. Из определения вектора как направленного отрезка, который можно переносить параллельно самому себе, а начало вектора перемещать в любую точку пространства, следует, что два вектора и равны тогда и только тогда, когда выполняется равенство их одноименных координат, т.е.

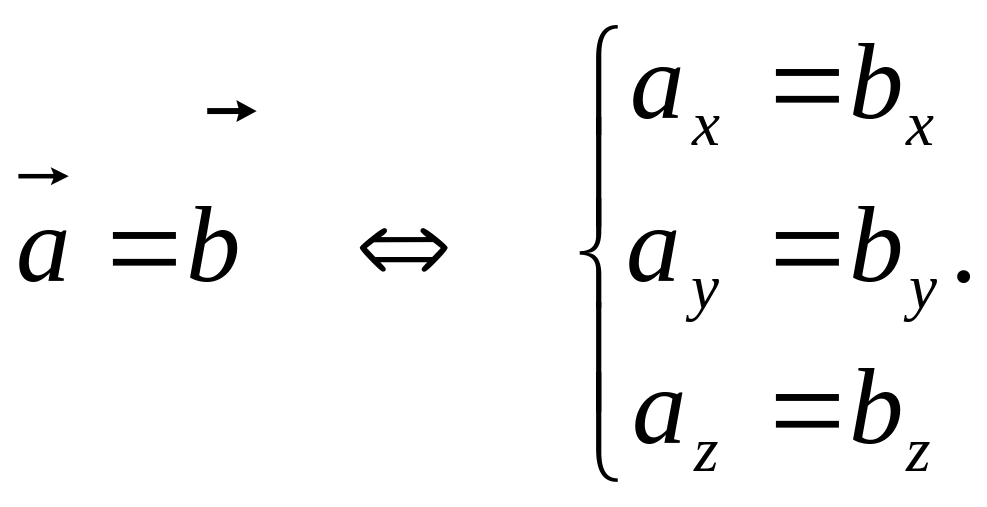
2. Линейные операции над векторами

К линейным операциям над векторами относятся сложение, вычитание и умножение вектора на число.

Суммой (разностью) векторов и называется вектор, координаты которого равны сумме (разности) одноименных координат векторов, т.е.

или .

Произведением вектора на число называется вектор, координаты которого равны произведению координат вектора на это число, т.е.

или .

Нетрудно понять, что если , то направление вектора совпадает с направлением вектора и противоположно направлению вектора , если .

3. Коллинеарность векторов.

Так как , то можно записать , где некоторое число. Для координат этих векторов будет выполнено условие:

Отсюда

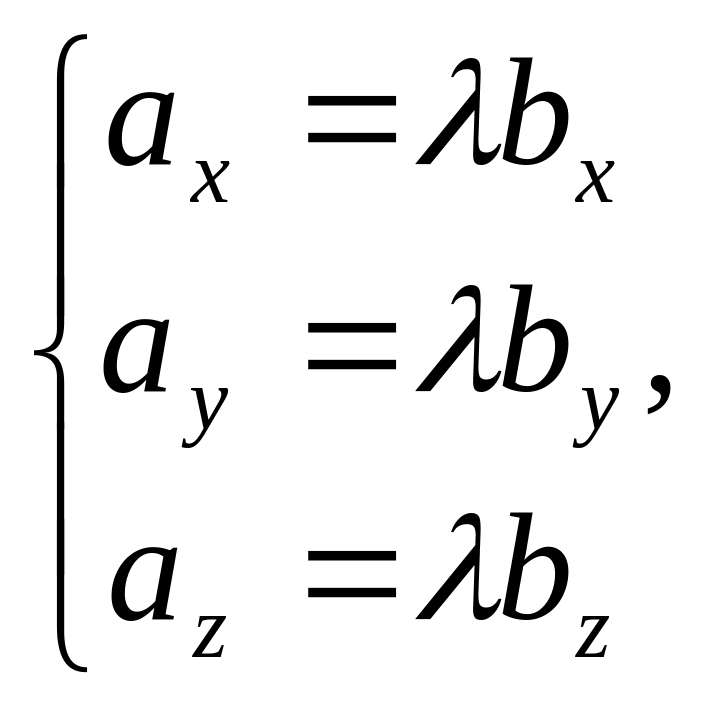т.е. или

Таким образом, справедлива теорема.

Теорема 3.1. Координаты коллинеарных векторов пропорциональны, т.е.

4. Координаты вектора

Пусть известны координаты точек и . Тогда Следовательно, координаты вектора равны разности соответствующих координат его конца и начала:

Кроме линейных операций существуют различные произведения векторов: скалярное, векторное, смешанное.

Лекция 3.2. Нелинейные операции над векторами. Линейная независимость векторов и базис пространства.

Время -2 а.ч.

План:

1. Скалярное произведение векторов и его свойства.

2. Векторное произведение векторов и его свойства

3. Линейная зависимость и линейная независимость векторов, базис

Скалярное произведение векторов

Скалярным произведением двух векторов и называется число, равное произведению длин этих векторов на косинус угла между ними. Обозначается или или . Итак, по определению

угол между векторами (За угол между векторами принимают угол между содержащими их прямыми, величина которого принадлежит промежутку ).

Приведем некоторые свойства скалярного произведения:

1) 2) 3) 4)

5) Теорема 3.2. Два ненулевых вектора и ортогональны тогда и только тогда, когда их скалярное произведение равно нулю, т.е.

Доказательство. Пусть и ортогональные вектора, значит угол между ними равен , а . Подставляя это значение в формулу скалярного произведения получим:

Пусть, наоборот, скалярное произведение двух ненулевых векторов равно нулю. Так как векторы ненулевые, то левая часть формулы может быть равна нулю только в том случае, когда косинус угла равен нулю, следовательно, этот угол равен , а значит, вектора ортогональны.

Теорема доказана.

Теорема 3.3. Если векторы и заданы своими координатами и , тогда

Данная формула легко получается, если векторы и записать и перемножить их по правилу умножения многочленов, используя очевидные равенства: