1. Множество. Способы задания множеств. Операции над множествами и их основные свойства. Декартово произведение множеств.

Множество - совокупность некоторых объектов(элементов), объединённых некоторым признаком.

Задать множество можно 2мя способами:

• перечисление элементов А={1, 2, 3};

• с помощью некоторого свойства, позволяющего определить - принадлежит ли объект к данному множеству или нет A={x : p(x)}.

Свойства:

• множества считаются равными, если они состоят из одних и тех же элементов

А = В ⇔ (А ⊆ В) & (В ⊆ А)

• Если (А ⊆ В) и (А ≠ В), то говорят, что А является собственным подмножеством В.

• Множество всех подмножеств данного множества называется булеаном Р(А)

• А ⊆ А

• А ⊆ С , C ⊆ В ⇒ А ⊆ B

• Пустое множество ∅ есть подмножество любого множества

• Число элементов множества А обозначается |А|.

Операции над множествами:

• Объединение

• Пересечение

• Разность А \ В = {x : x ∈ A & x ∉ B}

• Симметрическая разность

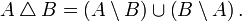
• Дополнением множества А наз. множество ¬А = U \ A

• Декартово произведение

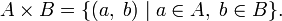
Законы:

• Коммутативность

• Ассоциативность

• Дистрибутивность

• 

• 

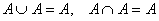
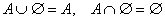
• Законы де Моргана

• Закон поглощения

А ∪ (А ⋂ В) = А

А ⋂ (А ∪ В) = А

• ¬ ¬А = А

• А \ В = А ⋂ (¬ В)

Декартовым произведением двух множеств А и В называется множество упорядоченных пар, в которых первый элемент принадлежит множеству А, а второй - множеству В.

2. Соответствия. Отображение. Обратное отображение. Сюрьективность, иньективность.

Между 2мя множествами установлено соответствие, если определено правило, оп которому для каждого элемента одного множества выбирается определённый элемент или подмножество элементов другого множества.

Отображением множества А в множество В называют соответствие, которое каждому элементу из множества А ставит в соответствие единственный элемент множества В.

Если a ∈ А - элемент множества А, то элемент множества В, который ставится ему в соответствие, обозначают f(a) , a ∈ A ↦ f(a) ∈ B.

Элемент f(a) называется значением отображения f в точке а, или образом элемента а.

При этом элемент а называется прообразом элемента f(a).

Отображение f : A → B называется сюрьекцией, если для любого элемента ∀b ∈ B его прообраз есть непустое множество

f^-1(b) ≠ ∅

Отображение f : A → B называется иньекцией, если разным элементам из множества А соответствуют разные образы.

∀a₁, a₂ ∈ А , a₁ ≠ a₂ : f(a₁) ≠ f(a₂)

Биекция - отображение, которое является одновременно сюрьекцией и иньекцией.

Если множества А и В совпадают, и f - биекция, то говорят, что А взаимно однозначно отображается на себя.

Если множество А взаимно однозначно отображается на множестве В, то

множества А и В называются эквивалентными - А В

• А А - рефлексивность

• А В ⇔ В А - симметричность

• А В, В С ⇒ А С - транзитивность

3. Понятие мощности множества. Конечные и бесконечные множества.

Мощность - число элементов конечного множества.

Конечное множество - множество, которое эквивалентно отрезку натурального ряда,

т.е. конечное множество - это такое множество, элементы которого можно пересчитать за конечное число шагов.

Бесконечное множество - множество, которое не является конечным.

Множества А и В называются равномощными, если они эквивалентны.

Бесконечные множества:

1. счётные - класс множеств, эквивалентных множеству натуральных чисел.

2. несчётные - класс множеств, не эквивалентных множеству натуральных чисел.

Счётное множество - это такое бесконечное множество, элементы которого можно пронумеровать при помощи натуральных чисел, т.е. можно указать такой способ нумерации элементов, при котором каждый элемент получит свой единственный номер.

Свойства бесконечных множеств:

1. всякое подмножество счётного множества конечно или счётно

2. всякое бесконечное множество содержит счётное подмножество

4. Принцип математической индукции.

Допустим, что

1. Установлено, что 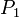  верно. (Это утверждение называется базой индукции.)

2. Для любого n доказано, что если верно 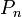 , то верно  . (Это утверждение называется индукционным переходом.)

Тогда все утверждения нашей последовательности верны.

5. Бином Ньютона.

Пусть для ∀n ∈ N существуют натуральные числа, которые обозначаются С_n⁰, С_n¹, С_n², ... , С_nⁿ.

Тогда для ∀a,b справедливо:

(a+b)ⁿ = C_n⁰ aⁿ + C_n¹ a^n-1 b + C_n² a^n-2 b² + ... + C_n^n-1 a b^n-1 + C_nⁿ bⁿ.

C_n^k = n!/k!(n-k)!

Свойства биноминальных коэффициентов:

1. C₁⁰ = C₂⁰ = C_n⁰ = 1

2. C₁¹ = C₂² = C_nⁿ = 1

3. C_n^k = C_n-1^k-1 + C_n-1^k

4. C_n⁰ + C_n¹ + C_n² + ... + C_nⁿ = 2ⁿ

5. C_n⁰ - C_n¹ + C_n² - ... + (-1)ⁿ C_nⁿ = 0

6. Мощность объединения конечных множеств (правило сложения). Принцип включения и исключения.

Правило сложения:

Пусть A и B - непересекающиеся множества, причём |A| = m , |B| = n . |A ∪ B| = m + n .

• Для ∀A,B ⇒ |A ∪ B| = |A| + |B| - |A ⋂ B|

• Для ∀A,B,C ⇒ |A ∪ B ∪ C| = |A| + |B| + |C| - |A ⋂ B| - |A ⋂ C| - |B ⋂ C| + |A ⋂ B ⋂ C|

Принцип включения и исключения:

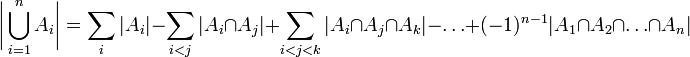
7. Мощность декартова произведения (правило произведения). Число подмножеств конечного множества.

Правило произведения:

Если А и В - конечные непересекающиеся множества, причём |A| = m , |B| = n , то

|A x B| = m x n .

Пусть М - конечное множество, состоящее из n элементов, тогда множество всех подмножеств данного множества состоит из 2ⁿ элементов

|P(M)| = 2ⁿ

8. Число перестановок конечного множества с повторениями и без повторений.

Перестановки с повторениями:

P =

9. Число размещений с повторениями и без повторений.

10. Число сочетаний с повторениями и без повторений.

11. Упорядоченные разбиения множеств. Неупорядоченные разбиения множеств.

Разбиение множества — это представление его в виде объединения произвольного количества попарно непересекающихся подмножеств.

Пусть   — произвольное множество. Семейство непустых множеств  ,

где   — некоторое множество индексов (конечное или бесконечное),

называется разбиением  , если:

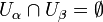1.  для любых 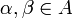 , таких что  ;

2. .

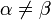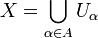При этом множества   называются блоками или частями разбиения данного множества  .

12. Полиномиальная формула.

Формула (х₁+х₂+…+х_k)ⁿ=

называется полиномиальной, где суммирование выполняется по всем решениям уравнения n₁+n₂+ …+ n_k = n в целых неотрицательных числах, n_i 0, I =1,2,…,k.

Для доказательства выполним умножение

(х₁+х₂+…+х_k)·(х₁+х₂+…+х_k) … (х₁+х₂+…+х_k) = (х₁+х₂+…+х_k)ⁿ.

n

Чтобы привести подобные в полученном выражении, необходимо подсчитать количество одночленов вида каждого разбиения n₁+n₂+ …+ n_k = n. Для получения же одночлена необходимо выбрать х₁ в качестве множителя в n₁ скобках при раскрытии выражения (х₁+х₂+…+х_k)ⁿ. Это можно сделать способами. Из оставшихся n – n₁ не раскрытых скобок необходимо выбрать х₂ в качестве множителя в n₂ скобках. Это можно сделать способами и т.д. Тогда количество одночленов при раскрытии выражения

(х₁+х₂+…+х_k)·(х₁+х₂+…+х_k) … (х₁+х₂+…+х_k)

n

будет равно числу … = упорядоченных разбиений.