Пример.

1. Давление газообразного вещества зависит от двух переменных. Для одного моля идеального газа имеем

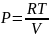
Тогда

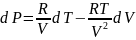
и

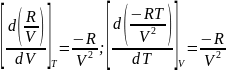
2. Определите тип приведенных дифференциальных уравнений

A. 2xydx + x²dy

Б. xydx + x²dy

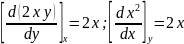
Для выражения “Б” имеет место неравенство x  2x.

Таким образом “А” – полный, “Б” – неполный дифференциал

dz = 2xydx + x²dy

Ф = xydx + x²dy.

Для интегрирования дифференциального выражения в форме полного дифференциала необходимо задать путь интегрирования или с математической точки зрения кривую интегрирования AB, которая связывает между собой переменные x и y. Здесь A и B – точки начала и конца интегрирования. При задании кривой интегрирования криволинейный интеграл

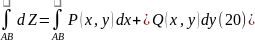
переходит в определенный интеграл. Хотя математическая форма подынтегрального выражения зависит от вида функциональной зависимости y = (x). Математическое выражение самой функции z как суммы первообразной и постоянной интегрирования от пути интегрирования не зависит.

В наиболее простом варианте кривую интегрирования можно выразить в виде совокупности прямолинейных отрезков на поверхности x, y, например, в таком виде (рис. 4)

а) x₀y₀-xy₀-xy или б) x₀y₀-x₀y-xy

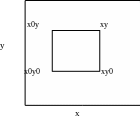
Рис. 4 Пути интегрирования полного дифференциала

Интегрируем уравнение () по x от x₀ до x при любом фиксированном значении y, например y₀. При фиксированном значении y второе слагаемое в уравнении становится равным нулю. Тогда

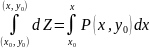
или

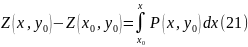
Теперь интегрируем (20) по y от y₀ до y при любом фиксированном значении x, кроме x₀. В этом случае имеем

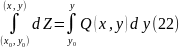
или

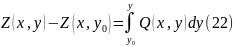
Искомая функция в виде приращения Z есть сумма (21) и (22)

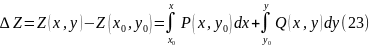
Саму функцию Z(x,y) в виде суммы первообразной и постоянной интегрирования можно найти по уравнению

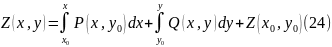
Второй член постоянной интегрирования одержит в неявном виде в интегральных членах уравнения (24).

Аналогичное выражение можно получить интегрируя (20) по пути “б”.

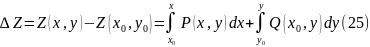
или

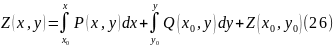
Уравнения (23) и (25) отражают важные свойства криволинейного интеграла от полного дифференциала: приращение Z (в физическом смысле изменение) и математический вид Z не зависят от пути интегрирования. Приращение (величина) Z однозначно определяется координатами точек конца и начала кривой интегрирования – (x₀,y₀ и x,y). Это заключение и есть математическое воплощение основной характеристики свойства системы (функции состояния): его изменение не зависит от пути процесса и определяется только параметрами системы в конце и начале процесса.

Пример.

1. Найти Z и функцию Z, интегрируя выражение dz = 2xydx + x²dy по пути “а” и “в”.

В соответствии с уравнениями (23), (25) имеем

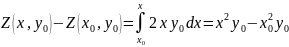
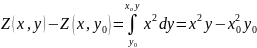
∆Z = Z(x,y) + Z(x,y₀) – Z(x,y₀) – Z(x₀,y₀) = x²y + x²y₀ – x²y₀ – x₀²y₀

или

∆Z= Z(x,y) – Z(x₀y₀) = x²y – x₀²y₀ (27)

Для функции Z находим

Z(x,y) = x²y + Z(x₀,y₀) – y₀²y₀

или

Z(x,y) = x²y + С (28)

где (Z(x₀,y₀) – x₀²y₀) – константа интегрирования С₀

Используя уравнение (25) (путь “б”) получаем

Z(x,y) – Z(x₀,y₀) = x₀²y – x₀²y₀ + a²y – x₀²y

Z(x,y) – Z(x_0,y₀) = x²y – x₀²y₀

или

Z(x,y) = x²y + C

Из выражений (27,28) следует, что как математическое выражение функции так и ее изменение не зависят от пути интегрирования.