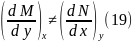Физические величины как свойство системы и как функции процесса

Прежде чем рассмотреть этот вопрос напомним*, что интегрированием дифференциала

d(y) = f(x)dx (1)

функциональную зависимость y(x) находят в виде суммы первообразной F(x) и постоянной С

y = F(x) + C (2)

Чтобы найти y в явном виде, необходимо задать начальные условия. Примем, что при значении x = х₀ y имеет значение равное y₀, что приводит к уравнению

y ₀ = F(x₀) + C,

из которого следует, что

С = y₀ – F(x₀)

В этом случае для функции y(x) имеем

y = F(x) + y₀ – F(x₀) (3)

Необходимость нахождения функции y(x) в виде уравнения (3) следует из очевидных соображений, которые рассмотрим на простом примере

dy = adx (4)

где а – постоянная величина.

Если в уравнении (2) ограничиться только одним членом в виде первообразной, будет иметь место частный вариант

y = F(x) = ax (5)

Однако существует множество других функций y = ax + C, которые удовлетворяют уравнению (1).

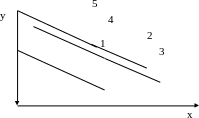
Условием y = y₀ при х = х₀ как раз и задается все это множество функций (6), включая и ту, которая выражается уравнением (5), рис. 1.

y(x) = ax + y₀ – ax₀ (6)

_____________________

^*Математические сведения, приведенные в этом разделе излагаются, например, Г.М. Фихтенгольц. Курс дифференциального и интегрального исчисления т II, III, 1970, стр.11 – 19, 225– 256 и 41 – 74 соответственно. В этих же разделах рассматриваются некоторые задачи, имеющие важное значение в курсе физической химии.

Рис 1. Часть множества функций, удовлетворяющих уравнению (6)

Какое значение придать y₀ при x = x₀ зависит от физического смысла конкретной задачи. Из рис 1 следует также, что задание условий «y₀ при х = х₀» означает задание точки отсчета для функций, в физической химии – задание начального состояния.

Пример.

Известно, что дифференциал скорости движения тела под действием силы тяжести имеет вид

dV = gdt (7)

Найти V(t) и приращение ΔV при начальных условиях:

а) t = 0; V = 0;

б) t = t₀; V = V₀

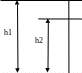
Рис. 2 Путь движения тела при разных начальных условиях

Решение.

Исходя из уравнения (2) находим

V = gt + C (8)

где

C = V₀ – gt₀ (9)

При начальных условиях «а» постоянные интегрирования равны нулю и V = gt. В этом случае тело начинает движение с высоты h₁, причем в исходном состоянии оно находилось в покое.

При начальных условиях «б»

С = V₀ – gt₀

V = gt + V₀ – gt₀

где V₀ – скорость движения тела в момент времени t₀, или

V = V₀ + g(t – t₀) (10)

При условии «б» начальным состоянием было состояние, в котором тело в момент времени t₀ имело скорость V₀, продолжая движение с высоты h₂.

Уравнение (3) можно найти несколько иным путем, а именно интегрируя уравнение (1) при постоянных нижних пределах x₀, y₀ и переменных верхних пределах х и y

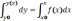
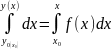
Δy = y(x) – y₀(x₀) = F(x) – F(x₀) (11)

В этом случае интегрирование дает приращение функции y(x) (11), из выражения которого находят y(x)

y = F(x) + y₀(x₀) – F(x₀)

где y₀(x₀) – F(x₀) – постоянная интегрирования.

В дальнейшем мы будем часто использовать этот способ как для нахождения самой функции y(x), так и её приращения.

Пример.

Определить в общем виде изменение энтропии при нагревании одного моля азота от температуры Т₀ до произвольной температуры Т при постоянном давлении Р₀ = 1атм, если известно, что теплоемкость N₂ постоянная величина и равная 7/2R. Найти уравнение, которое описывает зависимость энтропии N₂ от температуры, если мольная энтропия при 298,15К и давлении 1атм (S⁰) равна 191,5 Дж/моль·К. Рассчитать изменение энтропии N₂ при его нагревании от 298,15 до 398,15 К.

Решение.

Известно, что зависимость энтропии чистых веществ от температуры при постоянном давлении в дифференциальной форме выражается уравнением

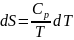
где С_р – мольная изобарная теплоемкость.

Интегрируя последнее уравнение по способу, выражаемому соотношением (11), находим

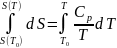
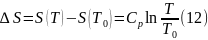
или

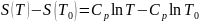
Отсюда следует, что зависимость S = f (T) в общем виде выражается уравнением

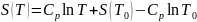
где 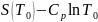– постоянная интегрирования.

Имея в виду, что для азота S(T₀) = S⁰ и равна 191,5 Дж/моль·К, находим

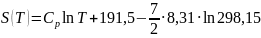
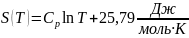(13)

Из уравнения (13) можно непосредственно убедиться, что S⁰ при температуре 298,15 К, равное 191,5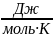 , действительно является точкой отсчета зависимости S = f (T), рис. 3.

S

191,5

398,15

348,15

298,15

T

Рис. 3 Зависимость энтропии N₂ от температуры при Р₀ = 1атм

Для изменения энтропии при повышении температуры от 289,15 до 398,15 К в соответствии с уравнением (12) получаем

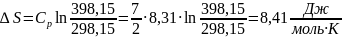(14)

Как отмечалось выше физические величины, изменение которых не зависит от пути процесса, называются свойствами системы. С математической точки зрения свойство системы является функцией параметров, определяющих ее состояние. Поэтому вместо термина свойство системы обычно используется выражение функция состояния или точнее функция параметров состояния.

Энтропия чистого вещества при Р = const является функцией только одной переменной – температуры. Как видно из уравнений (), () ее изменение действительно определяется значением температуры в начале и конце процесса.

Рассмотрим, как находят изменение свойства системы, когда оно зависит от двух параметров. Кроме того выясним различие между полным и неполным дифференциалом и какое отражение оно находит применительно к физическим величинам.

Пусть Z – свойство или в математическом смысле функция двух переменных

Z = f (x,y)

В этом случае дифференциальный формой Z является полный дифференциал

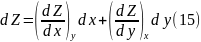
Поскольку частные производные в свою очередь суть функции x, y введем обозначения

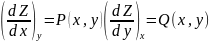
Тогда dz = P(x, y)dx + Q(x, y)dy (16)

Для таких величин как теплота и работа дифференциальной формой является неполный дифференциал. В общем случае неполный дифференциал некоторой величины Ф

Ф = M(x, y)dx + N(x, y)dy (17)

Выражение Ф отличается от полного дифференциала тем, что хотя дифференциальные коэффициенты M(x,y) и N(x,y) являются определенными функциями от x, y, сами величины Ф в виде функции от x, y выразить нельзя. Другими словами, не существует такой функции Ф переменных x, y, для которой выражение (17) было бы полным дифференциалом.

Неполный дифференциал может иметь вид

M(x, y)dx или Ф = N(x, y)dy, (17a)

если x и соответственно y, имеют произвольные фиксированные значения. Именно такую дифференциальную форму имеет любая физически возможная работа, в частности объемная:

δW = PdV

Дифференциальное выражение является полным дифференциалом, если выполняется условие равенства смешанных производных

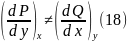
В случае неполного дифференциала смешанные производные не равны между собой