17. Расчет средней ошибки аппроксимации

Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии т.е у и ỹх. Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, это лучшее качество модели. Величина отклонений фактических и расчетных значений результативного признака(y-ỹх) по каждому наблюдению представляет собой ошибку аппроксимации. Их число соответствует объему совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Для сравнения используются величины отклонений, выраженные в процентах к фактическим значениям.

Поскольку ( y-ỹх) может быть как величиной положительной так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.

Отклонения ( y-ỹх) можно рассматривать как абсолютную ошибку аппроксимации, а

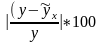
как относительную ошибку аппроксимации. Что б иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации как среднюю арифметическую простую:

18. Анализ вариации зависимой переменной в регрессии

После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.

Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т. е. b=0, и, следовательно, фактор х не оказывает влияния на результат у.

Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от среднего значения у на две части – «объясненную» и «необъясненную».

+ ,

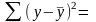
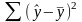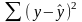TSS RSS ESS

где TSS – общая сумма квадратов отклонений;

RSS – сумма квадратов отклонений, объясненная регрессией;

ESS – остаточная сумма квадратов отклонений.

Условно разделим всю совокупность причин на две группы: изучаемый фактор х и прочие факторы. Если фактор не оказывает влияния на результат, то линия регрессии на графике параллельна оси ОХ и среднее значение у равно оценке (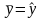 ). Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадет с остаточной (TSS=ESS). Если же прочие факторы не влияют на результат, то у связан с х функционально и остаточная сумма квадратов равна нулю (ESS). В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов (TSS=RSS).

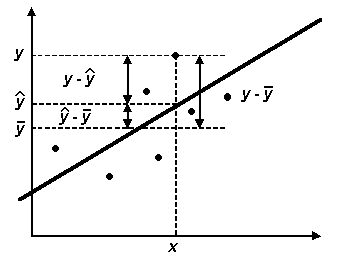
20. Гомоскедастичность и гетероскедастичность дисперсии остатков

Условие независимости дисперсии ошибки от номера наблюдения (от регрессора x_i): Е(_i ²) = Var(_i) = ². i = l,...,n. называется гомоскедастичностъю (homoscedasticity); случай, когда условие гомоскедастичности не выполняется, называется гетероскедастичностъю (heteroscedasticity). На рис. 7.2а приведен пример типичной картинки для случая гомоскедастичности ошибок; на рис. 7.26 — пример данных с гетероскедастичными ошибками (возможно, что в этом примере Var (_i) ~ x_i²).

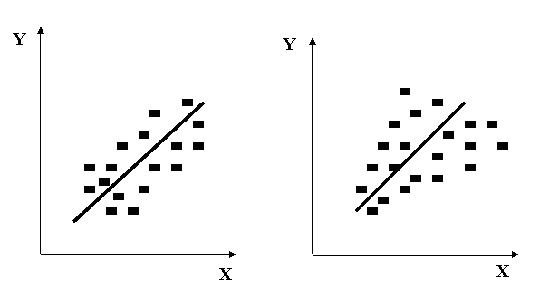
Рис 7.2а Рис. 7.2б

Условие Е(_i _j)= 0 при i ≠ j указывает на некоррелированность ошибок для разных наблюдений. Это условие часто нарушается в случае, когда наши данные являются временными рядами. В случае, когда это условие не выполняется, говорят об автокорреляции ошибок (serial correlation).

Для проверки случайного характера остатков _j , строится график их зависимости от теоретических значений результативного признака. Если на графике получена горизонтальная полоса, то остатки представляют собой случайные величины и МНК оправдан, теоретические значения хорошо аппроксимируют фактические значения y_i.

Возможны следующие случаи, если _j зависит от , то:

• Остатки _j не случайны (рис 7.3а)

• Остатки _j не имеют постоянной дисперсии (рис. 7.3в)

• Остатки _j носят систематический характер (рис. 7.3б)

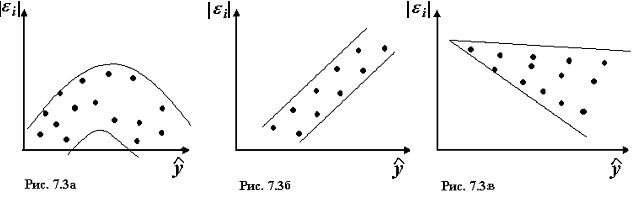
В таких случаях необходимо либо применять другую функцию (например, вводить кусочно-линейные- модели), либо вводить дополнительную информацию и заново строить уравнение регрессии до тех пор, пока остатки не будут случайными величинами.

Предпосылка о нормальном распределении остатков позволяет проводить проверку параметров регрессии с помощью критериев t, F.

Тем не менее, нарушение этого условия не оказывает решающего действия на свойства оценок регрессии, найденных с применением МНК.