Билет 1

1. Основные понятия теории принятия решений.

Под принятием решений будем понимать особый процесс человеческой деятельности, направленный на выбор наилучшего варианта действий.

Понятия:

1. Люди

   1. ЛПР - лицо принимаюшее решение - непосредственно человек

   2. Владелец проблемы - человек,который по мнению окружающих должен решить проблему.

   3. Участник активной группы — группы людей, имеющих общие интересы и старающихся оказывать влияние на процесс выбора и его результаты.

1. Альтернативы

   1. Независимые. Независимыми являются те альтернативы, любые действия с которыми (удаление из рассмотрения, выделение в качестве единственно лучшей) не влияет на качество других альтернатив.

   2. Зависимые. При зависимых альтернативах оценки одних из них оказывают влияние на качество других.

1. Критерии. Варианты решений характеризующиеся различными показателями и их привлекательностью для ЛПР называются признаками, факторами, атрибутами или критериями.

   1. Зависимые. Зависимыми называются те критерии, при которых оценка альтернативы по одному из них определяет (однозначно или с большой степенью вероятности) оценку по другому критерию.

   2. Независимые.

1. Шкалы

   1. Количественные

      1. Абсолютная

      2. Отношений

      3. Интервалов

      4. Разностей

   2. Качественные

      1. Номинальнве

      2. Порядковые

      3. Вербально-числовые (шкала Харрингтона)

2. Суть некритериального сравнения альтернатив. Метод попарного сравнения.

В пособии эта тема называется «выбор наилучшего решения из эффективных «паретовских» решений. Суть: есть множество возможных решений, среди которых есть такие, что все критерии для первого решения больше или равны критериям второго.

Пример:

W(B₁) = (y₁₁, y₁₂, y₁₃, y₁₄) = (1, 0, 0,1);

W(B₂) = (y₂₁, y₂₂, y₂₃, y₂₄) = (0.57, 1, 0.5, 0);

W(B₃) = (y₃₁, y₃₂, y₃₃, y₃₄) = (0.5, 0.67, 0.75, 1);

W(B₄) = (y₄₁, y₄₂, y₄₃, y₄₄) = (0.14, 0.33, 0.25, 1);

W(B₅) = (y₅₁, y₅₂, y₅₃, y₅₄) = (0, 1, 0, 0).

Например, сравнение варианта 3 и варианта 4, показывает, что по первым двум показателям третий вариант превосходит четвертый, однако по третьему показателю условие превосходства не выполняется:

W(B₃) ∼ W(B₄) → y₃₁ > y₄₁, y₃₂ > y₄₂, y₃₃ > y₄₃, y₃₄ = y_44.

Другую ситуацию имеем при сравнении варианта 2 и варианта 5:

W(B₂) ∼ W(B₅) → y₂₁ > y₅₁, y₂₂ > y₅₂, y₂₃ > y₅₃, y₂₄= y_54.

Очевидно, что в составе множества решений нет смысла оставлять вариант 4 и 5, так как они не представляются перспективным, и поэтому эти варианты вытесняются или, как говорят, «доминируются», соответственно вариантами 2 и 3. Варианты 4 и 5 являются неконкурентоспособными. В результате описанной процедуры отбрасываются непригодные варианты (решения), множество оставшихся решений уменьшается, и в нем сохраняются так называемые «эффективные», или «паретовские», решения, характерные тем, что ни у одного из них не существует доминирующего решения. Анализ действительных вариантов возможных решений деловой игры показывает, что такими «паретовскими», недоминируемыми, вариантами являются все пять вариантов — B₁, B₂, B₃, B₄, В₅ (см. табл. 5.3.2.). В приведенном примере множество возможных решений не сократилось, но возможны задачи, в которых число неэффективных вариантов может быть значительно больше.

Таким образом, множество Парето содержит только те варианты, которые не доминируются другими вариантами.

Билет 2

1. Аксиомы рационального поведения.

В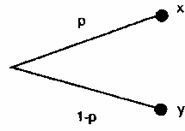 [1] вводится шесть аксиом и доказывается существование функции полезности. Дадим содержательное представление этих аксиом. Обозначим через х, у, z различные исходы (результаты) процесса выбора, а через р, q - вероятности тех или иных исходов. Введем определение лотереи. Лотереей называется игра с двумя исходами: исходом х, получаемым с вероятностью р, и исходом у, получаемым с вероятностью 1-р (рис. 2.1).  

Рис.2.1. Представление лотереи  

Примером лотереи является подбрасывание монеты. При этом, как известно, с вероятностью р = 0,5 выпадает орел или решка. Пусть х = $10 и у = - $10 (т. е. мы получаем $10 при выпадении орла и платим столько же при выпадении решки). Ожидаемая (или средняя) цена лотереи определяется по формуле рх+(1-р)у.

Приведем аксиомы рационального выбора.

Аксиома 1. Исходы х, у, z принадлежат множеству А исходов.

Аксиома 2. Пусть Р означает строгое предпочтение (похожее на отношение > в математике); R — нестрогое предпочтение (похожее на отношение ³); I — безразличие (похожее на отношение =). Ясно, что R включает Р и I. Аксиома 2 требует выполнения двух условий:

1) связности: либо xRy, либо yRx, либо то и другое вместе;

2) транзитивности: из xRy и yRz следует xRz.

Аксиома 3. Две представленные на рис. 2.2 лотереи находятся в отношении безразличия.            

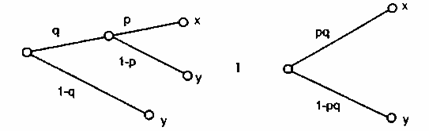
Рис. 2.2. Две лотереи, находящиеся в отношении безразличия  

Справедливость этой аксиомы очевидна. Она записывается в стандартном виде как ((х, р, y)q, y)I (x, pq, у). Здесь слева представлена сложная лотерея, где с вероятностью q получаем простую лотерею, в которой с вероятностью р получаем исход х или с вероятностью (1—р) — исход у), и с вероятностью (1—q) — исход у. Аксиома 4. Если xIy, то (х, р, z) I (у, р, z). Аксиома 5. Если хРу, то хР(х, р, у)Ру. Аксиома 6. Если xPyPz, то существует вероятность р, такая, что у!(х, р, z). Все приведенные выше аксиомы достаточно просты для понимания и кажутся очевидными. В предположении, что они выполняются, была доказана следующая теорема [1]: если аксиомы 1—6 удовлетворяются, то существует числовая функция полезности U, определенная на А (множество исходов) и такая, что: 1) xRy тогда и только тогда, когда U(x) > U(y). 2) U(x, р, у) = pU(x)+(l-p)U(y). Функция U(x) — единственная с точностью до линейного преобразования (например, если U(x) > U(y), то и a+U(x) > > a+U(y), где а - целое положительное число).

2. Сущность многокритериального выбора.

Это такие задачи, где для оценки альтернатив нужно выбрать несколько факторов, т е критериев. Таких задач много.

Многокритериальные задачи можно решать путем сравнения многокритериальных альтернатив и для этого можно выбрать один из предлагаемых в п. 5.4 способов. Однако для того, чтобы ими воспользоваться, необходимо предварительно того, чтобы ими воспользоваться, необходимо предварительно решить следующие задачи:

– определить приоритеты или коэффициенты относительной важности частных показателей;

– определить правила или приемы сведения всей совокупности показателей к единой шкале для случая, если среди частных показателей встречаются и количественные, и качественные, а также разные по размерности показатели.

Билет 3