
- •Глава 1. Основные понятия
- •§1 Операции над комплексными числами
- •§2 Комплексная плоскость
- •§3 Некоторые понятия, относящиеся ко множествам. Кривые на комплексной плоскости.
- •§4 Функции комплексного переменного
- •§5 Функциональные последовательности и ряды
- •§6 Степенные ряды
- •Глава 2. Аналитические функции. Конформные отображения.
- •§1 Аналитические функции
- •§2 Конформные отображения
- •Глава 3. Примеры конформных отображений
- •§1 Дробно линейное отображение
- •§3 Функция
- •§4 Функция Жуковского
- •§7 Таблица некоторых конформных отображений.
- •Глава 4. Теория интеграла
- •§1. Понятие интеграла. Теорема Коши.
- •§2 Интеграл Коши
- •§3 Первообразная.
- •Глава 5. Ряды Тейлора и Лорана
- •§1 Ряд Тейлора аналитической функции
- •§2 Единственность аналитической функции. Принцип максимума модуля.
- •§3 Ряды Лорана
- •§4 Изолированные особые точки однозначных аналитических функций.
- •Глава 6. Элементы теории вычетов и их использование при вычислении интегралов
- •§1 Вычеты
- •§2. Вычисление интегралов
- •§3 Простейшие классы аналитических функций.
- •Глава 7. Преобразование Лапласа.
- •§1 Преобразование Лапласа.
- •§2 Свойства преобразования Лапласа
- •Глава 8. Приложения.
- •§1 Комплексный потенциал
- •§2 Операционное исчисление
Глава 1. Основные понятия
§1 Операции над комплексными числами
Основные понятия, связанные с комплексными числами изучались в первом семестре. Перечислим некоторые из них.
Алгебраическая
форма
записи комплексного числа:
![]() – вещественная
часть,
– вещественная
часть,
![]() -
мнимая часть комплексного числа.
Тригонометрическая
форма
записи (представление числа в
экспоненциальной форме):
-
мнимая часть комплексного числа.
Тригонометрическая
форма
записи (представление числа в
экспоненциальной форме):
![]() ,
r
–модуль
комплексного числа. Выражение
,
r
–модуль
комплексного числа. Выражение
![]() пока рассматривается, как сокращенная
запись суммы
пока рассматривается, как сокращенная
запись суммы
![]() .
Легко проверяется, что
.
Легко проверяется, что
![]() ,
в частности,
,
в частности,
![]() Далее:
Далее:
![]() -
аргумент комплексного числа.
-
аргумент комплексного числа.
Главное
значение аргумента обозначается:
![]() и
выбирается в диапазоне
и
выбирается в диапазоне
![]() .
.
Аргумент
комплексного числа:
![]()
слайд 43 (модуль комплексного числа)
слайд 44 (аргумент комплексного числа)
Сопряженное
число
![]() .
Отметим два свойства сопряжённых чисел:
.
Отметим два свойства сопряжённых чисел:
![]()
слайд 24 (сложение комплексных чисел)
слайд 28 (умножение комплексных чисел)
слайд 27 (комплексное сопряжение)
Формула
Бинома Ньютона: для любых комплексных
чисел a,b
и натурального n
справедливо
равенство
 .
.
На рис. 1.1 приводится геометрическая интерпретация комплексного числа.

Рис. 1.1
slide 1 1
Расстояние
между комплексными числами
![]() (рис.
1.2)
(рис.
1.2)

Рис. 1.2
slide 1 2
Пример:
Множество
![]() представляет собой геометрическое
место комплексных чисел, сумма расстояний
которых до
представляет собой геометрическое
место комплексных чисел, сумма расстояний
которых до
![]() и -1 равна 2. Это множество представляет
собой эллипс с фокусами в
и -1.
и -1 равна 2. Это множество представляет
собой эллипс с фокусами в
и -1.
Возведение
в степень, формула Муавра: если
![]() , то
, то
![]()
slide42 (формула Муавра)
Извлечение
корней: если
![]() ,
то
,
то
![]()
Здесь
под
![]() понимается
арифметическое значение корня.
понимается
арифметическое значение корня.
slide2 (извлечение корней)
§2 Комплексная плоскость
Множество
комплексных чисел удобно интерпретировать
как плоскость, которую называют
комплексной
плоскостью
и обозначают C,
комплексное число – это точка на этой
плоскости. Можно рассматривать комплексное
число, как радиус вектор, тогда операции
сложения комплексных чисел совпадают
с операциями сложения векторов (радиус
векторов). К комплексной плоскости
формально добавляется абстрактная,
«несобственная» точка - бесконечность
![]() .
Комплексная плоскость С
с добавленной к ней несобственной
«бесконечно
удаленной
точкой»
называется расширенной
комплексной плоскостью
и обозначается
.
Комплексная плоскость С
с добавленной к ней несобственной
«бесконечно
удаленной
точкой»
называется расширенной
комплексной плоскостью
и обозначается
![]() .
Геометрически бесконечно удаленную
точку можно интерпретировать с помощью
сферы Римана.
.
Геометрически бесконечно удаленную
точку можно интерпретировать с помощью
сферы Римана.
Рассмотрим сферу S, касающуюся комплексной плоскости в точке (0,0). Между точками сферы S и точками расширенной комплексной плоскости устанавливается взаимнооднозначное соответствие, как показано на рисунке.

Рис. 1.3. Стереографическая проекция (сфера Римана)
Именно, из верхнего полюса сферы проводится луч, соединяющий точку сферы A с некоторой точкой B плоскости. Самому полюсу P соответствует бесконечно удаленная точка . Эта сфера называется сферой Римана. Такое отображение для случая сферы радиуса 1 задается следующими функциями:
![]() .
.
Для
доказательства, рассмотрим полярные
координаты (см. Рис. 1.3):
 тогда
тогда
 ,
откуда получим:
,
откуда получим:
 .
.
|
|
Рис. 1.4.
Можно показать, что прямые и окружности из переходят в окружности на S, а углы между пересекающимися кривыми сохраняются.
Комплексная плоскость с ранее введенным расстоянием представляет собой евклидово пространство. Перечислим основные понятия и определения, связанные со сходимостью.
Расстояние
между комплексными числами
![]()
Окрестность
точки
![]()
Окрестность
бесконечно удалённой
точки :
![]()
Проколотая
окрестность
точки
![]()
Сходимость, предел последовательности:
![]() означает,
что
означает,
что
![]()
Необходимое и достаточное условие сходимости для случая, когда предельная точка не равна бесконечности:
![]()
Критерий Коши сходимости последовательности к конечному пределу (в С) :
![]()
![]()
Множество
комплексных чисел является линейным
пространством. Наличие метрики и операций
линейного пространства позволяет ввести
понятие числового ряда. Комплексный
ряд
![]() с
общим членом
с
общим членом
![]() определяется,
как
определяется,
как
 .
В случае сходимости обоих действительных
рядов
.
В случае сходимости обоих действительных
рядов
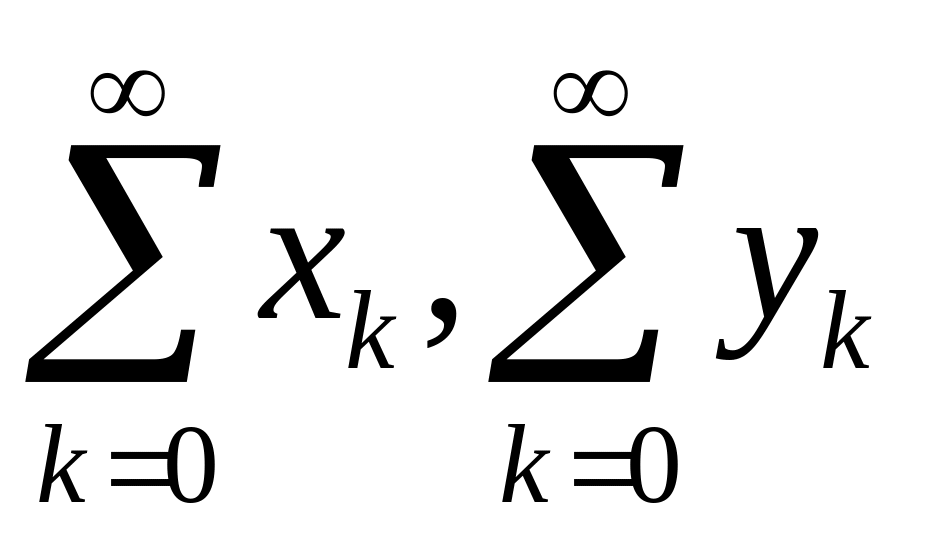 получаем
комплексное число – сумму этого ряда.
Таким образом, изучение комплексного
ряда сводится к изучению двух вещественных
рядов. Наиболее важными свойствами
рядов, используемых в дальнейшем,
являются: абсолютная сходимость, свойства
суммы, разности рядов, перестановка и
перемножение абсолютно сходящихся
рядов.
получаем
комплексное число – сумму этого ряда.
Таким образом, изучение комплексного
ряда сводится к изучению двух вещественных
рядов. Наиболее важными свойствами
рядов, используемых в дальнейшем,
являются: абсолютная сходимость, свойства
суммы, разности рядов, перестановка и
перемножение абсолютно сходящихся
рядов.


