15 Определение расположения квп по отношению к исходной системе координат.

В данном разделе приведены алгоритмы приведения уравнений кривых второго порядка к каноническому виду и определения расположения канонической системы координат по отношению к исходной.

Пусть дано общее уравнение кривой второго порядка  . Находим инварианты кривой второго порядка: . В случае если   находим еще инвариант По полученным инвариантам определяем тип кривой второго порядка. Возможны следующие случаи:

1. Центральные кривые  .

(a) Составляем характеристическое уравнение   и находим его корни   и   ,причем если  , то   ; a если  , то   тот корень знак которого совпадает со знаком  .

(b) Составляем уравнение кривой в канонической системе координат

(c) Находим центр   кривой, решая систему

(d) Находим главные направления  , которые являются направляющими векторами канонических осей. Подставляя в уравнение   вместо   и   соответственно   и   получаем равенство

 которое можно записать в виде

Следовательно имеем пропорциональность строк этого определителя, т.е.

 или

Поскольку эта система однородная, а вектор   ненулевой, то определитель этой системы должен быть нулевым, т.е.

 .

Таким образом, корням характеристического уравнения соответствуют главные направления кривой второго порядка, определяемые системой  , причем  , а  .

(e) Строим кривую в системе координат   по каноническому уравнению,где

2. Парабола  . (a) По инвариантам составляем уравнение параболы

(здесь знак перед радикалом выбирается противоположным знаку  ).

(b) Находим ось параболы 

(c) Находим вершину параболы   из системы

(d) Из уравнения оси параболы находим направляющий вектор   этой прямой. Если  , то

Если  , то

(e) Строим параболу по каноническому уравнению в системе  . 3. Вырожденный случай  . (a) По инвариантам составляем уравнение

(b) Находим уравнение оси абсцисс канонической системы   или  .

(c) Выбираем произвольно начало системы координат   (любая точка лежащая на прямой из предыдущего пункта)

(d) Находим направляющий вектор оси абсцисс  .Тогда

(e) Строим линию по ее каноническому уравнению в системе  .

16 Уравнение квп в аффинной системе координат.

ТЕОРЕМА 16.1. Пусть относительно аффинной системы координат линия второго порядка задана общим уравнением Для того чтобы одна из осей имела направление диаметра, сопряженного хордам, параллельным другой оси, необходимо и достаточно, чтобы  , т.е. чтобы уравнение имело вид  Доказательство. Пусть, например, ось   не имеет асимптотического направления. Тогда координаты вектора  параллельного диаметру, сопряженному хордам, параллельным оси  , будут (смотри  ) Но вектор   коллинеарен оси   тогда и только тогда, когда  .  ТЕОРЕМА 16.2. Пусть относительно аффинной системы координат линия второго порядка задана общим уравнением и пусть она имеет единственный центр. Тогда, если оси координат являются сопряженными диаметрами этой линии, а начало координат --- ее центром, то уравнение линии имеет вид где   и  . Обратно, если уравнение линии, имеющей единственный центр, имеет относительно некоторой аффинной системы координат имеет вид где   и  , то начало системы координат является центром линии, а оси координат ее сопряженными диаметрами.  Доказательство. Если оси координат являются сопряженными диаметрами линии, то по теореме 16.1. в ее уравнении отсутствует слагаемое, содержащее произведение  . Так как начало координат является центром, то по теореме 9.1. в ее уравнении отсутствуют   и   в первой степени. Обратно, если уравнение линии второго порядка, заданное относительно аффинной системы координат, имеет вид   то начало координат является центром этой линии по той же теореме 9.1. Поскольку линия имеет единственный центр, координаты которого являются решением системы уравнений  , то 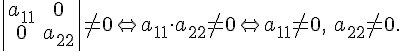 Наконец, так как в уравнении   коэффициент при   равен  , то оси координат являются сопряженными диаметрами этой линии по теореме 16.1. ТЕОРЕМА 16.3. 1. Если аффинная система координат по отношению к эллипсу расположена так, что: a). оси координат являются сопряженными диаметрами эллипса; b). единичной точкой оси   является любая точка пересечения одного из диаметров с эллипсом; c). единичной точкой оси   является любая точка пересечения другого диаметра с эллипсом, --- то уравнение эллипса имеет вид

2. Если аффинная система координат по отношению к гиперболе расположена так, что: a). оси координат являются сопряженными диаметрами гиперболы; b). единичной точкой системы координат является точка пересечения любой из асимптот гиперболы с касательной в любой из точек пересечения одного из диаметров с гиперболой, --- то уравнение гиперболы имеет вид

3. Если аффинная система координат по отношению к параболе расположена так, что: a). осью   является касательная к параболе в любой точке  , лежащей на этой параболе; b). осью   является диаметр параболы, проходящий через точку  ; c). единичная точка системы координат лежит на параболе, --- то уравнение этой параболы имеет вид

Доказательство. 1. Так как оси координат являются сопряженными диаметрами эллипса, то его уравнение по теореме 16.2. имеет вид где   и  . Так как точки   и   принадлежат эллипсу, то справедливы равенства и последнее уравнение принимает вид  или  2. Так как оси координат являются сопряженными диаметрами гиперболы, то ее уравнение по теореме 16.2. имеет вид где   и  . Так как точка   должна лежать на этой гиперболе, а точка   на одной из ее асимптот   то справедливы равенства и последнее уравнение принимает вид  или  3. Диаметр параболы имеет направление, сопряженное по отношению касательной к параболе в той точке, в которой он пересекает параболу, поэтому в общем уравнении параболы по теореме 16.1. должно быть  . Так как, кроме того, начало координат лежит на параболе, то  . Уравнение параболы имеет вид Уравнение касательной к этой параболе в начале координат имеет вид а так как касательной в начале координат по условию является ось  , то это уравнение эквивалентно уравнению  значит, последнее уравнение принимает вид Заметим, что  , так как в противном случае уравнение определяло бы две прямые   и  .  Если бы и  , то линия имела бы единственный центр, а парабола не имеет центров. Значит,  , и уравнение параболы принимает вид Так как единичная точка   лежит на этой параболе, то имеем равенство  , значит,  , и последнее уравнение примет вид  или  ТЕОРЕМА 16.4. Если неособую точку линии второго порядка принять за начало координат, за ось   --- диаметр, проходящий через эту точку, а за ось   --- касательную к линии второго порядка в этой точке, то уравнение линии примет вид где  , и обратно, всякое такое уравнение в случае   является уравнением линии второго порядка, по отношению к которой система координат обладает сформулированными выше свойствами. Доказательство. Так как касательная к линии второго порядка в ее неособой точке имеет направление, которому сопряжен диаметр, проходящий через эту точку, то в общем уравнении линии коэффициент при   равен нулю.  Далее, так как линия проходит через начало координат, то  . Уравнение линии имеет вид Уравнение касательной к этой линии в начале координат имеет вид  и так как касательной в начале координат по условию является ось  , то это уравнение эквивалентно уравнению  значит,   и последнее уравнение принимает вид Обратно, если   то начало координат --- неособая точка линии. Уравнение касательной к этой линии в точке   имеет вид   --- ось  . Диаметр, сопряженный хордам, параллельным вектору  , не имеющему асимптотического направления в силу  , имеет уравнение   --- ось  .