1. Задачи, приводящие к дифференциальным уравнениям.

Решение многих задач естествознания и техники приводит к нахождению неизвестных функций, описывающих рассматриваемые явления и процессы, когда известны соотношения, связывающие между собой эти функции и их производные. Такие соотношения называются дифференциальными уравнениями.

№1. Математическая точка массой m свободно падает под действием силы F_тяж. Найти закон движения точки без учета сопротивления воздуха.

В озьмем ось, направленную вниз. O – начало отсчета. Положение материальной точки определяется на картинке OM=S, изменяющейся в зависимости от времени. F=ma, где F – действующая сила, m – масса, а – ускорение. Так как на тело действует только сила тяжести, то F=mg, а a = , тогда mg = m , следовательно, = g (1)(дифференциальное уравнение).

Искомую функцию S(t) легко получить дважды интегрируя уравнение = g по переменной t: =gt+C₁ (2), S= +C₁t+C₂ (3). Равенство (3) дает решение задачи, т.е. искомый закон движения, но это равенство содержит две постоянные интегрирования. Их можно найти, зная V_{начальн} точки и ее начальное положение.

Пусть |_t=0=V₀ и S|_t=0=S₀ (4), из равенства (2) следует, что C₁=V₀. Из (3) следует, что C₂=S₀. Тогда: S= +V₀t+S₀ (5).

№2. Найти уравнение кривой, зная, что отрезок, отсекаемый касательной в произвольной точке кривой на оси координат, равен удвоенной ординате точки касания.

( ^.)М(х,у) – произвольная точка на прямой.

OB=2y

ОВ=ОК+ВК

ОК=y

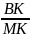=tgß, следовательно, ВК = МК*tgß = х(-у)’ = -ху’

МК=x

y-xy’=2y

xy’+y=0 (6)

xdy+ydx=0 (7), d(xy)=0, xy=C (8), y=C/x (9).

Это семейство кривых (в данном случае гипербол). Для выделения одной из этого семейства нужно задать значение некоторой функции для некоторого значения аргумента.

Для данной задачи, пусть искомая кривая проходит через некоторую конкретную точку M₀ (3,2), тогда, y|_xo=0=2 (10), из (8) следует, что С = 6, тогда y=6/x(11).

2. Основные определения.

Определение: Дифференциальным уравнением называется уравнение, связывающее независимую переменную, неизвестную функцию и ее производные или дифференциалы различных параметров.

F(y⁽ⁿ⁾, y^(n-1), … , y’, y, x) = 0 (12)

y⁽ⁿ⁾=f(x,y,y’,y’’,…,y^(n-1)) (13)

Примеры решения: = g (1), xy’+y=0 (6), xdy+ydx=0 (7),

Во всех этих уравнениях неизвестная функция является функцией одной переменной – такие дифференциальные уравнения называются обыкновенными. Если же неизвестная функция будет зависеть от нескольких переменных, диф.уравнения будут называться уравнениями в частных производных или уравнениями математической физике.

Определение: Порядком дифференциального уравнения называется порядок, входящий в него старшей производной или дифференциала.

Уравнение = g (1) – второго порядка, уравнения xy’+y=0 (6), xdy+ydx=0 (7) – первого.

В некотором случае, когда уравнение является алгебраическим относительно старшей производной, пользуются понятием степени уравнения.

Определение: Степенью дифференциального уравнения называют наибольший показатель степени старшей производной, входящей в это уравнение.

Определение: Любая функция y=f(x), которая удовлетворяет данному дифференциальному уравнении., то есть обращает его в тождество при замене у и ее производных на f(x), называется решение дифференциального уравнения (интегралом).

Примеры:

S= +C₁t+C₂ (3), S= +V₀t+S₀ (5) – решение уравнения = g (1).

y=C/x (9), y=6/x (11) – решение уравнения xy’+y=0 (6) и xdy+ydx=0 (7).