Попытка док-ва Геделя.

1. 0-0

0’-1

0”-2

z

2.П↑ подстановка x на z

X

Применятся, подстановка может только к свободным переменным, а не к связанным.

3.Геделева нумерация

Геделев номер (Г.Н)

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

( ) → ┐ ٧ 0 ' + · = А Р(·) Х В ( ) у

Если взять любую ф-лу состоящую из символов данного алфавита, например:

То для этой ф-лы можно вычислить универсальный Геделев номер.

Существует единственное разложение натурального числа в виде произведения простых чисел с различными степенями.

В любой правильно построенной ф-ле сопоставлено уникальное число, обратное неверно.

Как восстановить ф-лу?

Надо гигантское число разложить на простые множители, затем определить показатели этих сомножителей.

Г(F1,F2…Fm)-это ф-я определяет Г.Н док-во, являющиеся в виде последовательности ф-л F1,F2…

Г(F1,F2…Fm)=

4.Вводится в рассмотрение импликант

1)Д(у,х):=(у=Г(док (х)) – утверждает что «у» - Г.Н док-во ф-л, чей Г.Н – «х».

2)

3)

4) Пусть n0-Г.Н ф-лы G(x)

n0- [G(x)] (4)

G(n0)

Лемма: (G(n0))=S(n0)

Теперь докажем, что G(n0) имеет док-во, то у этого док-ва есть свой Г.Н. Обозначим за m0 Г.Н док-ва.

M0=Г(докG(n0)),получится D(m0, (G(n0))=D(m0,S(n0))= yD(y,S(n0))= ┐ y┐D(y,S(n0))

По ф-ле (3), G(n0)= y┐D(y,S(n0)) (6), ф-ла (5) противоречит ф-ле (6), следовательно нам не удалось док-ть истинности G(n0),

Рассмотрим теперь док-во ложности ф-лы G(n0),

┐G(n0)= ┐ y┐D(y,S(n0))= yD(y,S(n0)) (7)

Попытка найти отрицание ф-лы G(n0) привело к тому, что мы получили док-во S(n0).Если мы проведем это док-во, то получим:

(G(n0))- существование номера Геделевской ф-лы,что противоречит отрицанию.

Теорема Геделя, доказанная в 1931 г. Послужила толчком в области исследования формальной системы. В дальнейшем были сформулированы еще боле сильные ф-лы с простыми док-ми. Было доказано, что множество номеров истинных формул не исчислимо, это нельзя док-ть ни сейчас, ни в каком другом будущем. Все это привело к принципу несовершенства Геделя:

Всякая фундаментальная теория несовершенна - она либо противоречива либо недостаточна для решения всех возникающих проблем.

19. Понятие алгоритма. Свойства алгоритмов. Способы записи алгоритмов.

Алгоритм – (арабского происхождения)предписание, однозначно задающее процесс преобразования исходной информации в виде последовательности элементарных дискретных шагов, приводящих за их конечное число к результату.

Основные свойства алгоритма:

1. Дискретность. Процесс решения протекает в виде последовательности отдельных действий, следующих друг за другом.

2. Элементарность действий. Каждое действие является настолько простым, что оно не допускает возможности неоднозначного толкования.

3. Определенность. Каждое действие определено и после выполнения каждого действия однозначно определяется, какое действие будет выполнено следующим.

4. Конечность. Алгоритм заканчивает работу после конечного числа шагов.

5. Результативность. В момент прекращения работы алгоритма известно, что является результатом.

6. Массовость. Алгоритм описывает некоторое множество процессов, применимых при различных входных данных.

Алгоритм считается правильным, если при любых допустимых данных он заканчивает работу и выдает результат, удовлетворяющий требованиям задачи. Алгоритм однозначен, если при применении к одним и тем же входным данным он дает один и тот же результат.

Схема определения алгоритма в практическом смысле выглядит так:

1. Всякий алгоритм применяется к исходным данным и выдает результирующие данные. В ходе работы алгоритма появляются промежуточные данные. Для описания данных фиксируется набор элементарных символов (алфавит данных) и даются правила построения сложных данных из простых. Примеры простых данных: целые и действительные числа, логические переменные, символьные переменные. Примеры сложных данных: массивы, строки, структуры.

2. Данные для своего размещения требуют памяти. В ЭВМ память состоит из ячеек. Единицы объема данных и памяти согласованы, и в прикладных алгоритмических моделях объем данных можно измерять числом ячеек, в которых данные размещены.

3. Элементарные шаги алгоритма состоят из базовых действий, число которых конечно. Под ними можно подразумевать машинные команды, входящие в набор команд ЭВМ. При записи алгоритмов на языках высокого уровня в качестве базовых действий могут выступать операторы языка.

Можно выделить три крупных класса алгоритма:

вычислительные, информационные и управляющие.

Вычислительные алгоритмы, как правило, работают с простыми видами данных (числа, матрицы), но сам процесс вычисления может быть долгим и сложным.

Информационные алгоритмы представляют собой набор сравнительно небольших процедур

(например, поиск числа, слова), но работающих с большими объемами информации (базы данных). Для того чтобы они работали эффективно, важно иметь хорошую организацию данных.

Управляющие алгоритмы характерны тем, что данные к ним поступают от внешних процессов, которыми они управляют. Результатом работы этих алгоритмов являются различные управляющие воздействия.

Способы записи алгоритмов:

1.словесный (“-“плохо формализует)

2.схематичиский

3.псевдоязыки

При записи алгоритма необходимо неукоснительно соблюдать 3 свойство. Понятие элементарности может меняться в зависимости от исполнителя – это человек или механическое устройство выполняющее алгоритм.

20. Понятие алгоритмической системы. Понятие вычислимости.

Понятие алгорифмической системы – это набор типов исходных и результирующих объектов, а также методов их исследования, их обработки, описываемых на понятном для устройства языках

Алгоритм с т.з алгорифмической системы – это система вычисления, которая для некоторого класса задач А при помощи одинаковой определённой операции совершаемых механизмами (без участия человека) получить запись В, т.е решение задач.

Алгоритм – это процедура, которая применяется к определённым входным данным.

Алгоритм разбит на шаги:

S*= Ω (S)

Преобразование происходит однозначно заданным способом, процесс преобразования происходит до тех пор пока произойдет без результативная остановка или у оператора возникнет неопределенное состояние, либо появится сигнал о полученном решении.

А0=А : А1= Ω(А0) : А2= Ω(А1):

Аn= Ω(Аn-1): В=Ак

Применение алгоритма к некоторым исходным данным:

Любой алгоритм над которым необходимо произвести действие может быть представлено натуральным числом. В результате применения алгоритма также должно получится натуральное число, либо не получится в случаи ошибки. Процесс обработки любой информации может быть назван, а для кого-то сведен к вычислению алгоритма и вычисления тесно связаны между собой.

Понятие вычисляемости.

вычисление≡преобразование

Выполнение алгоритма аналогично вычислению функции y=f(x) ,y=f(x1,x2,…xn)

f:Х→У

f-некоторое отношение, которое хĘХ ставим в соответствие уĘУ, всюду определенная функция у=к+1 частичная функция у=1/х.

Назовем m-местную ф-ю fвычислимой, если существует алгоритм её вычисления А, такой что выполняется 2 условия:

1.При подаче на его вход вектора

х=<x1,x2,…xm>принадлежит общее определение функции Дf. Алгоритм, через конечное число шагов останавливается и выдает результат f(x).

2. Если вектор х не принадлежит Дf алгоритм иногда не останавливается.

21. Частично-рекурсивные функции. Тезис Черча.

(Гедель, Клини 1936)

Базис:

0(Х)=1

S(x)=x+1

m

I (x1,x2,…xm)= функция проекции.

n

Механизмы.

1.Суперпозиция

F(x)= (g1,(x),g2(x),…gk(x)).

2.примитивная рекурсивная

n≥0 из n-местной функции fk (n+2)- местной функции n(n+2)….(n+1) местная функция n(n+1)

n(x,0)=f(x)

n(x,y+1)=g(x,y,n(x,g))

n=0

n(0)=a, a=const

n(y+1)=g(y,h,(y))

функция полученная с помощью суперпозиции к примитивно рекурсивной будем называть примитивнорекурсивными.

Пример

1. sum(x,y)=x+y

sum(x,0)=x=x(x,0)

sum(x,y+1)=x+(y+1)=(x+y)+1=sum(x,y)+1=S(sum(x,y))

2. умножение

mul(x,y)=xy

mul(x,0)=0=0(x)

mul(x,y+1)=x(y+1)=xy+x=sum(mul(x,y);x)

3.fact(0)=1

.fact(y+1)=mul(fact(y);sum(y,1))

4.усеченное вычитание

S(x){x-1,x>0

0,x=0

S(0)=0=0(x)

S(y+1)=y=I(x,y)

4.оператор минимизации

Ставим в соответствии ф-и f ф-ю

m+1 m

F:N →N h:N →N

1.Dn={x,xm+1≥0,f(x,xm+1)=0

<x,y> Df для y≤xm+1}

2.h(x)=min y, f(x,y)=0

h(x)=m(f(x,y)=0

алгоритм вычисления h стоит в подчинении значения f(x,y) последовательно у=0,1,1,2… при которых найдется у обращающий функцию.

Все функции которые можно получить из базы только этими 3 способами, будет называться частично рекурсивными. Если ф-я всюду определена, то она называется общерекурсивной.

Тезис Герча:

Класс машинно- вычислительных частичных ф-й совпадает с классом всех частично вычислительных ф-й

22. Сложность алгоритма. Оценки сложности алгоритмов. Классификация алгоритмов по сложности.

Оценка сложности алгоритма

Сложность алгоритма помогает оценить затраты на его реализацию и определяется вычислительными мощностями, необходимыми для его выполнения. Она часто измеряется двумя параметрами: T(временная сложность) и S (пространственная сложность, или требования к памяти). И T и S обычно представляются в виде функций от n, где n - размер входных данных.

Пусть А - алгоритм для решения некоторого класса задач, а n - размерность отдельной задачи из этого класса. В общем случае n может быть длиной обрабатываемой последовательности данных. Определим f(n) как рабочую функцию, дающую верхнюю границу для максимального числа основных операций (сложения, сравнения и т.д.), которые должен выполнить алгоритм.

Определим асимптотическую сложность алгоритма А. Если алгоритм обрабатывает входную последовательность (ВХП) размера n за время cn², то говорят, что временная сложность этого алгоритма - Q(n²) (читается: порядка n²). Точный смысл этого утверждения такой: найдутся такие константы c1, c2 > 0 и такое число n0, что c₁n² ≤ f(n) ≤ c₂n² при всех n ≥ n₀. Вообще, если g(n) - некоторая функция, то запись f(n) = Q(g(n)) означает, что найдутся такие c1, c2 > 0 и такое n₀, что c₁g(n) ≤ f(n) ≤ c₂g(n) при всех n ≥ n₀.

Запись f(n) = Q(g(n)) включает в себя две оценки - верхнюю и нижнюю. Их можно разделить (в данном случае нас больше интересует верхняя оценка). Говорят, что f(n) = O(g(n)), если найдется такая константа > 0 и такое число n₀, что 0 ≤ f(n) ≤ cg(n) для всех n ≥ n₀. Также существуют определения:

Функция f(n) является O[g(n)] (о-большое) для больших n, если:

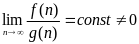
Функция f(n) является o[g(n)] (о-малое) для больших n, если:

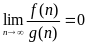
Говорят, что алгоритм А - полиномиальный, если f(n) растет не быстрее, чем полином от n. При этом в качестве g(n) оставляют член, быстрее всего растущий при увеличении n. При этом все члены низших порядков игнорируются.

Пример: Если временная сложность алгоритма описывается как T(n) = 4n² + 7n + 12, то вычислительная сложность определяется, как O(n²).

Временная сложность, определяемая таким образом не зависит от реализации. Не нужно знать ни точное время выполнения различных инструкций, ни число битов, используемых для представления различных переменных, ни даже скорость процессора. Один компьютер может быть на 50 процентов быстрее другого, у третьего шина данных может быть в два раза быстрее, но сложность алгоритма, оцененная по порядку величины, не изменится. Запись оценки сложности позволяет увидеть, как объем входных данных влияет на требования ко времени выполнения. Например, если T(n) = O(n), то удвоение входных данных удвоит и время работы алгоритма. Если T = O(2ⁿ), то добавление одного бита к входным данным удвоит время выполнения.