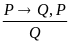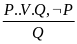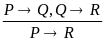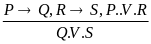2.2. Пропозициональные формулы

Символы ך,&,V,→,≡ называются пропозициональными связками. Латинскими заглавными буквами будем обозначать пропозициональные буквы, или высказывания. Тогда:

1. Все пропозициональные буквы есть пропозициональные формулы (ПФ).

2. Если А и В - пропозициональные формулы, то (ך), (A & B), (A V B), (А → B), (А ≡ B) – тоже пропозициональные формулы.

3. Только те выражения являются пропозициональными формулами, для которых это следует из п.1 и п.2.

Всякая ПФ определяет некоторую истинностную функцию, которую можно представить истинностной таблицей, которая устанавливает соответствие между всеми возможными наборами переменных, входящих в формулу и значениями формулы. Таблицы истинности применяются для:

• вычисления истинности сложных высказываний;

• установления эквивалентности высказываний;

• определения тавтологий. Рассмотрим ПФ и построим для нее ИТ.

((A ≡ B ) → (( ך A) & B))

И И И Л Л И Л И

Л Л И И И Л И И

И Л Л И Л И Л Л

Л И Л Л И Л Л Л

Удаление и восстановление скобок в ПФ

При возрастании сложности формулы, количество скобок становится большим и затрудняет восприятие. Поэтому используют сокращенную, в которой расположение скобок можно восстановить в любое время.

При удалении скобок придерживаются следующих правил:

1. У формул опускается внешняя пара скобок, то есть ((AVB)&(ךC)) превращается в (AVB)&(ךC)

2. Если формула содержит вхождение только одной бинарной связки (→,V,&,≡), то для каждого вхождения этой связки опускаются внешние скобки у той из двух формул, соединяемых этим вхождением, которая стоит слева. Например, формула (((A → B) → C) → D) может быть записана в виде A → B → C → D.

3. Связки считают упорядоченными следующим образом: ≡,ё→,V,&,ך и опускают все те пары скобок, без которых невозможно восстановление формулы на основе следующего правила. Каждое вхождение знака ך относится к наименьшей подформуле, следующей за ним; после расстановки всех скобок, относящихся ко всем вхождениям знака ך , каждое вхождение знака & связывает наименьшие формулы, окружающие это вхождение; затем, каждое вхождение знака V связывает наименьшие формулы, окружающие это вхождение; и, подобным образом для → и ≡. При применении этого правила к одной и той же связке мы продвигаемся слева направо.

Рассмотрим примеры.

В формуле A V ךB → C ≡ A скобки восстанавливаются в следующей последовательности:

1. A V (ךB) → C → A

2. (A V (ךB)) → C → A

3. ((A V (ךB)) →C) → A

4. (((A V (ךB)) → C) → A)

Для формулы D →C →A&D&B V ךD → B последовательность восстановления скобок будет следующая:

1. D → C →A&D&B V(ךD) →B

2. D →C → (A&D)&B V(ךD) → B

3. D → C → ((A&D)&B)V(ךD) → B

4. D →C → (((A&D)&B)V(ךD)) → B

5. D →C → ((((A&D)&B)V(ךD)) → B)

6. (D → C) → ((((A&D)&B)V(ךD)) → B)

7. ((D → C) → ((((A&D)&B)V(ךD)) → B))

8. Интерпретация, тавтология, противоречие. Логическое следование и логическая

эквивалентность.

Определение. Каждому атому, входящему в формулу, можно приписать значение истина или ложь. Каждая возможная комбинация таких значений, приписанных атомам формулы, называется интерпретацией. Формула может быть истинной при одной интерпретации и ложной при другой. Значение формулы А в интерпретации I будем обозначать I(A). Формула, истинная при некоторой интерпретации, называется выполнимой. Формула, истинная при всех возможных интерпретациях, называется общезначимой (тавтологией). Формула, ложная при всех возможных интерпретациях, называется невыполнимой, или противоречием.

Пример тавтологии: (AV(ךA))

Доказательство легко проводится построением ИТ.

Доказать тавтологию: (A & B) → (A V B)

Для доказательства строим ИТ: ( A & B ) → ( A V B )

И И И И И И И

И Л Л И И И Л

Л Л И И Л И И

Л Л Л И Л Л Л

Пример противоречий: (A ≡ ( ךA )), (A & ( ךA ))

Следование и эквивалентность

Формулы А и В являются логически эквивалентными, если при любых значениях переменных, входящих в эти формулы значение А совпадает со значением В. Если A и В - эквивалентны, то (A ≡ B) - тавтология. Логически эквивалентные формулы будем обозначать знаком ”=”. Если (A → B) является тавтологией, то говорят, что A логически влечет B, или В является логическим следствием А. Логические следование и эквивалентность играют исключительно важную роль в математической логике, позволяя проводить преобразования пропозициональных формул и решать логические задачи.

Теорема Имеет место следующая логическая эквивалентность: (A→ B) = (ךAVB)

Доказательство. Для доказательство достаточно проверить, что формулы действительно имеют одинаковые значения при всех интерпретациях.

( A → B ) = (( ך A) V B)

И И И Л И И И

И Л Л Л И Л Л

Л И И И Л И И

Л И Л И Л И Л

Утверждение “Если P, то Q, иначе R” широко используется в программировании может быть представлено формулой (P → Q)&(ךP →R). Ей соответствует фраза: “Если Р, то Q, а если не P, то R”.

Логическая формула, представляющая приведенное выше высказывание имеет вид:A → (ךB) Существует множество формул, эквивалентных данной. Интерпретируя эти формулы в естественном языке, получим следующие утверждения, которые все эквивалентны между собой:

A → ךB Порядочный человек не может быть вором

ךAV ךB Или он не порядочный человек, или он не вор

ך(A&B) Порядочность и воровство несовместимы

B → ךA Если человек вор, то он не является порядочным человеком

Примеры логически эквивалентных формул

Рассмотрим наиболее важные эквивалентные формулы, часто используемые при анализе рассуждений и написании программ.

1. Отрицание дизъюнкции эквивалентно конъюнкции отрицаний (1-й закон де Моргана): ך(AVB) = (ךA)&(ךB)

2. Отрицание конъюнкции эквивалентно дизъюнкции отрицаний (2-й закон де Моргана): ך(A&B) = (ךA)V(ךB)

3. Импликация эквивалентна импликации отрицаний (контрпозиции): (A → B) = (ךA) → (ךB)

4. Конъюнкция и импликация: (A&B) = ך(A → (ךB))

5. Конъюнкция и дизъюнкция: (A&B) = ך(ךA V ךB)

Примеры использования законов де Моргана

Пример 1. Утверждение “Симпсон будет признан судом виновным тогда и только тогда, когда все 12 присяжных заседателей признают его виновным” может быть записано в виде формулы B≡(A1&A2&...&A12), где B означает виновность, а An - факт признания вины n-ым присяжным заседателем. Равносильная ей формула ךB≡ ך(A1&A2...&A12) по закону де Моргана может быть преобразована в формулу ךB≡(ךA1 V ךA2 &...ךA12), которую можно интерпретировать так: “Симпсон не будет признан судом виновным тогда и только тогда, когда хотя бы один из 12 присяжных заседателем не признает его вины”.

Пример 2. Рассмотрим следующую задачу. Имеется текстовый файл, который необходимо прочитать посимвольно до появления любого из трех символов: (%,#,EOF). Привести возможные варианты решения этой задачи. В первую очередь нас интересует построение условия для циклической конструкции, выполняющей чтение символов из файла. Обозначим факт появления первого символа как А, второго - как В и третьего - как С. Тогда условие, при котором читаются символы из файла будет записано в виде следующей формулы: (ךA)&(ךB)&(ךC) Однако для данной формулы имеется логически эквивалентная ей конструкция: ך(A V B V C) Поэтому можно предложить два варианта реализации цикла чтения содержимого файла на языке программирования С.

9. Законы логики.

Равносильности формул логики высказываний часто называют законами логики. Знание законов логики позволяет проверять правильность рассуждений и доказательств.

Закон тождества. Он сформулирован древнегреческим философом Аристотелем. Закон тождества утверждает, что мысль, заключенная в некотором высказывании, остается неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует. (A = A)

Закон противоречия говорит о том, что никакое предложение не может быть истинно одновременно со своим отрицанием. (A&(ךA)) = ”Это яблоко спелое” и ”Это яблоко не спелое”.

Закон исключенного третьего говорит о том, что для каждого высказывания имеются лишь две возможности: это высказывание либо истинно либо ложно. Третьего не дано. ”Сегодня я получу 5 либо не получу”. Истинно либо суждение, либо его отрицание. (AV(ךA)) =

Закон двойного отрицания. Отрицать отрицание какого-нибудь высказывания - то же, что утверждать это высказывание. ”Неверно, что 2x2 не равно 4” . (ך(ךA)) = A

Законы идемпотентности. В алгебре логики нет показателей степеней и коэффициентов. Конъюнкция одинаковых ”сомножителей” равносильна одному из них. (A&A) = A, (AVA) = A

Законы коммутативности и ассоциативности. Конъюнкция и дизъюнкция аналогичны одноименным знакам умножения и сложения чисел.

Коммутативность: (A&B) = (B&A), (AVB) = (B VA)

Ассоциативность: (A&B)&C = A&(B&C) (AVB)VC = AV(B VC)

Законы дистрибутивности. В отличие от сложения и умножения чисел логическое сложение и умножение равноправны по отношению к дистрибутивности: не только конъюнкция дистрибутивна относительно дизъюнкции, но и дизъюнкция дистрибутивна относительно конъюнкции:

A&(B VC) = (A&B)V(A&C); AV(B&C) = (AVB)&(AVC)

Законы де Моргана: (ך(A&B)) = ((ךA)V(ךB)) - отрицание логического произведения эквивалентно логической сумме отрицаний множителей; (ך(AVB)) = ((ךA)&(ךB)) - отрицание логической суммы эквивалентно логическому произведению отрицаний слагаемых.

Законы поглощения A&(A V B) = A; AV(A&B) = A

Законы склеивания (AVB)&((ךA)VB) = B; (A&B)V((ךA)&B) = B

10. Понятие теоремы. Основная теорема логического вывода и ее доказательство.

• Формула G теории L называется теоремой теории L, если существует вывод в L, в котором последней формулой является G. Вообще говоря, может не существовать алгоритма, позволяющего по формуле определить существование ее вывода. Теория, для которой такой алгоритм существует, называется разрешимой, в противном случае – неразрешимой.

Доказать теорему означает построить вывод в данной Формальной Теории.

• Лемма: формула, которая используется в процессе вывода и сама имеет вывод в данной формальной теории.

Построение вывода для заданной формулы является непростой задачей. Ещё более сложной задачей может быть ответ на вопрос: А существует ли данный вывод?

Одной из важнейших задач современной науки является:

1. Построение алгоритмов, определяющих существует доказательство алгоритмов или нет. Если такой алгоритм удается построить для теории, то теория называется разрешимой.

2. Построение методов алгоритмического доказательства теоремы.

Основная теорема логического вывода

Теорема. Формула G является логическим следствием формул F1, F2, . . . Fn тогда и только тогда, когда формула F1&F2&. . .&Fn → G является тавтологией.

(А≡В)=(А→В)&(В→А)Для доказательства теоремы необходимо доказать необходимость и достаточность

Доказательство.

Лемма 1. Если формула А→В является тавтологией, то В принимает истинное значение при тех интерпретациях при которых истина А.

А→В

Предположим, что В принимает такое значение при той интерпретации при которой истинно А. Но тогда функция будет принимать каждое значение, что противоречит условию, т. е. А – истина и В – истина.

Согласно Лемме1 можно сформулировать другое определение логического следствия, а именно:

Формула В является логическим следствием формулы А, если она истина при тех интерпретациях при которых истина А.

G (F₁, F₂,…Fn)

(F1&F2&. . .&Fn) → G (*)

F1&F2&. . .&Fn (**)

Докажем необходимость

Предположим чтоG является логическим следствием F₁, F₂,…Fn . Требуется доказать что (*) – тавтология.

Пусть I – произвольная интерпретация.

Если все формулы F₁, F₂,…Fn истина на I

I(f1)=I(F2)=….I(Fn)=И и по определению логического следствия I(G)=И, то формула (*) – истина.

Если хотя бы одна из F принимает значение Л, то (*) все равно Истина(т.к. Л→И). Следовательно формула (*) - тавтология.

Докажем достаточность.

Предположим, что (*) - тавтология. Надо доказать что G является логическим следствием.

Для всякой интерпретации I, на которой все Fi истинны, формула (**) тоже истинна, и поскольку (*) - тавтология, G - тоже истинна. .

Теорема Формула G является логическим следствием формул F1, F2, . . . Fn тогда и только тогда, когда формула F1&F2&. . .&Fn→ ךG является противоречием.

11. Силлогизмы с точки зрения формальной теории.

Силлогизмы, которые мы рассматривали на первой лекции, не имели формального описания и целиком определялись естественным языком. Сейчас мы запишем основные виды силлогизмов формально с указанием их названий в современной логике. Отметим также, что все приведенные в следующей таблице схемы рассуждений являются правильными и их можно использовать для доказательств без дополнительных обоснований.

Схема силлогизма	Название	Пример
	modus ponens (правило спуска)	Если идет дождь, то на небе туча. Идет дождь, следователь на небе туча.
	доказательство от противного	Если заболел, то чихаю. Не чихаю, следовательно не болею.
	дизъюнктивный силлогизм	Мальчик или девочка. Не мальчик, следовательно девочка.
	гипотетический силлогизм	Если заболел, то чихнул. Если чихнул, то заразил, следовательно если заболел, то заразил.
	простая конструктивная дилемма	Если проспал, то опоздал, если не доехал, то опоздал. Если и то и то, то опоздал.
	сложная конструктивная дилемма
	простая деструктивная дилемма
	сложная деструктивная дилемма

12. Формальная теория для исчисления высказываний.

Дадим определение такой теории:

1. Алфавит: Ā={┐, → , ( , ) , A, B…..}

2. Формулы:

• A,B,C - все пропозициональные буквы суть формулы;

• если А и В - формулы, то (ךA), (A→B) - тоже формулы.

3. Схемы аксиом:

B1: (A→ (B→ A)) → (А→В) → (А→С))

B2: (A→ (B → C))

B3: ((┐B → ┐A) → (┐B→A) → B))

4. Правила вывода:

Modus ponens:

R1:

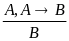
R2: ∏^Q_p F (p) =F (Q)

5. Подстановка: из формулы F(A), содержащей букву А выводима другая формула F(G), полученная заменой А на G. Другие связки вводятся с помощью определений:

A&B = ┐(A→┐B)

AVB=┐A→B

А≡В=(А→В)&(В→А)

Докажем вывод в предложенной теории формулы A→A

1.Подставляем А вместо С в аксиому B1.

F1: (A→ (B→A)) → ((A→B) → (A→A))

2. Используем правило R1: в качестве первой посылки берем F1, а в качестве второй - аксиому (В1):

F2: (A → B) → (A → A)

3. В формулу F2 вместо В подставляем B → A:

F3: (A→ (B→ A)) → (A →A)

4. Используем R1: первая посылка - формула F3, вторая – аксиома (В2).

F4: A→A.

Свойства:

1) Все теоремы Исчисления Высказывания являются тавтологиями ׀=F

2) Исчисления Высказывания является полной теорией если в ней можно повторить либо формулу F либо ┐F

3) Исчисления Высказывания непротиворечивая теория если в ней недоказуемая формула F&┐F

13. Метод резолюций в логике высказываний.

Метод резолюций используется для проверки того факта, что F является тавтологией. Метод резолюций позволяет рассмотреть формулу ┐F и доказать, что это противоречие формула.

Описание метода:

Для того, чтобы доказать, что формула F является тавтологией, необходимо рассмотреть формулу ┐F и доказать, что это противоречие формула.

┐F приводится к конъюнктивной нормальной форме, которая представляет собой формулу, записанную в виде конъюнкций элементарных дизъюнкций: ┐F=D₁&D₂&Dn, таким образом, формируется множество дизъюнкций. Di,j – этого множества, содержащее переменную и её отрицание формируют треть D – РЕЗОЛЬВЕНТА.

Di=Di V Y

Dj=Dj V ┐Y

Di V Dj = Di’ V Dj’

Если Di = Y, Dj = ┐Y

Di V Dj = 

Неоднократно применяя правило резолюции к множеству дизъюнкций стремятся получить пустую резольвенту, что говорит о противоречии ┐F следовательно о тавтологии F. Если пустую резольвенту получить не удалось, то рассуждение не корректно.

Задача

В исходных формулах избавляемся от всех операций кроме отрицания и дизъюнкций.

(P →Q) = (┐P V Q)

F1: ┐(┐A) V ┐B = A V ┐B

F2: ┐(┐C) V ┐A = C V ┐A

F3: B

G: ┐C

Заменяем G на её отрицание. Получаем множество дизъюнкций

{ (A V ┐B) , (C V ┐A) , B, ┐C }

D₁ D₂ D₃ D₄

Образуем резольвенты

D₅ = D₁ V D₂ = A V ┐B V C V ┐A = (┐B V C)

D₆ = D₄ V D₅ = ┐B V C V ┐C = ┐B

D₇ = D₆ V D₃ = ┐B V B = 

Задача

В хоккей играют настоящие мужчины, трус не играет в хоккей, я не играю в хоккей, значит я трус.

Х – я играю в хоккей

М - я мужчина

F1: М V ┐X , X→M

F2: M V ┐X

F3: ┐X

G: ┐M

Если взять ┐ => (M), то получим множество дизъюнкций, из которых не возможно получить ни одной резольвенты, значит высказывание некорректно.

14. Синтаксис и семантика языка логики предикатов. Формулы логики предикатов.

Логика предикатов – это высказывание, зависящее от параметров. Таким образом, предикат - это высказывание-функция, значение (истина/ложь) которого зависит от параметров.

х >2 Р(х)= {^И_Л

х > y ; P(2,6)= Л

P(6,0)= И

Предикатная форма может строится из следующих элементов:

1. х, у, ….. – переменные

2. Р( ), Q( ) – предикаты

3. А, В, … - константы

4. ┐, &, V, →, ≡ логические связи

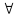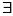5. , - кванты (существование и т. д.)

Формулы

Правильно построенные формулы логики предикатов - это комбинации атомных предикатов и констант с логическими связками. Они определяются рекурсивно над множеством атомных предикатов с помощью связок ך,→, скобок и одной дополнительной связки

формулы:

1. Атомные предикат есть формула.

2. Если Р - формула, то ך(P) - тоже формула.

3. Если Р, Q - формулы, то (P→ Q) - тоже формула.

4. Если Р - формула, то ( x)P - тоже формула.

5. Никаких других формул нет.

В логике предикатов для сокращения формул используются записи:

• P V Q для (ךP) → Q,

• P&Q для ך(P →ךQ),

• P→ Q для (P → Q)&(Q → P),

• ( x)P для ך(( x)ךP).

Связки , называются кванторами. Присоединение квантора с переменной к предикатной формуле называется навешивание квантора на переменную х. Переменная при этом называется связанной и вместо нее подставлять константы уже нельзя.

Например, Афоризм Козьмы Пруткова “Нет столь великой вещи, которую не превзошла бы величиной еще большая“ формально может быть записан так: ך( xך y P(y, x)), где x y принимают значения на множестве всех вещей. Этот предикат имеет эквивалент: ( x yP(y, x)), что дает эквивалентную формулировку афоризма: “Для любой вещи всегда найдется еще большая“.

тся теорией первого порядка, в которой кванторы навешиваются на предметные переменные.

Формальные теории первого порядка представляют собой яркий пример формальных теорий с аксиоматикой и правилами вывода и обладают следующим свойством: в них кванторы могут связывать только предметные константы, а не предикаты. Будем рассматривать теорию, в которой используются две логические связки ( ך,→) и кванторные символы ( , ). Множество аксиом представлено следующими схемами:

A1. A → (A → B),

A2. (A → (B → C)) → ((A → B) → (A → C)),

A3. (ךA → ךB) → (B → A),

A4. x F(x) → F(y),

A5. F(y) → x F(x).

В любой теории первого порядка имеются следующие правила вывода:

A, A → B (R1) B → A(x) (R2) A(x) → B (R3)

B B → x A(x) x A(x) →B

Покажем на примере, как с помощью нашей теории доказывается знаменитый аристотелевский силлогизм:

Все люди смертны. Сократ - человек. Следовательно, Сократ смертен.

Все, кто обладает свойством P, обладает свойством Q. y обладает свойством P. Следовательно, y обладает свойством Q.

Обосновать силлогизм на языке предикатов - это значит записать его три утверждения на этом языке и показать, что из посылок (первых двух утверждений) выводимо заключение (третье утверждение).

P( ) – быть человеком

Q( ) – быть смертным

x(P(x) → Q(x))

P(y) .

Q(y)

Формальный вывод заключения из посылок состоит в следующем:

1. В первую аксиому A₄ вместо F(x) подставим P(x) →Q(x). Получим: x(P(x) →Q(x)) → (P(y) →Q(y)).

2. Из предыдущей формулы и первой посылки по правилу заключения R₁ следует, что формула:

P(y) →Q(y).

3. Из предыдущей формулы и второй посылки по правилу заключения R1 выводима формула Q(y), ч.т.д.

Ограниченные предикаты

( x є Х)P(x) (1)

( x є Х )P(x) (2)

Как и в логике высказываний, в логике предикатов имеются эквивалентные соотношения, позволяющие преобразовывать предикатные формулы.

Эквиваленты

x [ (x є Х) →P(x) ] (1)

x [ (x є Х )& P(x) ] (2)

( x: R(x)) P(x) если выполняется R(x), то выполняется Р(х)

( x: R(x))P(x)

Эквиваленты

x [R(x) →P(x) ]

x [R(x)& P(x) ]

Для ограниченных предикатов выполняются законы Де Моргана, связанные с внесением отрицания под квантор.

ך( x :R(x)) P(x)= ( x: R(x))ךP(x)

ך( x: R(x)) P(x) = ( x: R(x))ךP(x)

Пример:

Кто не рискует, тот не пьет шампанское

Q(x) – пить шампанское

P(x) – рисковать

x(┐P(x) → ┐Q(x)) Эквивалент: ( x: ┐P(x)) ┐Q(x); ┐( x: ┐P(x) Q(x)

Понятие терма.

Множество объектов, о которых даются утверждения, называется предметной областью, а сами отношения между n объектами - n-местными предикатами. С математической точки зрения n-местный предикат - это функция P(x₁, . . . , xn) от n переменных, причем переменные принимают значения из предметной области, а функция P принимает два значения .

Нечетность - одноместный предикат. Если его обозначить через P1(x).

• n-местным предикатом P(x₁, x₂, ..x_n) называется функция P: Mⁿ → {True, False}, определенная на наборах длины n элементов некоторого множества M и принимающая значения в области True, False. Множество М называется предметной областью предиката, а x₁, x₂, ..xn - предметными переменными.

• Термом будем называть переменную или константу предметной области М или функцию, принимающую значения в предметной области. Пусть t₁, t₂, ..t_n- термы. Атомный предикат - это n-местная функция F(t1, t2, ..tn), принимающая значение на множестве И,Л.

15. Формальная арифметика. Непротиворечивость формальной арифметики. Теорема

Генцена.

Формальная арифметика – это теория, в которой имеются следующие объекты:

1) Предметы констант: 0

2) Три функтора:

Двухместные + •

Одноместные ‘

3) Двухместная предиката =

4) термы t₁, t₂…….

5) предикаты Р( ), Q( ) …

В формальной арифметики определены следующие аксиомы:

(P(o)& x(P(x) → P(x’))) → x P(x)

t₁’=t₂’ → t₁=t₂

┐(t₁’=0)

t₁=t₂→ (t₁=t₃→t₂=t₃)

t₁=t₂→t₁’=t₂’

t₁+0=t₁

t₁+t₂’= (t₁+t₂)’ t₁=5 t₂’=7 5+7=(5+6)’

t•0=0

t₁•t₂’=t₁•t₂+t₁

Непротиворечивость формальной арифметики.

Метод математической индукции входящей в качестве аксиомы в формальную арифметику может быть расширен за счет применения его к множеству трансфинитных чисел.

Финитные числа – это натуральные, трансфинитные идут за натуральными.

Теорема Генцена 1936

Непротиворечивость формальной арифметики доказывается в более широкой формальной теории, содержащей арифметику и принцип трансфинитной индукции.

16. Неклассические логики: модальная, темпоральная, нечеткая.

Нечеткая логика допускает континуальное число истинностных значений для высказываний. В простейшем случае эти значения принадлежат отрезку [0,1] действительных чисел. Иначе говоря между значением 0, соответствующим классическому _┴ (ложь) и 1, или ┬ (истина), имеем несчетное число промежуточных истинностных значений α є (0,1).

Нечеткая логика широко используется в современной прикладной математике и технических науках.

Пусть Е некоторое фиксированное множество и М=[0,1] – отрезок действительных чисел.

Нечеткое подмножество А множества Е – это множество пар вида

{(x, μ_А(x)): x €E}, где μ_А : Е→М – функция.

Множество нечетких множеств не является булевой алгеброй, следовательно логика построенная на нечетких множествах будет неклассической.

Модальная логика

Модальная логика строится на основе логики высказываний за счет добавления новых законов, позволяющих выражать отношение тех или иных высказываний к окружающей действительности. Как правило, это суждение о возможности или необходимости чего-либо.

Различают три типа модальностей, каждый из которых подразделяется на виды:

• Алетические модальности. Это высказывания, содержащие такие виды модальности, как «необходимо», «возможно», «невозможно», «случайно».

• Деонтические модальности. Это модальности с характеристиками действий и поступками людей в обществе. Например, «обязательно», «разрешено», «запрещено», «безразлично».

• Эпистемические модальности. Характеристики наших знаний. Можно назвать такие виды модальности этого типа, как «доказано», «опровергнуто», «не доказано», «не опровергнуто», «знает», «верит», «убежден», «сомневается».

Темпоральная (временная) логика – это модальные логики. Они строятся добавлением к логике высказываний новых знаков, отражающих свойства времени. Например процесс выпадения дождя. Это процесс продолжается некоторое время, а затем прекращается. Но предположим, что это происходит не внезапно, а постепенно. Пусть А……….┐А, иллюстрирует что на определенном отрезке времени вначале определенно идет дождь(А), потом определенно не идет дождь (┐А), а между этими временными точками находится переходная область, когда, капает небольшое количество капель. В этой области А ни истинно, ни ложно. Т. о., появляется еще третье значение высказывания: «ни истинно, ни ложно»; или «и истинно, и ложно»; или «неопределенность».

17. Логическое программирование.

Как решать задачи на ЭВМ. Математик разрабатывает алгоритм решения задачи, а программист, используя один из языков программирования, реализует предложенный алгоритм в виде программы.

Или иной подход: задачу надо представить в виде высказывания, доказательство которого следует предоставить ЭВМ.

Таким образом компьютеру предоставляется не алгоритм, а описание предметной области задачи и сама задача в виде формул формального исчисления. Решение задачи является в таком случае выводом в данном исчислении. От программиста требуется описать с достаточной степенью полноты предметную область и формулировку задачи на языке этого исчисления, а поиск вывода, приводящего к решению задачи, поручается компьютеру.

Логическая программа представляет собой конечный набор формул логики предикатов одного из следующих выводов:

P (t₁,t₂…..tn).

Q(s₁,…, s_k): - Q₁(s₁,…, s_k),…, Qm(s₁,…..s_k).

Где Q1,Q2,…Qm – предикаты, а t₁,…,tn, s₁,…, s_k – термы. Формулы первого вида называются фактами, второго – правилами. Факт - один единственный экземпляр, свойство или отношение между объектами.

Правило читается как «Q(s₁,…, s_k) истинно, если истины Q₁(s₁,…, s_k),…, Qm(s₁,…..s_k) ». Формула Q(s₁,…, s_k) называется ЗАГОЛОВКОМ правила. Правило позволяет выводить новые факты из уже имеющихся.

Таким образом, логическая программа состоит из конечного числа фактов и правил. В фактах и правилах описывается логическая модель предметной области.

Логическая программа задает множество следствий, которые являются результатом программы. Выполнение логической программы – это вывод следствия из него.

Логическое программирование предполагает наличие логической машины, называемой интерпретатором, который осуществляет процесс логического вывода.

Для реализации идей логического программирования разработаны различные языки логического программирования, такие как PROLOG, TURBO PROLOG и т. д.

18. Теорема Геделя о неполноте и суть ее доказательства.

Во всякой теореме 1-го порядка, включающей формальную арифметику:

1.сущ-ет истинная ф-ла А, истинность которой нельзя ни док-ть, ни опровергнуть.

2. утверждение о непротиворечивости данной теории- это ф-ла данной теории, которую нельзя док-ть.