27. Дайте определение выпуклого множества в Rn. Приведите примеры выпуклых множеств в r2, объединение которых: а) является выпуклым множеством; б) не является выпуклым множеством.

Ответ: Множество называется выпуклым, если оно содержит вместе с любыми двумя точками соединяющий их отрезок.

28. Докажите, что пересечение двух выпуклых множеств u,V ⊂r2 является выпуклым множеством

Ответ: Пусть U,V – выпуклые на выпуклом множестве R² и точки A,B R²

Вычислим:

(U+V)(αA+(1-α)B)=U(αA+(1-α)B) + V(αA+(1-α)B)≤αU(A)+(1-α)U(B) + αV(A)+(1-α)U(B)=α(U(A)+V(A))+(1-α)(U(B)+V(B))=α(U+V)(A)+(1-α)(U+V)(B) для всех α [0;1]

29. Дайте определение выпуклой функции нескольких переменных. Докажите, что если функции f(x) и g(x), определенные на выпуклом множестве X Rⁿ, являются выпуклыми, то их сумма f(x)+g(x) – также выпуклая функция.

Ответ: Функция f(x), определенная на выпуклом множестве X из Rⁿ, называется выпуклой, если для любых векторов a,b из X и любого α [0;1] выполняется неравенство

F(αa + (1-α)b) ≤αf(a) + (1-α)f(b)

Пусть A – выпуклая область и функции f(x) и g(x) выпуклы в A. Тогда сумма этих функций h(x)=f(x)+g(x) также выпукла в A.

Док-во: Пусть x1 и x2 принадл. A и x3=s*x1+(1-s)*x2, где s [0;1]. Тогда h(x3)=f(x3)+g(x3)=f(s*x1+(1-s)*x2) + g(s*x+(1-s)*x2)=s(f(x1)+g(x1)) + (1-s)* *(f(x2)+g(x2))=s*h(x1) + (1-s)*h(x2), что и означает выпуклость функции h.

30. Сформулируйте теорему о сведении двойного интеграла к повторному. Докажите, что если функции f(x) и g(y) непрерывны на отрезках [a,b] и [c,d] соответственно, то = * , где G={(x,y)| a≤x≤b, c≤y≤d}

Ответ: Пусть область G – криволинейная трапеция, ограниченная линиями x=a, x=b (a≤b), y=g1(x), y=g2(x) (g1(x)≤g2(x) при x [a,b])

Если f(x,y) интегрируема на G и при любом фиксированном x [a,b] существует интеграл , то верна формула =

31. Сформулируйте теорему о замене переменных в двойном интеграле. Перейдите к полярным координатам в интеграле , где G={(x,y)|x²+y²≤9}

Ответ: Пусть непрерывно дифференцируемые функции х = х(u; v); у = у(u; v) осуществляют однозначное отображение ограниченной и замкнутой области Р в плоскости Оху на область Р' в окрестности Ouv. Если якобиан

= сохраняет постоянный знак в Р, то справедлива формула =

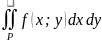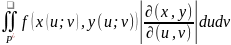
В случае перехода к полярным координатам r и γ: x=rcosγ; y=rsinγ, получаем

=

32. Дайте определение линейного дифференциального уравнения. Докажите, что если y₁(x) и y₂(x) – решения линейного неоднородного дифференциального уравнения, то их разность y₁(x)-y₂(x) является решением соответствующего однородного уравнения.

Ответ: Линейным дифференциальным уравнением называется уравнение вида y⁽ⁿ⁾+p₁(x)y^(n-1)+…+p_n(x)y=f(x), где y=y(x) – искомая функция, y⁽ⁿ⁾,y^(n-1),…,y’ – ее производные, а p₁(x), p₂(x), …, p_n(x) (коэффициенты) и f(x) (свободный член) – заданные функции.

Док-во:

33. Дайте определение линейно независимой системы функций. Докажите линейную независимость системы y=e^-x, y=e^x, y=e^2x на R.

Ответ:

34. Докажите линейную зависимость системы функций y=1, y=x-2, y=x+2 на R.

Ответ: