
- •1. Дайте определение расстояния ρ(a,b) между точками a,b∈r. Сформулируйте и докажите свойства функции ρ(a,b).
- •8. Как связаны производная по направлению и градиент дифференцируемой функции f(X,y)? Чему равна производная по направлению, перпендикулярному градиенту?
- •9. Дайте определение градиента функции f(X,y) в точке (x0,y0). Докажите, что в направлении градиента происходит наиболее быстрый рост функции. Чему равна скорость этого роста?
- •10. Дайте определение однородной функции степени α
- •11. Приведите пример однородной функции f(X,y) степени 3, не являющейся рациональной функцией.
- •15. Дайте определения числового ряда и его суммы. Найдите, исходя из определения, сумму ряда …
- •16. Сформулируйте и докажите необходимое условие сходимости числового ряда. Приведите пример расходящегося ряда, для которого это условие выполнено.
- •19. Сформулируйте и докажите признак Даламбера для числовых рядов с положительными членами
- •20. Сформулируйте признак Даламбера в предельной форме. Приведите пример сходящегося ряда с положительными членами, к которому этот признак неприменим.
- •21. Дайте определение гармонического ряда. Докажите, что гармонический ряд расходится.
- •22. Сформулируйте признак Лейбница для знакочередующихся числовых рядов. Приведите пример знакочередующегося ряда, сходящегося условно.
- •27. Дайте определение выпуклого множества в Rn. Приведите примеры выпуклых множеств в r2, объединение которых: а) является выпуклым множеством; б) не является выпуклым множеством.
- •28. Докажите, что пересечение двух выпуклых множеств u,V ⊂r2 является выпуклым множеством
19. Сформулируйте и докажите признак Даламбера для числовых рядов с положительными членами
Ответ:
Признак
Даламбера: Если для ряда a1+a2+…+an+…
с положительными членами существует
предел L=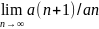 ,
то при 0<L<1 ряд сходится, а при L>1 –
расходится. Замечание: при L=1 признак
ответа не дает.
,
то при 0<L<1 ряд сходится, а при L>1 –
расходится. Замечание: при L=1 признак
ответа не дает.
Док-во:
Пусть L<1.
Тогда для ε=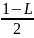 >0
существует n0,
такое что
>0
существует n0,
такое что
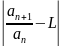 <
ε= =
<
ε= =
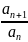 –L<
;
<
–L<
;
<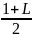 = q
= q
Тогда q<1, т.к. L<1
Имеем:
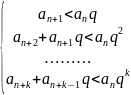
В силу первого признака сравнения рядов из сходимости ряда an+anq+…+anqk+… при 0<q<1 следует сходимость ряда an+an+1+…+an+k+…
Док-во закончено. Для случая L>1 док-во аналогично, но получается сравнением с суммой геом. прогрессии, где q>1
20. Сформулируйте признак Даламбера в предельной форме. Приведите пример сходящегося ряда с положительными членами, к которому этот признак неприменим.
Ответ:
Если существует
p= ,
то рассматриваемый ряд абсолютно
сходится если p<1, a
если p>1 – расходится.
,
то рассматриваемый ряд абсолютно
сходится если p<1, a
если p>1 – расходится.
Пример
ряда:
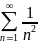
21. Дайте определение гармонического ряда. Докажите, что гармонический ряд расходится.
Ответ: Ряд 1+1/2+1/3+…+1/n+…
называется гармоническим. Для этого ряда не выполняется условие сходимости.
Т: Гармонический ряд расходится
Док-во: Допустим, что ряд сходится и его сумма равна S. Тогда,
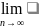 (S2n-Sn)=S-S=0
(S2n-Sn)=S-S=0
C другой стороны,
(S2n-Sn)=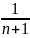 +
+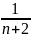 +…+
+…+ >
(при n>1)
>
+…+
(n
раз) = n*
=1/2
>
(при n>1)
>
+…+
(n
раз) = n*
=1/2
Предел в этом случае если и существует, то он ≥ ½. Имеет место противоречие => теорема доказана.
22. Сформулируйте признак Лейбница для знакочередующихся числовых рядов. Приведите пример знакочередующегося ряда, сходящегося условно.
Ответ: Если абсолютные величины an членов ряда
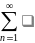 (-1)n-1an,an>0,
монотонно убывая, стремятся к нулю,
т.е. An+1<an
и lim
(n
(-1)n-1an,an>0,
монотонно убывая, стремятся к нулю,
т.е. An+1<an
и lim
(n )
an=0,
то исходный ряд сходится. При этом любой
остаток rk=
)
an=0,
то исходный ряд сходится. При этом любой
остаток rk=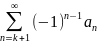 ряда не превосходит по модулю первого
из своих членов, т.е. |rk|≤ak+1
ряда не превосходит по модулю первого
из своих членов, т.е. |rk|≤ak+1
Пример:

23.
Сформулируйте теорему Абеля для
степенных рядов. Может ли ряд
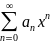 ,
расходящийся в точке x=
-2, сходиться
при x=3?
,
расходящийся в точке x=
-2, сходиться
при x=3?
Ответ: Если степенной ряд a0+a1*x+a2*x2+…+an*xn+… (1) сходится при некотором x=x0, не равном нулю, то он абсолютно сходится при всех x, удовлетворяющих условию |x|<|x0|. Если ряд расходится при некотором x=x1, то он расходится при всех x, удовлетворяющих условию |x|>|x1|
Нет,
такой ряд не может сходиться, т.к. если
при x=3 он сходится, то он должен сходиться
при всех х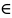 (-3;3)
(-3;3)
24.
Сформулируйте теорему о почленном
дифференцировании степенного ряда.
Используя эту теорему, найдите сумму
ряда
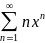 при |x|<1
при |x|<1
Ответ: Пусть функция f(x) на интервале (-R,R) разлагается в степенной ряд f(x)=a0+a1*x+a2*x2+…+anxn+… (1). Рассмотрим степенной ряд
a1+2a2*x+…+nan*xn-1 (1'), полученный почленным дифференцированием этого ряда. Тогда:
1) Ряд (1') имеет тот же радиус сходимости R, что и ряд (1)
2) на всем интервале (-R,R) функция f(x) имеет производную f'(x), которая разлагается в степенной ряд (1')
25. Сформулируйте достаточное условие разложимости функции в ряд Маклорена. Докажите, что функция f(x)=sinx разлагается в ряд Маклорена на любом интервале (-a,a).
Ответ: Пусть функция f(x) определена и бесконечно дифференцируема на интервале (-r,r). Если существует такая константа M, что во всех точках указанного интервала выполняются неравенства |f(n)(x)|<M (n=0,1,2,…), то в этом интервале ряд Маклорена сходится к функции f(x).
26. Докажите, что функция f(x)=ex разлагается в ряд Маклорена на всей числовой оси.
Ответ:
