9. Дайте определение градиента функции f(X,y) в точке (x0,y0). Докажите, что в направлении градиента происходит наиболее быстрый рост функции. Чему равна скорость этого роста?

Ответ: Под градиентом функции f(x,y) понимается вектор-функция, проекциями которой являются ее соответствующие частные производные, т.е.

f(M) = ( , ).

Теорема: Градиент указывает направление наискорейшего возрастания ф-ии, а максимальная скорость этого возрастания равна модулю градиента

Док-во: В силу равенства (M)=( f(M), ) имеем (M) =| f(M)|* |*cosγ (1), где γ – угол между вектором градиента и направлением .

C другой стороны, =1, а cos γ≤1. Следовательно, из (1) имеем

(M) ≤| f(M)|

В случае γ=0 из (1) получим, что производная по направлению в точке М совпадает с градиентом.

10. Дайте определение однородной функции степени α

Ответ: Функция f(x,y) называется однородной функцией степени α, если при всех t выполняется тождество f(tx,ty)=t^kf(x,y)

11. Приведите пример однородной функции f(X,y) степени 3, не являющейся рациональной функцией.

Ответ:

12. Дайте определение локального экстремума функции двух переменных. Является ли равенство нулю частных производных функции в некоторой точке достаточным условием ее локального экстремума в этой точке?

Ответ: Точка А=(a,b) ∈R² называется точкой локального минимума [максимума] ф-ии f(x,y), если существует ε-окрестность U_ε(a), в котором верно неравенство:

f(x,y)≤f(A) [f(x,y)≥f(A)]

Равенство нулю частных производных не есть достаточное условие локального экстремума, т.к. в этом случае ΔP=0, чему не соответствует ни случай локального максимума, ни случай локального минимума

13-14. Решение заданий

15. Дайте определения числового ряда и его суммы. Найдите, исходя из определения, сумму ряда …

Ответ: Пусть дана числовая последовательность {a_n}. Числовым рядом называется формальная бесконечная сумма, т.е

a₁+a₂+…+a_n+… =

Суммой ряда называется сумма всех его членов.

16. Сформулируйте и докажите необходимое условие сходимости числового ряда. Приведите пример расходящегося ряда, для которого это условие выполнено.

Ответ: Необходимый признак сходимости: Пусть числовой ряд a₁+a₂+…+a_n+… сходится, а S – его сумма. Тогда при неограниченном возрастании числа n членов ряда его общий член a_n стремится к нулю

Док-во: Так как S_n-S_n-1=a_n и a_n0, то =S и =S

Поэтому =

= - =S-S=0

Пример:

ln(1+ )+ln(1+ )+…+ln(1+ )+…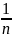

ряд расходится, хотя общий член стремится к нулю при n∞

17. Докажите, что если ряд , a­_n≥0, а ряд расходится, то ряд расходится

Ответ:

18. Докажите, что для сходимости ряда , a_n≥0 необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена

Ответ: Для того, чтобы ряд с неотрицательными членами сходился, необходимо и достаточно, чтобы последовательность частичных сумм этого ряда была ограничена.

Док-во: Необходимость: Пусть ряд сходится. Это значит, что последовательность его частичных сумм имеет предел. Всякая сходящаяся последовательность является ограниченной

Достаточность: Пусть последовательность частичных сумм ряда ограничена. Т.к. ряд с неотрицательными членами, то его частичные суммы образуют не убывающую последовательность: 0≤S₁≤S₂≤…≤S_n-1≤S_n≤…

Монотонная ограниченная последовательность сходится, т.е. сходится ряд