Задание №2. Статистический анализ данных.

Даны результаты эксперимента (файл DATA_1).

1. Найти среднее значение выборки, медиану, моду, стандартное отклонение, максимальное и минимальное значения.

2. Построить гистограмму распределения данных.

Произведем чтение из файла, транспонируем и отсортируем полученные данные.

Таким образом: x₀<x_1, x₁<x_2,...,x_i<x_i+1.

Функции в MathCad:

Среднее арифметическое – это отношение суммы всех данных к их количеству:

X_cp=∑Xi/N_A

В MathCad находится при помощи функции mean(А), где А-элементы массива.

Медиана – это значение, при котором площадь под графиком функции делится пополам:

Определяется функцией median(А), где А-массив.

Мода – наиболее встречающееся значение среди представленных данных. Определяется функцией mode(А), где А-массив.

где x_(M0)-нижняя граница модального интервала; h_(M0)-величина модального интервала; f_(M0)-1, f_(M0)+1-частоты соответственно в предыдущем и за следующим модальным интервалах.

Максимальное и минимальное значения найдем при помощи функций max и min.и

Стандартное отклонение показывает, насколько широко значения рассеяны от среднего значения. Находится при помощи функции stdev(А), где А-массив.

Гистограмма – инструмент, который позволяет наглядно изобразить и легко выявить структуру и характер изменения полученных данных (оценить распределение), которые трудно заметить при их табличном представлении. Hist(n,y)-функция построения гистограммы массива А.

Построим гистограмму распределения данных для 5 интервалов.

При нахождении моды выдается ошибка, поскольку все значения повторяются только один раз.

Построение гистограммы:

Задание№3.Решениедифференциальныхуравнений.

Тело в виде шара находится в воде и в начальный момент времени имеет скорость v(0)=10 м/с. Радиус шара R=0,02. Уравнение движения тела в жидкости имеет следующий вид:

где k – коэффициент сопротивления, для шара k=6πRŋ. Для воды ŋ=0,01. Масса шарика m=0,03 кг. Необходимо решить дифференциальное уравнение, построить график изменения скорости, определить время до полной остановки тела. Повторить решение для случая движения тела в воздухе, ŋ=1,88∙10^-4.

Определение решения дифференциального уравнения аналитически не всегда является возможным, в связи с тем были разработаны методы приближенного решения.

Нахождение приближенных решений возможно с помощью степенных рядов или с помощью численных методов.

Дифференциальное уравнение первого порядка, разрешенное относительно производной, имеет вид:

y´=f(x,y). (1)

Решением этого дифференциального уравнения является функция p(x), подстановка которой в уравнение обращает его в тождество: p´(x) = f(x,(p(x)). График решения y=p(x) называется интегральной кривой. Например, решением уравнения у' = у является функция p(x)=Ce^x при любом значении произвольной постоянной С.

Задача Коши для дифференциального уравнения состоит в том, чтобы найти решение этого уравнения, удовлетворяющее начальному условию

y_x=x0=y₀. (2)

Пару чисел (хо, уо) называют начальными данными. Решение задачи Коши называется частным решением уравнения (1) при условии (2). Например, частным решением задачи Коши y´=y, y_x=0=1 является функция p(х) = е^x .

Простейшим численным методом решения задачи Коши (1)-(2) является метод Эйлера, называемый иногда методом ломаных Эйлера. Пусть задано дифференциальное уравнение (1) с начальным условием y(x₀)=y₀ (задача Коши). Выбрав достаточно малый шаг h можно определить систему равноотстоящих точек: x_i=x₀+i*h (i=0, 1, 2, …)

Интегральная кривая y=y(x) являющаяся решением, фактически заменяется ломаной линией проходящей через точки M_i(x_i,y_i). Значения y_i могут быть определены по формулам: y_i+1=y_i+Δy_i, Δy_i=h*f(x_i,y_i) (i=0, 1, 2, …)

Метод Эйлера является простейшим численным методом интегрирования дифференциальных уравнений. Недостатки метода Эйлера:

1. Недостаточная точность;

2. Систематическое накопление ошибок.

Метод Рунге-Кута является более точным методом решения дифференциальных уравнений. Рассмотрим применение данного метода для решения задачи Коши (1). Пусть выбран шаг h, соответственно x_i=x₀+i*h; y_i=y(x_i) (i=0, 1, 2, …). Последовательные значения искомой функции определяется по формуле y_i+1=y_i+Δy_i,

где

В этом уравнении числа k₁, k_2, k₃, k₄ определяются следующим образом:

Погрешность метода Рунге-Кута на каждом шаге есть величина порядка h⁵, исходя из этого, данный метод называют методом Рунге-Кута пятого порядка.

Кроме приведенных методов существуют и другие методы: Адамса, Крылова, Милна, модификации метода Эйлера.

В MathCad для решения дифференциальных уравнений существуют специальные функции и вычислительный блок Given-Odesolve, с помощью которой может быть решена как задача Коши для обыкновенного дифференциального уравнения, так и граничная задача. В данном блоке реализован метод Рунге-Кута с постоянным шагом. Эта функция входит в состав блока решения и является его заключительным ключевым словом.

Odesolve(x,b,[step]) -Возвращает функцию, которая является решением дифференциального уравнения. Используется в блоке с оператором Given. x –переменная интегрирования, действительное число b –конечная точка отрезка интегрирования step -величина шага по переменной интегрирования (необязательный аргумент)

Замечания:

1. Уравнение должно быть линейным относительно старшей производной.

2. Число заданных начальных или граничных условий внутри блока должно быть равно порядку уравнения.

3. При записи уравнения для обозначения производных функции используйте специальные кнопки с панели Math или ' (штрих) - [Ctrl+F7], для знака равенства = [Ctrl+=] (в том числе и для дополнительных условий).

4. Конечная точка должна быть больше начальной.

5. Не допускаются начальные и граничные условия смешанного типа f '(a)+f(a)=5.

6. Искомая функция в блоке должна быть обязательно с аргументом (f(x))

Запишем все необходимые данные, рассчитаем k для воды, решим уравнение, и построим график функции v(t). Затем определим значение t с точностью до 0,001(для воды) и 0,01(для воздуха), при котором v(t)=0. Повторим расчеты для движения шарика в воздухе.

Для воды:

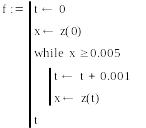
Шарик остановится в момент времени t=60,487 с.

Для воздуха:

Шарик остановится в момент времени t=2568 c.

Задание №4. Обработка данных.

Исходные экспериментальные данные для выполнения задания содержатся в файле data4_1.txt. В первой строке содержатся значения абсцисс точек, во второй содержатся их ординаты. Для заданных экспериментальных данных необходимо выполнить:

– линейную интерполяцию;

– кубическую интерполяцию;

– провести регрессивный анализ и определить порядок полинома, наилучшим способом описывающего экспериментальные данные;

– определить площадь под кривой в диапазоне от минимального до максимального значений абсцисс точек (для всех функций интерполяции);

– построить графики первой производной.

Рассмотрим некоторые методы численного анализа.

Интерполирование функций:

Пусть функция y=f(x) определена таблицей. Значения аргументов {x_i} (i=0, 1, …, n)

xi	x0	x1	…	xn
yi	y0	y1	…	yn

будем называть узлами интерполяции. Задачей интерполяции является построение многочлена P(x), значения которого в узлах интерполяции x_i равны соответствующим значениям заданной функции, т.е. P(x_i)=y_i (i=0, 1, …, n).

Линейная интерполяция:

Способ приближенного вычисления значения функций  f(x), основанный на замене функции f(х), линейной функцией:  L(x)=a(x-x₁)+b параметры а и b к-рой выбираются таким образом, чтобы значения L(х).совпадали со значениями f(x).в заданных точках х ₁ и х ₂:

L(x₁)=f(x₁), L(x₂)=f(x₂)

Этим условиям удовлетворяет единственная функция

,

приближающая заданную функцию f(х) на отрезке [x₁ , x₂]с погрешностью 

, wϵ(x₁,x₂).

Для построения линейной интерполяции достаточно на каждом из интервалов (x_i,x_i+1) вычислить уравнение прямой, проходящей через эти две точки.

Кубическая сплайн-интерполяция:

В большинстве практических приложений желательно соединить экспериментальные точки (x_i,y_i) не ломаной линией, а гладкой кривой. Лучше всего для этих целей подходит интерполяция у(x) квадратичными или кубическими сплайнами, т. е. отрезками квадратичных или кубических парабол.

Смысл сплайн-интерполяции заключается в том, что в каждом промежутке между узловыми точками осуществляется аппроксимация в виде зависимости A(t)=a*t³+b*t²+c*t+d. Коэффициенты a,b,c,d рассчитываются независимо для каждого промежутка, исходя из значений y_i в соседних точках. Участки парабол называются сплайнами. Сплайн-интерполяция обеспечивает равенство в узлах не только самих соседних параболических интерполирующих функций (сплайнов), но и их 1-х производных. Благодаря этому сплайн-интерполяция выглядит как очень гладкая функция.

Для построения кубической сплайн-интерполяции на i-м интервале, т.е. между узлами (t_i,t_i+1 ), используются формулы: 

где