
2) , То ряд сходится
Рассмотрим
 при n
при n

Следовательно,
 убывает.
убывает.

Значит ряд сходится по признаку Лейбница.
Ответ: сходится.
Задача 8.
Вычислить
сумму ряда с точностью



Обозначим
n-ный
член ряда, как


Чтобы
вычислить сумму ряда с заданной точностью,
следует принять во внимание то, что
члены ряда с ростом n
монотонно убывают. Тогда нам требуется
найти сумму ряда до N-го
члена таково, что для любых n выполняется неравенство
выполняется неравенство
 Найдем N:
Найдем N:






Найдем сумму ряда до 6-го члена:

Ответ:
Задача 9.
Найти область сходимость ряда:

Обозначим
 ,
а искомую область сходимости ряда –X
,
а искомую область сходимости ряда –X
Пусть
 тогда получим, что при n
тогда получим, что при n ,
следовательно, ряд расходится на данном
множестве
,
следовательно, ряд расходится на данном
множестве .
(Необходимым условием сходимости ряда
является стремление
.
(Необходимым условием сходимости ряда
является стремление
 к
нулю при стремлении n
к бесконечности.
к
нулю при стремлении n
к бесконечности.
При
 ,
тогда сделаем замену переменных:
,
тогда сделаем замену переменных:
x= , тогда
, тогда
 Подставим t
вместо x
в ряд:
Подставим t
вместо x
в ряд:

Получаем,
что для любого фиксированного x=
 и
поэтому ряд сходится.
и
поэтому ряд сходится.
Так
как мы провели все возможные x
на принадлежность области сходимости,
то, в итоге, X=
Ответ: область сходимости
Задача 10.
Найти область сходимости ряда:

Приведем этот ряд к степенному виду:
 ,
где
,
где
 не
зависит от x
и является постоянной величиной.
не
зависит от x
и является постоянной величиной.
Положим
 ,
,
 ,
тогда исходный ряд можно переписать в
виде:
,
тогда исходный ряд можно переписать в
виде:

Используем формулу для нахождения радиуса сходимости, основанную на применении признака Коши:
R=
Таким образом, интервал сходимости ряда будет выглядеть следующим образом:
-1 +3
+3
Ответ:
Область сходимости ряда X=
Задача 11.
Найти область сходимости ряда:

Найдем этот ряд к степенному, т.е. к виду: , где не зависит от x и является постоянной величиной.
Положим
 тогда исходный ряд можно переписать в
виде:
тогда исходный ряд можно переписать в
виде:

Теперь нам требуется найти:

Воспользуемся следующим равенством:
 где
a
и b
постоянные числа, a
где
a
и b
постоянные числа, a
Тогда.

Таким
образом, по теореме Коши-Адамара, область
сходимости X=
Решим неравенство, чтобы в явном виде записать область сходимости:

Решим
уравнение

D=36-13 =-16
=-16
Т.к. дискриминант меньше нуля, то:



Ответ:
область сходимости X=
Задача 12.
Найти область сходимости ряда:

Проведем тождественные преобразования ряда:

Теперь
преобразуем ряд
 в эквивалентный:
в эквивалентный:

Для ряда

Подставим преобразованные ряды в исходный ряд:

Обозначим
А(x)=
Рассмотрим
производную


(Сумма убывающей геометрической прогрессии.)
Ряд
будет сходиться при

А(x)=
Чтобы найти константу С, найдем значение ряда в некоторой фиксированной точке x, возьмем x=0, тогда А(x)=0=С,
Таким
образом, сумма ряда A(x)= есть –x-ln(1-x)
при
есть –x-ln(1-x)
при
 ,
и не существует при всех остальных x.
,
и не существует при всех остальных x.
Получаем:

Ответ:
Задача 13.
Найдите сумму ряда:
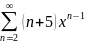
Разложим этот ряд на сумму двух более простых рядов:

Найдем
А(x)= Заметим, что А(x)
есть производная от функции B(x)=
Заметим, что А(x)
есть производная от функции B(x)=
 ,
умноженная на x:
,
умноженная на x:
 (x)=
(x)=
A(x)=x
Сумма
ряда B(x)
есть сумма убывающей геометрической
прогрессии и поэтому равна B(x)= ,
при условии, что
Тогда производная от B(x)
такова:
,
при условии, что
Тогда производная от B(x)
такова:
(x)=
Тогда
A(x)=x
=x при
и не существует при
при
и не существует при


Ответ:

Задача 14.
Разложить функцию в ряд Тейлора по степеням X:

Чтобы решить эту задачу, следует воспользоваться табличными разложениями и степенные ряды. Приведем функцию к виду, удобному для разложения:

Воспользуемся
табличным разложение для


Ряд полученный нами, еще не является рядом Тейлора по степеням x. Следует воспользоваться табличными разложениями еще раз, Для это преобразуем функцию следующим образом:

Воспользуемся
табличным разложением для


Положим
m=k+n.
Т.к. k,
n
 то
0
то
0 0
0 Из определения k
следует, что
Из определения k
следует, что
 Теперь
найдем все возможные комбинации k
и
Теперь
найдем все возможные комбинации k
и
 чтобы m=k+n,
где m-
произвольное фиксированное число, m
чтобы m=k+n,
где m-
произвольное фиксированное число, m Т.к.
Т.к.
 ,
то
,
то
 т.е.
т.е.

Найдем
коэффициент перед
 n
раскладывается на сумму n
и k
несколькими способами, то
n
раскладывается на сумму n
и k
несколькими способами, то
 где суммирование ведется по всем
допустимым парам(n,k).
Выразим индексы n
и k
через m:
n=m-k
где суммирование ведется по всем
допустимым парам(n,k).
Выразим индексы n
и k
через m:
n=m-k
Итого:

Тогда:
f(x)=
Ответ:

