1. Предмет динамики. Основные законы механики. Динамика – раздел механики, в котором изучаются законы движения материальных тел под действием сил. Предметом динамики является изучение движения материальных точек, тел и их систем с учетом действующих сил. Силы в динамике переменные и могут зависеть от времени, положения тела и от его скорости.

К понятию инертности можно придти, если сравнить результаты действия одной силы на разные тела. Свойство тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил называется инертностью.

Количественной мерой инертности является масса тела. Массу данного тела будем считать постоянной (за исключением особо обговариваемых случаев). Чтобы отвлечься от формы тела вводится понятие материальной точки.

Материальной точкой называется материальное тело, имеющее массу, размерами которого при изучении движения можно пренебречь. В динамике тело, движущееся поступательно можно считать материальной точкой.

В основе динамики лежат законы, которые изложил Ньютон в 1687 году. Эти три закона называют еще аксиомами Галилея-Ньютона, так как первый закон был открыт Галилеем еще в 1638 году.

Законы механики: 1. Закон инерции: изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные силы не заставят ее изменить свое состояние. Движение, совершаемое точкой при отсутствии сил, называется движением по инерции.

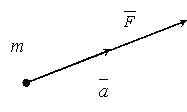
2. Основной закон динамики. Он устанавливает, как изменяется скорость точки при действии на нее какой-нибудь силы. Он гласит: произведение массы точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы. am=F, a – ускорение, m – масса, F – сила. Если на точку действует одновременно несколько сил, то они будут эквивалентны однной силе, т.е. равнодействующей R, равной геометрической сумме этих сил. Уравнение, выражающее основной закон динамики, примет в этом случае вид:

am=R или am=∑F_k

На все тела, находящиеся вблизи земной поверхности, действует сила тяжести P, численно равная весу тела. P=mg, g – ускорение свободного падения.

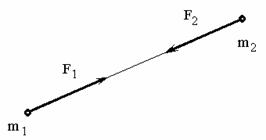
3. Закон равенства действия и противодействия. Он устанавливает характер механического взаимодействия между материальными телами. Для двух материальных точек он гласит: две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль одной прямой, соединяющей эти точки, в противоположные стороны.

2. Теорема об изменении количества движения механической системы. Понятия импульса силы, количество движения механической системы. Основными динамическими характеристиками движения точки являются количество движения и кинетическая энергия.

Количесво движения системы – векторная величина Q, равная геометрической сумме (главному вектору) количеств движения всех точек системы. Направлен вектор Q так же, как и скорость точки, т.е. по касательной к ее траектории. Q= .

Для характеристики действия, оказываемого на тело силой за некоторый промежуток времени, вводится понятие об импульсе силы. Введем сначала понятие об элементарном импульсе, т.е. об импульсе за бесконечно малый промежуток времени dt. Элементарный импульс силы – это векторная величина dS, равная произведению вектора силы F на элементарный промежуток времени dt: dS=Fdt.

Направлен элементарный импульс по линии действия силы.

Импульс S любой силы F за конечный промежуток времени t₁ вычисляется как интегральная сумма соответствующих элементарных импульсов: S=

Следовательно, импульс силы за любой промежуток времени t₁ равен определенному интегралу от элементарного импульса, взятому в пределах от нуля до t₁.

Теорема об изменении количества движения механической системы:

Изменение количества движения системы за некоторый промежуток времени равняется геометрической сумме импульсов, действующих на систему внешних сил, за тот же промежуток времени. Q₁ - Q₀= или Q₁ - Q₀₌ , где F^e – внеш. сила

Теорема позволяет исключить из рассмотрения заведомо неизвестные внутренние силы.

3. Дифференциальные уравнения движения свободной материальной точки в декартовой и естественной системах координат.

Свободной называют точку, на которую не наложены связи. В противном случае точка является несвободной и тогда, согласно принципу освобождаемости от связей к точке прикладывают реакции отброшенных связей, кроме активных сил.

Декартовой обычно называют прямоугольную систему координат с одинаковыми масштабами по осям (оси x и y).

Естественная система координат: с осями x, y, z.

Из кинематики известно, что движение точки в прямоугольных декартовых

координатах задается уравнениями: , ,

Зная, что a_x= a_y= , a_z=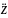 получим диффер-е ур-я в дек-ой системе координат: , ,

Диф-е ур-я в ест-й системе координат: , ,

(Где - тангенсальное ускорение, - нормальное ускорение, - бинормальное ускорение)

4. Закон сохранения количества движения механической системы.

1. Если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянен по модулю и направлению. Т.е. если =0, то Q=const

2. Если сумма проекций всех действующих внешних сил на какую-нибудь ось (например О_x) равна нулю, то проекция количества движения системы на эту ось есть величина постоянная. Т.е. если , то Q_x=const

Из этого следует, что внутренние силы не могут изменить суммарное количество движения системы.

5. Две основные задачи динамики точки. Формулировка и примеры

Первая задача динамики состоит в том, чтобы при известных массы точки и законе ее движения найти величину и направление силы, действующие на точку (задача дифференцирования).

Можно предложить такую последовательность решения задачи:

1) выбрать систему координат, в которой удобно решать данную задачу (декартовую или естественную);

2) изобразить в выбранной системе координат материальную точку в текущем положении;

3) приложить к точке активные силы и реакции связей;

4) записать основное уравнение динамики в проекциях на оси выбранной системы координат;

5) найти проекции ускорения точки на оси выбранной системы координат путем дифференцирования уравнений ее движения;

6) определить искомые параметры с помощью системы составленных уравнений.

Вторая задача динамики заключается в том, чтобы по известной массе точки и силе действующей на нее, установить закон движения точки. Решение задачи сводится к интегрированию дифференциальных уравнений движения и определению постоянных интегрирования по начальным условия.

Методика решения второй задачи на примере декартовой системы координат состоит в следующем. Чтобы определить уравнения движения точки необходимо дважды проинтегрировать систему трех дифференциальных уравнений 2-го порядка. В результате получим уравнения движения точки, содержащие, кроме времени, шесть произвольных постоянных. Уравнения движения точки и проекции ее скорости на оси координат имеют вид:

где – это так называемые постоянные интегрирования, которые находят из начальных условий. Начальные условия – значение скорости (проекций скорости) и положения (координат) точки в момент времени, обычно принимаемый равным нулю, которые должны быть предварительно заданы:

После определения постоянных интегрирования уравнения действительного движения точки окончательно получим в виде:

Решение второй задачи динамики можно выполнить в такой последовательности:

1) выбрать систему координат (декартовую или естественную), в которой удобно решать данную задачу;

2) изобразить в выбранной системе координат материальную точку в текущем положении;

3) приложить к точке активные силы и реакции отброшенных связей (если точка несвободна);

4) записать основное уравнение динамики в проекциях на оси выбранной системы координат;

5) проинтегрировать полученную систему дифференциальных уравнений и найти их общие решения;

6) определить, использую заданные начальные условия, постоянные интегрирования;

7) подставить постоянные интегрирования в общие решения и получить действительные уравнения движения точки.