
- •11.2. Свойства определённого интеграла.
- •11.3. Вычисление определённого интеграла.
- •§43. Функции двух переменных
- •1.2.1. Понятие обыкновенного дифференциального уравнения.
- •1.2.2. Дифференциальное уравнение первого порядка.
- •1.2.3. Задача Коши.
- •1.2.4. Примеры дифференциальных уравнений первого порядка.
- •1.2.5. Общий интеграл дифференциального уравнения первого порядка.
- •1.2.6. Поле направлений.
- •§ 1.3. Простейшие дифференциальные уравнения первого порядка
- •1.3.1. Уравнение, записанное через дифференциалы.
- •1.3.2. Уравнения с разделенными переменными.
- •1.3.3. Уравнения с разделяющимися переменными.
- •1.3.4. Однородные уравнения.
- •1.3.5. Линейное уравнение.
- •27.1. Основные понятия
- •27.2. Геометрическое изображение комплексных чисел
- •27.3. Формы записи комплексных чисел
- •28.1. Сложение комплексных чисел
- •28.2 Вычитание комплексных чисел
- •28.3 Умножение комплексных чисел
- •28.4. Деление комплексных чисел
- •28.5. Извлечение корней из комплексных чисел
- •3.1.3. Полярная система координат.
1.3.2. Уравнения с разделенными переменными.
Уравнение (1) называется дифференциальным уравнением первого порядка с разделенными переменными, если

Оно имеет вид
![]() .
(4)
.
(4)
Далее
будем считать, что ![]() и
и ![]() -
непрерывные функции. Пусть
есть
решение дифференциального уравнения
(4) в прямоугольнике
-
непрерывные функции. Пусть
есть
решение дифференциального уравнения
(4) в прямоугольнике
![]() ,
,
определенное
на некотором интервале ![]() .
.
Тогда имеет место тождество
![]() ,
,
откуда, интегрируя, получим
![]() .
.
Здесь
интегралы ![]() и
и ![]() суть
некоторые выбранные нами первообразные
от
и
:
суть
некоторые выбранные нами первообразные
от
и
:

во
втором равенстве произведена замена
переменной ![]() в
неопределенном интеграле (см. вашу
книгу «Высшая математика. Дифференциальное
и интегральное исчисление», § 5.2);
константа
зависит
от решения
.
в
неопределенном интеграле (см. вашу
книгу «Высшая математика. Дифференциальное
и интегральное исчисление», § 5.2);
константа
зависит
от решения
.
Итак, любое решение нашего дифференциального уравнения в указанном прямоугольнике удовлетворяет уравнению
![]()
при некоторой постоянной или уравнению
![]() .
(5)
.
(5)
Левая
часть равенства (5) есть функция ![]() ,
непрерывно дифференцируемая на
прямоугольнике
,
непрерывно дифференцируемая на
прямоугольнике
![]() ,
,
со свойствами
![]() .
.
Если продифференцировать формально (5) по , считая, что , то получим
![]() ,
,
т. е. исходное дифференциальное уравнение (4).
Таким образом, равенство (5) есть общий интеграл дифференциального уравнения (4) для его решений вид . Согласно теореме 1 §1.2 все непрерывно дифференцируемые на решения уравнения (5) при любых постоянных являются решениями дифференциального уравнения (4) вида и обратно. Впрочем, обратное утверждение мы доказали непосредственно.
Рассуждая
аналогично, меняя местами роль
и
,
мы снова получим равенство (5), но только
теперь это будет общий интеграл,
содержащий всевозможные решения вида ![]() ,
нашего дифференциального уравнения
(4).
,
нашего дифференциального уравнения
(4).
Таким образом, равенство (5) будет общим интегралом дифференциального уравнения (4) как для решений вида , так и для решений вида .
Пример
1. ![]() .
.
![]() -
общий интеграл.
-
общий интеграл.
Пример
2.![]() .
.
Эти интегралы нельзя выразить в элементарных функциях. Все же мы считаем задачу, с точки зрения теории дифференциальных уравнений, решенной.
1.3.3. Уравнения с разделяющимися переменными.
Если ![]() ,
то уравнение (1) называется уравнением
с разделяющимися переменными:
,
то уравнение (1) называется уравнением
с разделяющимися переменными:
![]() (6)
(6)
Для
тех
для
которых ![]() ,
разделим на это произведение левую и
правую части (6). Тогда получим уравнение
с разделенными переменными
,
разделим на это произведение левую и
правую части (6). Тогда получим уравнение
с разделенными переменными
![]() .
.
Общий
интеграл этого уравнения находится,
как в 1.3.2. Но могут быть еще решения,
проходящие через точки
удовлетворяющие
уравнению ![]() .
.
1.3.4. Однородные уравнения.
Функция
называется
однородной степени ![]() ,
если для любых
,
если для любых ![]() и
и ![]() полняется
равенство
полняется
равенство
![]() .
.
Если функции и однородные одной и той же степени , то дифференциальное уравнение
![]() (7)
(7)
называется однородным.
Его можно преобразовать следующим образом
 ,
,
т.е.
![]() ,
(8)
,
(8)
где ![]() -
некоторая функция от одного переменного.
-
некоторая функция от одного переменного.
Введем
вместо
новую
функцию ![]() (от
)
при помощи подстановки
(от
)
при помощи подстановки
![]() .
.
Тогда
![]()
или
![]()
Следовательно,
![]()
или

где ![]() -
произвольная постоянная.
-
произвольная постоянная.
Отметим более общее уравнение, чем (8):
![]() .
(9)
.
(9)
Его можно решить подстановкой
![]() ;
;
тогда

![]() (10)
(10)
где - произвольная постоянная.
Пример
3. ![]() .
.
Данное уравнение является однородным, так как функции
![]()
однородные
степени ![]() .
Сделаем замену
.
Сделаем замену ![]() .
Тогда уравнение перепишется так:
.
Тогда уравнение перепишется так:
![]()
или
![]() .
.
Разделяя переменные, полдучаем
![]() .
.
Так
как у нас ![]() ,
то
,
то
 .
.
Пример 4.
![]() ,
(11)
,
(11)
 .
.
Это уравнение есть частный случай (9), если
![]() .
(12)
.
(12)
Уравнение
(11) при ![]() и
и ![]() (условие
(12) выполнено) имеет вид
(условие
(12) выполнено) имеет вид
![]() ,
,
и его решение записывается по формуле (10), где
![]() .
.
Полученное уравнение есть частный случай уравнения Риккати
,
которое
интегрируется в квадратурах только в
исключительных случаях. Мы доказали,
что при ![]() уравнение
Риккати решается в квадратурах. Отметим,
что при
уравнение
Риккати решается в квадратурах. Отметим,
что при ![]() уравнение
Риккати является уравнением с
разделяющимися переменными.
уравнение
Риккати является уравнением с
разделяющимися переменными.
Если
![]() и
и ![]() (
-
целое), то подстановка
(
-
целое), то подстановка
![]()
приводит уравнение Риккати к виду
![]()
Последовательно
применяя эту подстановку, можно исходное
уравнение свести к случаю ![]() .
.
Если
же ![]() ,
то подстановка
,
то подстановка
![]()
приводит уравнение к виду
![]()
Применяя
эту подстановку необходимое число раз,
мы сведем уравнение Риккати к случаю ![]() .
.
Во всех других случаях уравнение Риккати не решается в квадратурах.
Пример
5. ![]() .
.
Имеем
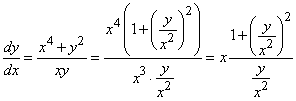 .
.
Это
уравнение есть частный случай уравнения
(9) при ![]() .
.
