
- •11.2. Свойства определённого интеграла.
- •11.3. Вычисление определённого интеграла.
- •§43. Функции двух переменных
- •1.2.1. Понятие обыкновенного дифференциального уравнения.
- •1.2.2. Дифференциальное уравнение первого порядка.
- •1.2.3. Задача Коши.
- •1.2.4. Примеры дифференциальных уравнений первого порядка.
- •1.2.5. Общий интеграл дифференциального уравнения первого порядка.
- •1.2.6. Поле направлений.
- •§ 1.3. Простейшие дифференциальные уравнения первого порядка
- •1.3.1. Уравнение, записанное через дифференциалы.
- •1.3.2. Уравнения с разделенными переменными.
- •1.3.3. Уравнения с разделяющимися переменными.
- •1.3.4. Однородные уравнения.
- •1.3.5. Линейное уравнение.
- •27.1. Основные понятия
- •27.2. Геометрическое изображение комплексных чисел
- •27.3. Формы записи комплексных чисел
- •28.1. Сложение комплексных чисел
- •28.2 Вычитание комплексных чисел
- •28.3 Умножение комплексных чисел
- •28.4. Деление комплексных чисел
- •28.5. Извлечение корней из комплексных чисел
- •3.1.3. Полярная система координат.
§43. Функции двух переменных
43.1. Основные понятия
Пусть задано множество D упорядоченных пар чисел (х;у). Соответствие ƒ, которое каждой паре чисел (х; у) є D сопоставляет одно и только одно число z є R, называется функцией двух переменных, определенной на множестве D со значениями в Е, и записывается в виде z = ƒ(х;у) или ƒ : D → R При этом х и у называются независимыми переменными (аргументами), а z — зависимой переменной (функцией).
Множество D = D(f) называется областью определения функции. Множество значений, принимаемых z в области определения, называется областью изменения этой функции, обозначается E(f) или Е.
Примером функции двух переменных может служить площадь S прямоугольника со сторонами, длины которых равны х и у: S = ху. Областью определения этой функции является множество {(х;у) | х > 0, у > 0}.
Функцию z = ƒ(х;у), где (х;у) є D можно понимать (рассматривать) как функцию точки М(х;у) координатной плоскости Оху. В частности, областью определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями. Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой, обозначается D. Примером замкнутой области является круг с окружностью.
Значение функции z = ƒ(х;у) в точке М0(х0;у0) обозначают z0=ƒ(хо;уо) или z0=ƒ(М0) и называют частным значением функции.
Ф ункция
двух независимых переменных допускает
геометрическое истолкование. Каждой
точке М0(х0;
у0)
области D в системе координат Oxyz
соответствует точка M(x0;y0;z0),
где z0 =
ƒ(хо;уо)
— аппликата точки М. Совокупность всех
таких точек представляет собой некоторую
поверхность, которая и будет геометрически
изображать данную функцию z=ƒ(x;у).
ункция
двух независимых переменных допускает
геометрическое истолкование. Каждой
точке М0(х0;
у0)
области D в системе координат Oxyz
соответствует точка M(x0;y0;z0),
где z0 =
ƒ(хо;уо)
— аппликата точки М. Совокупность всех
таких точек представляет собой некоторую
поверхность, которая и будет геометрически
изображать данную функцию z=ƒ(x;у).
Например,
функция![]() имеет
областью определения круг х2 +
у2 ≤
1 и изображается верхней полусферой с
центром в точке O(0;0;0) и радиусом R = 1 (см.
рис. 205).
имеет
областью определения круг х2 +
у2 ≤
1 и изображается верхней полусферой с
центром в точке O(0;0;0) и радиусом R = 1 (см.
рис. 205).
Функция двух переменных, как и функция одной переменной, может быть задана разными способами: таблицей, аналитически, графиком. Будем пользоваться, как правило, аналитическим способом: когда функция задается с помощью формулы.
43.2.
Предел функции
Для
функции двух (и большего числа) переменных
вводится понятие предела функции и
непрерывности, аналогично случаю функции
одной переменной. Введем понятие
окрестности точки. Множество всех точек
М(х;у) плоскости, координаты которых
удовлетворяют неравенству![]() называется -окрестностью
точки М0(х0;у0).
Другими словами, -окрестность точки
Мо —
это все внутренние точки круга с центром
Мо и
радиусом 8 (см. рис. 206).
называется -окрестностью
точки М0(х0;у0).
Другими словами, -окрестность точки
Мо —
это все внутренние точки круга с центром
Мо и
радиусом 8 (см. рис. 206).
Пусть функция z = ƒ(х; у) определена в некоторой окрестности точки М0(х0;у0), кроме, быть может, самой этой точки. Число А называется пределом функции z = ƒ (х; у) при х → х0 и у →у0 (или, что то же самое, при М(х; у) → М0(х0; у0)), если для любого є > 0 существует > 0 такое, что для всех х ≠ х0 и у ≠ у0 и удовлетворяющих неравенству
![]() выполняется
неравенство | ƒ (х; у) — А| < є. Записывают:
выполняется
неравенство | ƒ (х; у) — А| < є. Записывают:

Из определения следует, что если предел существует, то он не зависит от пути, по которому М стремится к Мо (число таких направлений бесконечно; для функции одной переменной х →х0 по двум направлениям: справа и слева!)
Геометрический смысл предела функции двух переменных состоит в следующем. Каково бы ни было число є>0, найдется -окрестность точки Mо(хо;уо), что во всех ее точках М(х;у), отличных от Мо, аппликаты соответствующих точек поверхности z=ƒ(х;у) отличаются от числа А по модулю меньше, чем на є.
Пример
43.1. Найти предел
Решение: Будем приближаться к О(0;0) по прямой у=Кх, где К — некоторое число. Тогда

Функция ![]() в
точке О(0; 0) предела не имеет, т. к. при
разных значенияхК предел функции не
одинаков (функция имеет различные
предельные значения).
в
точке О(0; 0) предела не имеет, т. к. при
разных значенияхК предел функции не
одинаков (функция имеет различные
предельные значения).
Предел
функции двух переменных обладает
свойствами, аналогичными свойствам
предела функции одной переменной (см.
п. 17.3). Это означает, что справедливы
утверждения: если функции ƒ (М) и g(М)
определены на множестве D и имеют в точке
Мо этого
множества пределы А и В соответственно,
то и функции ƒ(М) ± g(M), ƒ(М) • g(М), имеют в
точке Мо пределы, которые соответственно
равны![]() А
± В, А • В, A/B(В≠0).
А
± В, А • В, A/B(В≠0).
43.3. Непрерывность функции двух переменных
Функция z = ƒ(х;у) (или ƒ(М)) называется непрерывной в точке М0(х0;у0), если она:
а) определена в этой точке и некоторой ее окрестности,
б) имеет предел
в)
этот предел равен![]() значению
функции z в точке Мо, т.
е.
значению
функции z в точке Мо, т.
е.
![]()
Функция,
непрерывная в каждой точке некоторой
области, называется непрерывной в этой
области. Точки, в которых непрерывность
нарушается (не выполняется хотя бы одно
из условий непрерывности функции в
точке), называются точками разрыва этой
функции. Точки разрыва z=ƒ(х;у) могут
образовывать целые линии разрыва. Так,
функция ![]() имеет
линию разрыва у=х.
имеет
линию разрыва у=х.
Можно дать другое, равносильное приведенному выше, определение непрерывности функции z=ƒ(х;у) в точке. Обозначим Δх=х—х0, Δу=у—у0, Δz=ƒ(х;у)—ƒ(х0;у0). Величины Δх и Δу называются приращениями аргументов х и у, а Δz — полным приращением функции ƒ(х;у) в точке М0(х0;у0).
Функция
z = ƒ(х;у) называется непрерывной в точке
М0(х0;у0)
є D, если выполняется равенство![]() т.
е. полное приращение функции в этой
точке стремится к нулю, когда приращения
ее аргументов х и у стремятся к нулю.
т.
е. полное приращение функции в этой
точке стремится к нулю, когда приращения
ее аргументов х и у стремятся к нулю.
Пользуясь определением непрерывности и теоремами о пределах, можно доказать, что арифметические операции над непрерывными функциями и построение сложной функции из непрерывных функций приводит к непрерывным функциям — подобные теоремы имели место для функций одной переменной (см. п. 19.4).
43.4. Свойства функций, непрерывных в ограниченной замкнутой области
Приведем свойства функций, непрерывных в ограниченной замкнутой области (они аналогичны свойствам непрерывных на отрезке функций одной переменной — см. п. 19.5). Предварительно уточним понятие области.
Областью называется множество точек плоскости, обладающих свойствами открытости и связности.
Свойство открытости: каждая точка принадлежит ей вместе с некоторой окрестностью этой точки.
Свойство связности: любые две точки области можно соединить непрерывной линией, целиком лежащей в этой области.
Т очка
No называется
граничной точкой области D, если она не
принадлежит D, но в любой окрестности
ее лежат точки этой области. Совокупность
граничных точек области D называется
границей D. Область D с присоединенной
к ней границей называется замкнутой
областью, обозначается D. Область
называется ограниченной, если все ее
точки принадлежат неко торому кругу
радиуса R. В противном случае область
называется неограниченной. Примером
неограниченной области может служить
множество точек первого координатного
угла, а примером ограниченной —
(-окрестность точки М0(х0;у0).
очка
No называется
граничной точкой области D, если она не
принадлежит D, но в любой окрестности
ее лежат точки этой области. Совокупность
граничных точек области D называется
границей D. Область D с присоединенной
к ней границей называется замкнутой
областью, обозначается D. Область
называется ограниченной, если все ее
точки принадлежат неко торому кругу
радиуса R. В противном случае область
называется неограниченной. Примером
неограниченной области может служить
множество точек первого координатного
угла, а примером ограниченной —
(-окрестность точки М0(х0;у0).
Теорема 43.1. Если функция z = f(N) непрерывна в ограниченной замкнутой области, то она в этой области: а) ограничена, т. е. существует такое число R > О, что для всех точек N в этой области выполняется неравенство |f(N)| < R; б) имеет точки, в которых принимает наименьшее т и наибольшее М значения; в) принимает хотя бы в одной точке области любое численное значение, заключенное между m и М.
Теорема дается без доказательства.
44.1. Частные производные первого порядка и их геометрическое истолкование
Пусть задана функция z = ƒ (х; у). Так как х и у — независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной х приращение Δх, сохраняя значение у неизменным. Тогда z получит приращение, которое называется частным приращением z по х и обозначается ∆хz. Итак,
Δхz=ƒ(х+Δх;у)-ƒ(х;у).
Аналогично получаем частное приращение z по у:
Δуz=ƒ(x;у+Δу)-ƒ(х;у).
Полное приращение Δz функции z определяется равенством
Δz = ƒ(х + Δх;у + Δу)- ƒ(х; у).
Если существует предел

то он называется частной производной функции z = ƒ (х; у) в точке М(х;у) по переменной х и обозначается одним из символов:

Частные
производные по х в точке М0(х0;у0)
обычно обозначают символами![]()
Аналогичноопределяется и обозначается частная производная от z=ƒ(х;у) по переменной у:

Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции ƒ(х;у) находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х или у считается постоянной величиной).
Пример 44.1. Найти частные производные функции z = 2у + ех2-у +1. Решение:

Г еометрический
смысл частных производных функции двух
переменных
еометрический
смысл частных производных функции двух
переменных
Графиком функции z= ƒ (х; у) является некоторая поверхность (см. п. 12.1). График функции z = ƒ (х; у0) есть линия пересечения этой поверхности с плоскостью у = уо. Исходя из геометрического смысла производной для функции одной переменной (см. п. 20.2), заключаем, что ƒ'x(хо;уо) = tg а, где а — угол между осью Ох и касательной, проведенной к кривой z = ƒ (х; у0) в точке Мо(хо;уо; ƒ(хо;уо)) (см. рис. 208).
Аналогично, f'y (х0;у0)=tgβ.
44.2. Частные производные высших порядков
Частные
производные![]() называют
частными производными первого порядка. Их
можно рассматривать как функции от
(х;у) є D. Эти функции могут иметь частные
производные, которые называются частными
производными второго порядка. Они
определяются и обозначаются следующим
образом:
называют
частными производными первого порядка. Их
можно рассматривать как функции от
(х;у) є D. Эти функции могут иметь частные
производные, которые называются частными
производными второго порядка. Они
определяются и обозначаются следующим
образом:

Аналогично определяются частные производные 3-го, 4-го и т. д. порядков.
Так,![]() и
т.д.
и
т.д.
Частная
производная второго или более высокого
порядка, взятая по различным переменным,
называется смешанной
частной производной. Таковыми
являются, например,![]()
Пример 44.2. Найти частные производные второго порядка функции z = x4-2x2y3+y5+1.
Решение:
Так как![]() то
то

Оказалось,
что![]()
Этот результат не случаен. Имеет место теорема, которую приведем без доказательства.
Теорема 44.1 (Шварц). Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой.
В
настности, для z=ƒ(х; у) имеем:![]()
44.3. Дифференцируемость и полный дифференциал функции
Пусть функция z =ƒ (х; у) определена в некоторой окрестности точки М(х;у). Составим полное приращение функции в точке М:
![]()
Функция z = ƒ (х; у) называется дифференцируемой в точке М(х; у), если ее полное приращение в этой точке можно представить в виде
![]()
где а = а(Δх, Δу)→0 и β=β(Δх,Δу)→0 при Δх→0, Δу→0. Сумма первых двух слагаемых в равенстве (44.1) представляет собой главную часть приращения функции.
Главная часть приращение функции z=ƒ(х;у), линейная относительно Δх и Δу, называется полным дифференциалом этой функции и обозначается символом dz:
dz=A*Δx+B*Δy. (44.2)
Выражения А•Δх и В•Δу называют частными дифференциалами. Для независимых переменных х и у полагают Δх=dx и Δу=dy. Поэтому равенство (44.2) можно переписать в виде
dz=Adx+Bdy. (44.3)
Теорема 44.2 (необходимое условие дифференцируемости функции). Если функция z = ƒ(х;у) дифференцируема в точке М(х;у), то она непрерывна в этой точке, имеет в ней частные производные dz/dx и dz/dy, причем dz/dx = А, dz/dy = В.
Так
как функция дифференцируема в точке М,
то имеет место равенство (44.1). Отсюда
вытекает, что![]() Это
означает, что функция непрерывна в точке
М. Положив Δу = 0, Δх ≠ 0 в равенстве (44.1),
получим: Δz = А • Δх + а • Δх. Отсюда
находим
Это
означает, что функция непрерывна в точке
М. Положив Δу = 0, Δх ≠ 0 в равенстве (44.1),
получим: Δz = А • Δх + а • Δх. Отсюда
находим![]() Переходя
Переходя
к
пределу при Δх → 0, получим ![]()
Таким образом, в точке М существует частная производная ƒ'x(х;у) = А. Аналогично доказывается, что в точке М существует частная производная
![]()
Равенство (44.1) можно записать в виде
![]()
где =аΔх+βΔу→0 при Δх → 0, Δу → 0.
Отметим,
что обратное утверждение не верно, т.
е. из непрерывности функции или
существования частных производных не
следует дифференцируемость функции.
Так, непрерывная функция![]() не
дифференцируема в точке (0;0).
не
дифференцируема в точке (0;0).
Как следствие теоремы получаем формулу для вычисления полного дифференциала. Формула (44.3) принимает вид:

или
![]()
где![]() —
частные дифференциалы функции z=ƒ(х;у).
—
частные дифференциалы функции z=ƒ(х;у).
Теорема 44.3 (достаточное условие дифференцируемости функции). Если функция z = ƒ(х;у) имеет непрерывные частные производные z'x и z'y в точке М(х;у), то она дифференцируема в этой точке и ее полный дифференциал выражается формулой (44.5).
Примем теорему без доказательства.
Отметим, что для функции у=ƒ(х) одной переменной существование производной ƒ'(х) в точке является необходимым и достаточным условием ее дифференцируемости в этой точке.
Чтобы функция z=ƒ(х;у) была дифференцируема в точке, необходимо, чтобы она имела в ней частные производные, и достаточно, чтобы она имела в точке непрерывные частные производные.
Арифметические свойства и правила исчисления дифференциалов функции одной переменной сохраняются и для дифференциалов функции двух (и большего числа) переменных.
44.4. Применение полного дифференциала к приближенным вычислениям
Из определения дифференциала функции z=ƒ (х; у) следует, что при достаточно малых |Δх| и |Δу| имеет место приближенное равенство
![]()
Так как полное приращение Δz=ƒ(х+Δх;у+Δу)-ƒ(х;у), равенство (44.6) можно переписать в следующем виде:
![]()
Формулой (44.7) пользуются в приближенных расчетах.
Пример 44.3. Вычислить приближенно 1,023,01.
Решение:
Рассмотрим функцию z = ху. Тогда
1,023,01 =
(х + Δх)у+∆у, где х = 1, Δх = 0,02, у = 3, Δу = 0,01.
Воспользуемся формулой (44.7), предварительно
найдя![]() Следовательно,
Следовательно,![]()
Для сравнения: используя микрокалькулятор, находим: 1,023,01 ≈ 1,061418168.
Отметим, что с помощью полного дифференциала можно найти: границы абсолютной и относительной погрешностей в приближенных вычислениях; приближенное значение полного приращения функции и т. д.
44.5. Дифференциалы высших порядков
Введем понятие дифференциала высшего порядка. Полный дифференциал функции (формула (44.5)) называют также дифференциалом первого порядка.
Пусть функция z=ƒ(х;у) имеет непрерывные частные производные второго порядка. Дифференциал второго порядка определяется по формуле (d2z = d(dz). Найдем его:

Отсюда:![]() Символически
это записывается так:
Символически
это записывается так:

Аналогично можно получить формулу для дифференциала третьего порядка:

где

Методом математической индукции можно показать, что

Отметим, что полученные формулы справедливы лишь в случае, когда переменные х и у функции z = ƒ(х;у) являются независимыми.
Пример 44.4. (Для самостоятельного решения.) Найти d2z, если z=х3у2.
Ответ: d2z=бху2dx2+12х2уdxdy+2х3dy2.
44.6. Производная сложной функции. Полная производная
Пусть z=ƒ(х;у) — функция двух переменных х и у, каждая из которых является функцией независимой переменной t: х = x(t), у = y(t). В этом случае функция z = f(x(t);y(t)) является сложной функцией одной независимой переменной t; переменные х и у — промежуточные переменные.
Теорема 44.4. Если z = ƒ(х;у) — дифференцируемая в точке М(х;у) є D функция и х = x(t) и у = y(t) — дифференцируемые функции независимой переменной t, то производная сложной функции z(t) = f(x(t);y(t)) вычисляется по формуле
![]()
Дадим независимой переменной t приращение Δt. Тогда функции х = = x(t) и у = y{t) получат приращения Δх и Δу соответственно. Они, в свою очередь, вызовут приращение Az функции z.
Так как по условию функция z — ƒ(х;у) дифференцируема в точке М(х; у), то ее полное приращение можно представить в виде
![]()
где а→0, β→0 при Δх→0, Δу→0 (см. п. 44.3). Разделим выражение Δz на Δt и перейдем к пределу при Δt→0. Тогда Δх→0 и Δу→0 в силу непрерывности функций х = x(t) и у = y(t) (по условию теоремы — они дифференцируемые). Получаем:

т. е.

или

Частный случай: z=ƒ(х;у), где у=у(х), т. е. z=ƒ(х;у(х)) — сложная функция одной независимой переменной х. Этот случай сводится к предыдущему, причем роль переменной t играет х. Согласно формуле (44.8) имеем:

Формула (44.9) носит название формулы полной производной.
Общий
случай: z=ƒ(х;у), где x=x(u;v), у=у(u;v). Тогда z=
f(x(u;v);y(u;v)) — сложная функция независимых
переменных u и v. Ее частные производные![]() можно
найти, используя формулу (44.8) следующим
образом. Зафиксировав v, заменяем в
ней
можно
найти, используя формулу (44.8) следующим
образом. Зафиксировав v, заменяем в
ней![]() соответствующими
частными производными
соответствующими
частными производными![]()

Аналогично
получаем:![]()
Таким образом, производная сложной функции (z) по каждой независимой переменной (u и v) равна сумме произведений частных производных этой функции (z) по ее промежуточным переменным (х и у) на их производные по соответствующей независимой переменной (u и v).
Пример
44.5. Найти![]() если
z=ln(x2+у2),
х=u•v, у=u/v.
если
z=ln(x2+у2),
х=u•v, у=u/v.
Решение: Найдем dz/du (dz/dv — самостоятельно), используя формулу (44.10):

Упростим правую часть полученного равенства:

т.
е.![]()
44.7. Инвариантность формы полного дифференциала
Используя правило дифференцирования сложной функции, можно показать, что полный дифференциал обладает свойством инвариантности: полный дифференциал функции z=ƒ(х;у) сохраняет один и тот же вид независимо от того, являются ли аргументы независимыми переменными или функциями независимых переменных.
Пусть z=ƒ(х;у), где х и у — независимые переменные. Тогда полный дифференциал (1-го порядка) функции имеет вид
![]() (формула
(44.5)).
(формула
(44.5)).
Рассмотрим сложную функцию z=ƒ(х;у), где х = x(u;v), у = y(u;v), т. е. функцию z = f(x(u;v);y(u;v)) = F(u;v;), где u и v — независимые переменные. Тогда имеем:

Выражения в скобках представляют собой полные дифференциалы dx и dy функций х = х(u;v) и y = y(u;v). Следовательно, и в этом случае,

44.8. Дифференцирование неявной функции
Функция z = ƒ (х; у) называется неявной, если она задается уравнением
![]()
неразрешенным
относительно z. Найдем частные
производные ![]() неявной
функции z, заданной уравнением (44.11). Для
этого, подставив в уравнение вместо z
функцию ƒ (х; у), получим тождество F(x;у;ƒ
(х; у)) = 0. Частные производные по х и по
у функции, тождественно равной нулю,
также равны нулю:
неявной
функции z, заданной уравнением (44.11). Для
этого, подставив в уравнение вместо z
функцию ƒ (х; у), получим тождество F(x;у;ƒ
(х; у)) = 0. Частные производные по х и по
у функции, тождественно равной нулю,
также равны нулю:

откуда

Замечания.
а)
Уравнение вида (44.11) не всегда определяет
одну переменную как неявную функцию
двух других. Так, уравнение х2+у2+z2-4=0
определяет функции![]() определенные
в круге х2+у2≤4,
определенные
в круге х2+у2≤4,![]() определенную
в полукруге х2+у2 ≤ 4 при у≥ 0 и т. д., а
уравнение cos(x + 2у +3z)- 4 = 0 не определяет
никакой функции.
определенную
в полукруге х2+у2 ≤ 4 при у≥ 0 и т. д., а
уравнение cos(x + 2у +3z)- 4 = 0 не определяет
никакой функции.
Имеет место теорема существования неявной функции двух переменных: если функция F(x; у; z) и ее производные F'x(x; у; z), F'y(x; у; z), F'z(x;y;z) определены и непрерывны в некоторой окрестности точки M0(x0;y0;z0), причем F(x0;y0;z0)=0, а F'z(x0;y0;z0)≠0, то существует окрестность точки М0, в которой уравнение (44.11) определяет единственную функцию z=ƒ(х;у), непрерывную и дифференцируемую в окрестности точки (х0;у0) и такую, что ƒ(х0;у0)=z0.
б) Неявная функция у=ƒ(х) одной переменной задается уравнением F(x;у)=0. Можно показать, что в случае, если удовлетворены условия существования неявной функции одной переменной (имеется теорема, аналогичная вышеуказанной), то производная неявной функции находится по формуле

Пример 44.6. Найти частные производные функции z, заданной уравнением ez+z-х2у+1=0.
Решение: Здесь F(x;y;z)=ez+z-х2у+1, F'x=-2ху, F'y = -х2, F'z=ez+1. По формулам (44.12) имеем:
![]()
Пример
44.7. Найти ![]() если
неявная функция у=ƒ(х) задана уравнением
у3+2у=2х.
если
неявная функция у=ƒ(х) задана уравнением
у3+2у=2х.
Решение: Здесь F(x;у) = у3+2у-2х, F'x=-2, F'y = 3у2+2. Следовательно,
![]()
46.1. Основные понятия
Понятие максимума, минимума, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной независимой переменной (см. п. 25.4).
Пусть функция z = ƒ(х;у) определена в некоторой области D, точка N(x0;y0) D.
Точка (х0;у0) называется точкой максимума функции z=ƒ(х;у), если существует такая -окрестность точки (х0;у0), что для каждой точки (х;у), отличной от (хо;уо), из этой окрестности выполняется неравенство ƒ(х;у)<ƒ(хо;уо).
А налогично
определяется точка минимума функции:
для всех точек (х; у), отличных от (х0;у0),
из -окрестности точки (хо;уо)
выполняется неравенство: ƒ(х;у)>ƒ(х0;у0).
налогично
определяется точка минимума функции:
для всех точек (х; у), отличных от (х0;у0),
из -окрестности точки (хо;уо)
выполняется неравенство: ƒ(х;у)>ƒ(х0;у0).
На рисунке 210: N1 — точка максимума, а N2 — точка минимума функции z=ƒ(x;у).
Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум и минимум функции называют ее экстремумами.
Отметим, что, в силу определения, точка экстремума функции лежит внутри области определения функции; максимум и минимум имеют локальный (местный) характер: значение функции в точке (х0;у0) сравнивается с ее значениями в точках, достаточно близких к (х0; у0). В области D функция может иметь несколько экстремумов или не иметь ни одного.
46.2. Необходимые и достаточные условия экстремума
Рассмотрим условия существования экстремума функции.
Теорема 46.1 (необходимые условия экстремума). Если в точке N(x0;y0) дифференцируемая функция z=ƒ(х;у) имеет экстремум, то ее частные производные в этой точке равны нулю: ƒ'x(х0;у0)=0, ƒ'y(х0;у0)=0.
Зафиксируем одну из переменных. Положим, например, у=у0. Тогда получим функцию ƒ(х;у0)=φ(х) одной переменной, которая имеет экстремум при х = х0. Следовательно, согласно необходимому условию экстремума функции одной переменной (см. п. 25.4), φ'(х0) = 0, т. е. ƒ'x(х0;y0)=0.
Аналогично можно показать, что ƒ'y(х0;у0) = 0.
Геометрически равенства ƒ'x(х0;у0)=0 и ƒ'y(х0;у0)=0 означают, что в точке экстремума функции z=ƒ(х;у) касательная плоскость к поверхности, изображающей функцию ƒ(х;у), параллельна плоскости Оху, т. к. уравнение касательной плоскости есть z=z0 (см. формулу (45.2)).
З амечание.
Функция может иметь экстремум в точках,
где хотя бы одна из частных производных
не существует. Например, функция
амечание.
Функция может иметь экстремум в точках,
где хотя бы одна из частных производных
не существует. Например, функция![]() имеет
максимум в точке О(0;0) (см. рис. 211), но не
имеет в этой точке частных производных.
имеет
максимум в точке О(0;0) (см. рис. 211), но не
имеет в этой точке частных производных.
Точка, в которой частные производные первого порядка функции z ≈ ƒ(х; у) равны нулю, т. е. f'x=0, f'y=0, называется стационарной точкойфунк ции z.
Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками.
В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Рассмотрим, например, функцию z = ху. Для нее точка О(0; 0) является критической (в ней z'x=у и z'y — х обращаются в ноль). Однако экстремума в ней функция z=ху не имеет, т. к. в достаточно малой окрестности точки О(0; 0) найдутся точки для которых z>0 (точки I и III четвертей) и z < 0 (точки II и IV четвертей).
Таким образом, для нахождения экстремумов функции в данной области необходимо каждую критическую точку функции подвергнуть дополнительному исследованию.
Теорема 46.2 (достаточное условие экстремума). Пусть в стационарной точке (хо;уо) и некоторой ее окрестности функция ƒ(х;у) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке (х0;у0) значения A=f''xx(x0;y0), В=ƒ''xy(х0;у0), С=ƒ''уy(х0;у0). Обозначим

Тогда:
1. если Δ > 0, то функция ƒ(х;у) в точке (х0;у0) имеет экстремум: максимум, если А < 0; минимум, если А > 0;
2. если Δ < 0, то функция ƒ(х;у) в точке (х0;у0) экстремума не имеет.
В случае Δ = 0 экстремум в точке (х0;у0) может быть, может не быть. Необходимы дополнительные исследования.
Примем без доказательства.
Пример 46.1. Найти экстремум функции z = 3х2у- х3 - у4.
Решение: Здесь z'x=бху-3х2, z'y=3х2-4у3. Точки, в которых частные производные не существуют, отсутствуют.
Найдем стационарные точки, решая систему уравнений:

Отсюда получаем точки M1(6;3) и М2(0;0).
Находим частные производные второго порядка данной функции: z''xх=6у-6х, z''xу=6х, z''уy=-12у2.
В точке М1(6;3) имеем: А = -18, В = 36, С = -108, отсюда
АС-В2=-18•(-108)-362=648, т. е. Δ>0.
Так как А<0, то в точке М1 функция имеет локальный максимум: zmax=z(6;3)=3•36•3-63-34=324-216-81=27.
В точке М2(0;0): А =0, В = 0, С = 0 и, значит, Δ = 0. Проведем дополнительное исследование. Значение функции z в точке М2 равно нулю: z(0;0)=0. Можно заметить, что z=-у4<0 при х=0, у ≠ 0; z =-х3>0 при х<0, у=0. Значит, в окрестности точки М2(0;0) функция z принимает как отрицательные, так и положительные значения. Следовательно, в точке М2 функция экстремума не имеет.
46.3. Наибольшее и наименьшее значения функции в замкнутой области
Пусть функция z=ƒ(х;у) определена и непрерывна в ограниченной замкнутой области D. Тогда она достигает в некоторых точках D своего наибольшего М и наименьшего т значений (т. н. глобальный экстремум). Эти значения достигаются функцией в точках, расположенных внутри области D , или в точках, лежащих на границе области.
Правило нахождения наибольшего и наименьшего значений дифференцируемой в области D функции z = ƒ(х;у) состоит в следующем:
1. Найти все критические точки функции, принадлежащие D , и вычислить значения функции в них;
2. Найти наибольшее и наименьшее значения функции z = ƒ(х;у) на границах области;
3. Сравнить все найденные значения функции и выбрать из них наибольшее М и наименьшее т.
Пр имер
46.2. Найти наибольшее и наименьшее
значения функции z=х2у
+ ху2 +
ху в замкнутой области, ограниченной
линиями: у = 1/x,
х = 1, х = 2, у = -1,5 (см. рис. 212).
имер
46.2. Найти наибольшее и наименьшее
значения функции z=х2у
+ ху2 +
ху в замкнутой области, ограниченной
линиями: у = 1/x,
х = 1, х = 2, у = -1,5 (см. рис. 212).
Решение: Здесь z'x=2ху+у2+у, z'y=х2+2ху+х.
Находим все критические точки:
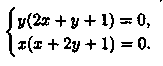
Решением системы являются точки (0;0), (-1;0), (0; -1),(-1/3;-1/3). Ни одна из найденных точек не принадлежит области D .
Исследуем функцию z на границе области, состоящей из участков АВ, ВС, СЕ и ЕА (рис. 212). На участке АВ:

 Значения
функции z(-1) = -1,
Значения
функции z(-1) = -1,
 На
участке ВС:
На
участке ВС:
 Значения
функции z(1) = 3, z(2) = 3,5.
На участке
СЕ:
Значения
функции z(1) = 3, z(2) = 3,5.
На участке
СЕ: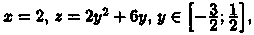 z'y=4у+6,
4у+6=0, у=-3/2.
Значения функции
z'y=4у+6,
4у+6=0, у=-3/2.
Значения функции
 На
участке АЕ:
На
участке АЕ:
 Значения
функции z(1) = -3/4,z(2) = -4,5.
Значения
функции z(1) = -3/4,z(2) = -4,5.Сравнивая полученные результаты, имеем: М = +3,5 = z(2;1/2) =z(С); а m=-4,5=z(2;-3/2)=z(E).
Глава 1. Числовые ряды |
|
§1. Определение ряда и его сходимость |
Определение 1. Пусть задана бесконечная числовая последовательность u1, u2,…,un,…. Выражение
называется числовым рядом. Числа u1, u2,…,un,… называются первым, вторым, …, n-м, … членами ряда. un также называется общим членом ряда. Определение 2. Сумма конечного числа n первых членов ряда называется n-ой частичной суммой ряда:
Определение
3. Если
существует конечный предел |
§2. Простейшие свойства числовых рядов |
Теорема 1. Если сходится ряд, полученный из ряда (1) отбрасыванием нескольких его членов, то сходится и ряд (1). Обратно, если сходится данный ряд (1), то сходится ряд, полученный из ряда (1) отбрасыванием нескольких членов. Другими словами: на сходимость ряда не влияет отбрасывание конечного числа его членов. Доказательство. Пусть Sn – n-я частичная сумма ряда (1), Ck – сумма к отброшенных членов (заметим, что при достаточно большом n все отброшенные члены содержатся в сумме Sn),n-k – сумма членов ряда, входящих в сумму Sn и не входящих в Ck. Таким образом:
где Ck – постоянное число, не зависящее от n.
Из
последнего равенства следует, что
если существует
Теорема 2. Если ряд (1) сходится и его сумма равна S, то ряд
где с – число, также сходится и его сумма равна c.S. Доказательство. Пусть Sn и n – n-е частичные суммы соответственно рядов (1) и (2). Тогда
Предел n существует, так как
Теорема 3. Если ряды
и
сходятся
и их суммы равны соответственно
и
(u1-v1)+
(u2-v2)+…+
(un-vn)+…
также
сходятся и их суммы равны
соответственно
Доказательство.
Докажем сходимость ряда (4).
Обозначим n, n=(u1+v1)+(u2+v2)+…+(un+vn)=(u1+u2+…+un)+ +(v1+v2+…+vn)= + Sn. Переходя в этом равенстве к пределу при n, получим
= Таким образом, ряд (4) сходится и его сумма равна + S. Аналогично доказывается, что ряд (5) сходится и его сумма равна -S. Сделайте это самостоятельно. |
§3. Необходимый признак сходимости ряда |
Теорема. Если ряд сходится, то un=0.
Доказательство.
Пусть ряд u1+u2+…+un… сходится, то
есть существует конечный предел
Следствие. Если Пример.
Ряд
un= Подчеркнём, что рассмотренный признак является только необходимым, но не достаточным, то есть из того, что un=0 не следует, что ряд сходится. Позже докажем, что так называемый гармонический ряд
расходится,
хотя
un= Этот ряд часто будет использоваться в дальнейшем. |
§4. Достаточные признаки сходимости знакоположительных числовых рядов |
Определение 4. Числовой ряд называется знакоположительным, если un>0 при всех n=1,2,3… . Нахождение суммы ряда S= часто связано с большими техническими трудностями. В таких случаях сумму находят приближённо: S≈Sn. Последнее равенство тем точнее, чем большеn, при условии, что ряд сходится. Сходимость или расходимость ряда во многих случаях можно установить с помощью достаточных признаков сходимости числовых рядов. В этом параграфе будем рассматривать знакоположительные числовые ряды. Для таких рядов частичные суммы S1, S2, …,Sn,… образуют возрастающую числовую последовательность S1<S2<…<Sn<… . Возможны два случая: 1) последовательность частичных сумм неограничена; в этом случае =∞ и ряд расходится; 2) последовательность частичных сумм ограничена, то есть существует такое число С>0, что Sn<C при любых n=1,2,… . В этом случае существует конечный предел , следовательно, ряд сходится. Таким образом, для доказательства сходимости знакоположительного числового ряда достаточно доказать ограниченность последовательности его частичных сумм.
Теорема 4. (Признак сравнения) Пусть даны два знакоположительных числовых ряда
причём un≤vn при любых n=1,2,… . Тогда: 1. Если ряд (8) сходится, то сходится и ряд (7); 2. Если ряд (7) расходится, то расходится и ряд (8).
Доказательство.
Обозначим n-е частичные суммы рядов
(7) и (8) через Sn и sn соответственно.
Пусть ряд (8) сходится. Это значит, что
существует конечный
Замечания. 1. В силу теоремы 1 признак сравнения справедлив и в случае, если un≤vn начиная с некоторого номера к, то есть при n≥k.
2. Для
использования признака сравнения
нужно иметь для сравнения ряды, про
которые заранее известно, сходятся
они или расходятся. В качестве таких
рядов можно использовать сходящуюся
бесконечно убывающую геометрическую
прогрессию, а также обобщённые
гармонические ряды
Пример Исследовать на сходимость ряд
Рассмотрим
расходящийся ряд
Он
расходится, так как получен из
гармонического ряда отбрасыванием u1=1.
Так как ln(n+1)<n+1 при любом n=1,2,…,
то
Теорема 5. (Предельный признак сравнения)
Пусть
даны два знакоположительных числовых
ряда (7) и (8). Если существует конечный
предел
Доказательство. По
условию теоремы существует конечный
предел
.
Это означает, что для любого положительного
числа Е существует такой номер N,
что для всех номеровn≥N выполняется
условие
Неравенство
(9) верно при любом E>0. Выберем
поэтому Е так, чтобы выполнялось А-Е>0.
Если ряд (8) сходится, то сходится и
ряд
Замечание. Предельный признак сравнения рекомендуется применять в тех случаях, когда общий член ряда представляет собой отношение степенных функций. Для сравнения выбирается обобщённый гармонический ряд, общий член которого равен отношению старших степеней числителя и знаменателя общего члена данного ряда.
Пример.
Исследовать
на сходимость ряд
Возьмём
для сравнения ряд с общим членом vn=
следовательно, данный ряд расходится по предельному признаку сравнения.
Теорема 6. (Признак Даламбера) Пусть дан знакоположительный числовой ряд
и
пусть существует предел
Доказательство.
По условию существует предел
p-E<
Пусть
сначала p<1. Выберем Е так,
что p+E=q<1. Для всех n³N имеем
или
Рассмотрим ряды
Ряд (13) сходится, так как он является бесконечно убывающей геометрической прогрессией. Тогда ряд (12) сходится, учитывая (11), по признаку сравнения. Ряд (7) сходится по теореме 1.
Пусть
теперь p>1. Выберем Е так,
что p-E>1. Тогда из левой части
неравенства (10) следует, что
при n³N выполняется
Замечания. 1. Если расходимость ряда установлена с помощью признака Даламбера, то un¹0. 2. При р=1 признак Даламбера не даёт ответа о сходимости ряда. В этом случае нужно применять другие признаки сходимости. 3. Признак Даламбера рекомендуется применять при наличии в выражении общего члена ряда показательной функции или факториала. Пример.
Исследовать
на сходимость ряд
Применим
признак Даламбера. un=
Теорема 7. (Признак Коши) Пусть дан знакоположительный числовой ряд u1+u2+…+un… (7)
и
пусть существует предел
Доказательство.
По условию существует
Это
означает, что для любого положительного
числа Е существует такой номер N,
что для всех n³N выполняется
условие |
p-E< Пусть p<1. Выберем Е таким, чтобы выполнялось p+E=q<1. Тогда из (14) получаем <q или un<qn для всех n³N. Рассмотрим ряды
Ряд (16) сходится, так как он является бесконечно убывающей геометрической прогрессией. Ряд (15) сходится, учитывая, что un<qn для всех n³N, по признаку сравнения, следовательно, по теореме 1 сходится ряд (7). Пусть теперь p>1. Выберем Е так, чтобы выполнялось условие p-E >1. Тогда из (14) получаем >1 или un>1, следовательно, un¹0 и ряд (7) расходится по следствию из необходимого признака сходимости. Теорема доказана.
Теорема 8. (Интегральный признак Коши)
Пусть
члены знакоположительного числового
ряда u1+u2+…+un… (7) не
возрастают: u1³u2≥…≥un≥… и
пусть f(x) такая положительная,
непрерывная, невозрастающая на
промежутке [1;∞) функция,
что f(1)=u1, f(2)= u2 ,…, f(n)=
=un,… . Тогда ряд (7) сходится или расходится
одновременно с несобственным
интегралом
Доказательство. Построим график функции y=f(x) на отрезке [1;n] и построим прямоугольник с основаниями [1;2], [2;3], …, [n-1;n] и высотами u1,u2,…,un-1, а также с высотами u2,u3,…,un. Sn=u1+u2+…+un-1+un, Sвпис=u2.1+u3.1+…+un.1=u2+u3+…+un=Sn-u1, Sопис=u1+u2+…+ +un-1=Sn-un.
Площадь
криволинейной трапеции S= Sn<u1+ (17) и Sn>un+ (18)
Пусть
Пример.
Исследуем
с помощью интегрального признака Коши
обобщённый гармонический ряд
Очевидно, f(x)=
При к=1
имеем Таким образом, обобщённый гармонический ряд сходится при k>1 и расходится при k≤1. |
§5. Знакопеременные ряды |
Определение 5. Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами. Ряды, все члены которых отрицательные числа, не представляют нового по сравнению со знакоположительными рядами, так как они получаются умножением знакоположительных рядов на –1. Изучение знакопеременных рядов начнём с частного случая – знакочередующихся рядов. Определение 6. Числовой ряд вида u1-u2+u3-u4+…+ +(-1)n-1.un+…, где un – модуль члена ряда, называется знакочередующимся числовым рядом.
Теорема 9. (Признак Лейбница) Если для знакочередующегося числового ряда
Выполняются два условия: Члены ряда убывают по модулю u1>u2>…>un>…,
то ряд (19) сходится, причём его сумма положительна и не превосходит первого члена ряда. Доказательство. Рассмотрим частичную сумму чётного числа членов ряда S2n=(u1-u2)+(u3-u4)+…+(u2n-1-u2n). По условию u1>u2>…>u2n-1>u2n, то есть все разности в скобках положительны, следовательно, S2n возрастает с возрастанием n и S2n>0 при любом n. С другой стороны S2n=u1-[(u2-u3)+(u4-u5)+…+(u2n-2-u2n-1)+u2n]. Выражение в квадратных скобках положительно и S2n>0, поэтому S2n<u1 для любого n. Таким образом, последовательность частичных сумм S2n возрастает и ограничена, следовательно, существует конечный S2n=S. При этом 0<S≤u1. Рассмотрим теперь частичную сумму нечётного числа членов ряда S2n+1=S2n+u2n+1. Перейдём в последнем равенстве к пределу при n→∞: S2n+1= S2n+ u2n+1=S+0=S. Таким образом, частичные суммы как чётного, так и нечётного числа членов ряда имеют один и тот же предел S, поэтому Sn=S, то есть данный ряд сходится. Теорема доказана.
Пример.
Исследовать
на сходимость ряд Применим признак Лейбница.
un=
un=
Оба условия признака Лейбница выполняются, следовательно, ряд сходится.
Замечания. 1. Теорема Лейбница справедлива и если условие un>un+1 выполняется, начиная с некоторого номера N.
2.
Условие un>un+1 не является
необходимым. Ряд может сходиться, если
оно не выполняется. Например,
ряд Определение 8. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин членов этого ряда, расходится, то говорят, что знакопеременный ряд сходится условно. Определение 9. Если сходится и сам знакопеременный ряд и ряд, составленный из абсолютных величин его членов, то говорят, что знакопеременный ряд сходится абсолютно. Пример.
Установить
характер сходимости ряда
Очевидно,
что данный ряд сходится по признаку
Лейбница. Действительно:
Ряд,
составленный из абсолютных величин
членов данного ряда
Теорема 10. (Достаточный признак сходимости знакопеременного ряда или признак абсолютной сходимости) Пусть
u1+u2+…+un+…= знакопеременный ряд и пусть сходится ряд, составленный из абсолютных величин его членов
│u1│+│ u2│+…+│ un │+…= Тогда ряд (20) тоже сходится. Доказательство. Рассмотрим вспомогательный ряд
(u1+│u1│)+(u2+│u2│)+…+(un+│un│)+…= Очевидно, 0≤ un+│un│≤2│un│ при всех n=1, 2, … . Ряд (21) сходится по условию, поэтому сходится ряд 2│un│, тогда по признаку сравнения сходится ряд (22). Ряд (20) представляет собой разность двух сходящихся рядов (22) и (21), поэтому он тоже сходится. Теорема доказана.
Замечание. Обратное утверждение неверно. Если данный ряд сходится, то ряд, составленный из абсолютных величин его членов, может и расходиться.
Например,
ряд
Остаток ряда и его оценка Рассмотрим сходящийся числовой ряд
Вычисление
суммы ряда S= Определение 7. Если числовой ряд сходится, то разность Rn=S-Sn называется n-м остатком ряда. Таким образом, Rn представляет собой сходящийся числовой ряд: Rn= un+1+un+2+… . Заметим, что Rn= ( S-Sn)=S-S=0. Абсолютная погрешность при замене суммы ряда S его частичной суммой Sn равна |Rn|=|S-Sn|. Таким образом, если требуется найти сумму ряда с точностью до E>0, то надо взять сумму такого числа n первых членов ряда, чтобы выполнялось условие |Rn|<E. Однако в общем случае находить точно Rn не удаётся.
Теорема 11. (Об оценке остатка знакочередующегося числового ряда) Если знакочередующийся числовой ряд сходится по признаку Лейбница, то его n-й остаток по абсолютной величине не превосходит модуля (n+1)-го члена ряда. Доказательство. Пусть ряд u1-u2+u3-u4+…+(-1)n-1.un+… сходится по признаку Лейбница. Тогда n-й остаток ряда Rn=±(un+1-un+2+un+3-…) сам является суммой знакочередующегося числового ряда и по теореме Лейбница |Rn|≤|un+1|. Теорема доказана.
Пример.
Вычислить
с точностью до 0,01 сумму ряда Очевидно,
ряд сходится по признаку
Лейбница. u1= |
Глава 2. Степенные ряды |
|
§6. Основные понятия |
Определение 10. Ряд, члены которого являются функциями, называется функциональным рядом. Его обозначают: u1(x)+u2(x)+…+un(x)+… . Определение 11. Если при x=x0 функциональный ряд сходится, то x0 называется точкой сходимости функционального ряда. Определение 12. Множество всех точек сходимости функционального ряда называется его областью сходимости. Очевидно, что в области сходимости функционального ряда его сумма является функцией от x. Будем обозначать её S(x). Определение 13. Степенным рядом называется функциональный ряд вида
где a, a0, a1, a2, …, an, … – некоторые числа, называемые коэффициентами степенного ряда.
Теорема 12. (О структуре области сходимости степенного ряда)
Областью
сходимости степенного ряда (24) является
интервал (a-R;a+R), к которому в
зависимости от конкретных случаев
могут быть присоединены точки a-R и a+R,
где R= Доказательство. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда: |a0|+|a1|.|x-a|+|a2|.|x-a|2+…+|an|.|x-a|n+… (25) Применим к ряду (25) признак Даламбера
Возможны три случая:
1.
Если
2.
Если Определение 14. Интервал (a-R;a+R), называется интервалом сходимости степенного ряда, а половина его длины R называется радиусом сходимости степенного ряда.
Замечание. Любой степенной ряд (24) сходится при x=a. Если других точек сходимости у ряда (24) нет, то считают, что R=0. Если степенной ряд (24) сходится во всех точках числовой прямой, то считают, что R=∞.
Примеры. Найти область сходимости степенного ряда.
1.
Составим
ряд из абсолютных величин членов
данного ряда
Ряд
сходится, если |x|<1 или x
Действительно,
=
2.
Составим
ряд из абсолютных величин членов
данного ряда
3.
Составим
ряд из абсолютных величин членов
данного ряда
Свойства степенных рядов Отметим здесь без доказательства три важных свойства степенных рядов: 1. Сумма S(x) степенного ряда S(x)=a0+a1(x-a)+a2(x-a)2+…+an(x-a)n+… (24) является непрерывной функцией в каждой точке интервала сходимости (a-R;a+R). 2. Ряд φ(x)=a1+2a2(x-a)+…+nan(x-a)n-1+…, (26) полученный почленным дифференцированием ряда (24), является степенным рядом с тем же, что и ряд (24), интервалом сходимости (a-R;a+R). Сумма ряда (26) φ(x)=S'(x).
Замечание.
Ряд (26) также можно почленно
дифференцировать и сумма полученного
после этого ряда равна
3.
Пусть числа
|
§7. Разложение функций в степенные ряды |
Пусть функция f(x) бесконечно дифференцируема в (a-R;a+R) и является суммой степенного ряда f(x)= a0+a1(x-a)+a2(x-a)2+…+an(x-a)n+…, (27) где (a-R;a+R) – интервал сходимости ряда (27). В этом случае говорят, что функция f(x) разлагается в степенной ряд в окрестности точки а или по степеням (x-a). Определим коэффициентыa0, a1, a2, …, an,… ряда (27), для чего продифференцируем n раз ряд (27). f(x)=a0+a1(x-a)+a2(x-a)2+ a3(x-a)3+ a4(x-a)4+…+an(x-a)n+… f’(x)=a1+2a2(x-a)+3a3(x-a)2+ 4a4(x-a)3+…+nan(x-a)n-1+… f′′(x)=2a2+3.2a3(x-a)+4.3a4(x-a)2+…+(n-1)nan(x-a)n-2+… f′′′(x)=3.2a3+4.3.2a4(x-a)+…+(n-2)(n-1)nan(x-a)n-3+… ………………………………………… f(n)(x)=2.3…(n-2)(n-1)nan+… …………………………………………
Все
ряды имеют интервал сходимости
(a-R;a+R). При x=a из полученных тождеств
получаем f(a)=a0, f’(a)=a1, f’’(a)=2a2,
…, f(n)(a)= 2.3…(n-2)(n-1)nan, … . Отсюда находим
коэффициенты степенного ряда
(27): a0=f(a), a1=
f(x)=f(a)+ ряд (28) называется рядом Тейлора для функции f(x) в точке a. В частном случае при a=0 ряд (28) принимает вид
f(x)=f(0)+ и называется рядом Маклорена. Таким образом, если функция f(x) является суммой степенного ряда, то этот ряд называется рядом Тейлора для функции f(x). Пусть теперь дана бесконечно дифференцируемая в точке a функция f(x). Составим для неё формально ряд Тейлора:
f(a)+ Совпадает ли сумма полученного ряда Тейлора с функцией f(x), для которой он составлен? Оказывается, не всегда. При каких условиях сумма ряда Тейлора совпадает с функцией, для которой он составлен? Рассмотрим n-ю частичную сумму ряда Тейлора Sn(x)= f(a)+ +…+ . (30) Многочлен (30) называется многочленом Тейлора степени n. Разность Rn(x)=f(x)-Sn(x) называется остаточным членом ряда Тейлора. Приведём без доказательства следующую теорему.
Теорема 13. Для того, чтобы бесконечно дифференцируемая в точке а функция f(x) являлась суммой составленного для неё ряда Тейлора, необходимо и достаточно, чтобы Rn(x)=0.
Можно
показать, что остаточный член можно
представить в форме Лагранжа: Rn(x)=
f(x)= f(a)+
+…+
+ Формула (31) называется формулой Тейлора, а её частный случай при а=0 называется формулой Маклорена: f(x)= f(0)+ |
|
|
§8. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена |
1. Разложение функции f(x)=ex в ряд Маклорена. f(x)=f′(x)=f″(x)=…=f(n)(x)=…=ex. f(0)=f′(0)=f″(0)=…=f(n)(0)=…=1.
Составим
для функции f(x)=ex формально ряд
Маклорена: 1+ Найдём области сходимости этого ряда.
ex=1+ . (32) 2. Разложение функции f(x)=sinx в ряд Маклорена. Вычислим производные данной функции.
f′(x)=cosx=sin(x+
f″′(x)=-cosx=sin(x+ Исследуем остаточный член ряда.
|Rn(x)|=
=
sinx=x- 3. Разложение функции y=cosx в ряд Маклорена. Дифференцируя ряд (33), получаем разложение при x (-∞;+∞):
cosx=1- 4. Биномиальный ряд. Разложим в ряд Маклорена функцию f(x)=(1+x)m, где m≠0 – любое действительное число. Для этого вычислим производные: f′(x)=m(1+x)m-1, f″(x)=(m-1)m(1+x)m-2, f″′(x)=(m-2)(m-1)m(1+x)m-3, …, f(n)(x)=(m-n+1)…(m-2).(m-1)m(1+x)m-n, … При x=0 получаем f(0)=1, f′(0)=m, f″(0)=(m-1)m, f″′(0)=(m--2)(m-1)m, …, f(n)(0)=(m-n+1)…(m-2)(m-1)m, … . Можно показать, что областью сходимости ряда является промежуток (-1;1) (на концах интервала ряд сходится или расходится в зависимости от конкретных значений m) и что . Таким образом, при x (-1;1) имеет место разложение:
(1+x)m=1+
+…+ Ряд (35) называется биномиальным рядом. 5. Разложение функции f(x)=lnx в ряд Тейлора. При x=0 функция f(x)=lnx не определена, поэтому её нельзя разложить в ряд Маклорена. Разложим её в ряд Тейлора, например, по степеням (x-1). Для этого, вычислим производные: f′(x)=x-1, f″(x)=-1.x-2=-1!x-2, f″′(x)=1.2.x-3=2!x-3, f(4)(x)=-1.2. .3.x-4=-3!x-4, …, f(n)(x)=(-1)n-1. .(n-1)!x-n, … . При x=1 получаем: f(1)=0, f′(1)=1, f″(1)=-1!, f″′(1)=2!, f(4)(1)=-3!, …, f(n)(1)=(-1)n-1(n-1)!, … .
Можно
показать, что областью сходимости
ряда является промежуток (0;2] и что
lnx= Заметим, что разложение функций в ряды Тейлора или Маклорена непосредственно часто связано с громоздкими вычислениями при нахождении производных и исследовании остаточного члена. На примерах покажем некоторые приёмы, позволяющие избежать этих трудностей.
Примеры.
1.
Разложить в степенной ряд функцию В формуле (32) сделаем замену переменной x=-t2, получим
2.
Разложить в степенной ряд функцию f(x)=
Очевидно, f(x)=
=1-t+t2-t3+…+(-1)n.tn+… , t (-1;1). (37) Возвращаясь к переменной x, получаем разложение при x (-1;1): =1-x2+x4-x6+…+(-1)n.x2n+… . (38) 3. Разложить в ряд Маклорена функцию f(x)=ln(1+x). Проинтегрируем обе части равенства (37) от 0 до x при x (-1;1). Получим
или
ln(1+x)=x Можно показать, что ряд (39) имеет область сходимости (-1;1]. 4. Разложить в степенной ряд функцию f(x)=arctgx. Проинтегрируем обе части равенства (38) от 0 до x при x (-1;1):
или
arctgx=x Можно показать, что ряд (40) имеет область сходимости [-1;1]. |
§9. Применение рядов к приближённым вычислениям |
Числовые и функциональные ряды широко применяются в приближённых вычислениях. Рассмотрим это на примерах.
Пример 1.
Вычислить
Воспользуемся
разложением
= Так как ряд знакочередующийся и 0,0008<0,001, то все слагаемые, начиная с 0,0008, отбрасываем и при этом погрешность не превосходит 0,001.
Пример 2.
Вычислить
=
≈2(1+
+ Так как, начиная со второго члена, ряд знакочередующийся и 0,00096<0,001, то все слагаемые, начиная с 0,00096, отбрасываем и при этом погрешность не превосходит 0,001.
Пример 3. Вычислить e0,1 с точностью до 0,001.
Для
функции ex формула Тейлора имеет
вид: ex=1+x+
При x=0.1
получаем знакоположительный числовой
ряд. Так как при этом с При x=0,1 получаем
e0,1≈1+0,1+ Так как 0,0002<0,0005, то достаточно взять четыре члена ряда.
Пример 4. Проинтегрировать дифференциальное уравнение y′=y+x2, y(0)=-2 методом последовательного дифференцирования. Будем искать решение в виде ряда Маклорена:
y(x)=y(0)+ Вычислим производные: y′=y+x2, y″=y′+2x, y″′=y″+2, y(4)= y″′, …, y(n)= y″′ при n=4, 5, … . При x=0 получаем: y(0)=-2, y′(0)=-2, y″(0)=-2, y(n)(0)=0 при n=3, 4, 5. Окончательно получаем y(x)=-2-2x-x2. |

 .
. ¹0,
¹0, следовательно,
ряд сходится по признаку Даламбера.
следовательно,
ряд сходится по признаку Даламбера.

 |x|.
|x|. так
как |sin(c+(n+1)
|≤1.
Переходя к пределу
при n→∞, получаем
так
как |sin(c+(n+1)
|≤1.
Переходя к пределу
при n→∞, получаем 
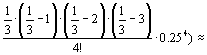 2.(1+0,0833--0,0069+0,00096)
≈
≈2.(1+0,0833-0,0069) ≈2,1528≈2,153.
2.(1+0,0833--0,0069+0,00096)
≈
≈2.(1+0,0833-0,0069) ≈2,1528≈2,153.