ВОПРОСЫ К ЭКЗАМЕНУ ПО ДИСЦИПЛИНЕ «ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»

1. Предмет теории вероятностей.

Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях.

Наблюдаемые нами события (явления) можно подразделить на следующие три вида: достоверные, невозможные и случайные. Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий S . Например, если в сосуде содержится вода при нормальном атмосферном давлении и температуре 20°С, то событие «вода в сосуде находится в жидком состоянии» есть достоверное. В этом примере заданные атмосферное давление и температура воды составляют совокупность условий ,S . Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена совокупность условий S. Например, событие «вода в сосуде находится в твердом состоянии» заведомо не произойдет, если будет осуществлена совокупность условий предыдущего примера. Случайным называют событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти. Например, если брошена монета, то она может упасть так, что сверху будет либо герб, либо надпись. Поэтому событие «при бросании монеты выпал герб» — случайное. Каждое случайное событие, в частности выпадение герба, есть следствие действия очень многих случайных причин (в нашем примере: силы, с которой брошена монета, формы монеты и многих других).

2. Случайные события .Действия над событиями.

Случайным событием (или просто событием) называется всякое явление, которое может произойти или не произойти при осуществлении определенной совокупности условий.

 Событие называется достоверным, если оно в данном опыте обязательно должно произойти; наоборот, событие называетсяневозможным, если оно в данном опыте не может произойти. Совмещением (или произведением) двух событий A и В называется событие, состоящее в совместном наступлении как события A, так и события В. Это событие будем обозначать АВ или ВА.  Аналогично, совмещением нескольких событий, например A, В и С, называется событие D=ABC, состоящее в совместном наступлении событий A, В и С. 

 Объединением (или суммой) двух событий A и В называется событие С, заключающееся в том, что произойдет по крайней мере одно из событий A или В. Это событие обозначается так: С=А+В.     Два события A и В называются несовместными, если наступление события A исключает наступление события В. Отсюда следует, что если события A и В несовместны, то событие AB — невозможное

3. Частота события, ее свойства

Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. Т.о., относительная частота события А определяется по формуле w(a)=m/n где m – число появлений события А, n – общее число испытаний.

Относительная частота обладает следующими свойствами:

1)  .

2)  .

3) Если   попарно несовместны, то 

Относительная частота обладает статистической устойчивостью (при большом числе испытаний её значения к одному и тому же числу).

Вывод: из свойства статистической устойчивости: существует доопытная характеристика (в каждом эксперименте) возможности события А, значение которой не зависит от проведения серии испытаний, а обусловлено самим комплексом условий. Доопытную характеристику события А называют вероятностью.

4. Вероятность события. Аксиомы теории вероятностей.

Вероятность события количественно характеризует возможность (шанс) осуществления этого события в ходе случайного эксперимента.

Пусть A и B — два несовместных события, причем в n испытаниях событие A произошло m1 раз, а событие В произошло m2 раз. Тогда частоты событий A и В соответственно равны P*(A)=m1/n, P*(B)=m2/n. Так как события A и В несовместны, то событие A+B в данной серии опытов произошло m1+m2 раз. Следовательно,

   Таким образом, частота события A+B равна сумме частот событий A и В. Но при больших n частоты P*(A), P*(B) и P*(A+B) мало отличаются от соответствующих вероятностей P(A), P(B) и P(A+B). Поэтому естественно принять, что если A и В — несовместные события, то P(A+B)=P(A)+P(B)     Изложенное позволяет высказать следующие свойства вероятностей, которые мы принимаем в качестве аксиом.     Аксиома 1. Каждому случайному событию A соответствует определенное число Р(А), называемое его вероятностью и удовлетворяющее условию  .     Аксиома 2. Вероятность достоверного события равна единице.     Аксиома 3 (аксиома сложения вероятностей). Пусть A и В — несовместные события. Тогда вероятность того, что произойдет хотя бы одно из этих двух событий, равна сумме их вероятностей:

P(A+B)=P(A)+P(B)

(1)

   Аксиома 3 допускает обобщение на случай нескольких событий, а именно: если события A1, A2, ..., An, попарно несовместны, то

5. Вычисление вероятности события.

6. Размещения, сочетания, перестановки.

пусть у нас есть множество из трех элементов  . Какими способами мы можем выбрать из этих элементов два?  .

Определение. Размещениями множества из   различных элементов по   элементов  называются комбинации, которые составлены из данных   элементов по   элементов и отличаются либо самими элементами, либо порядком элементов.

Число всех размещений множества из   элементов по   элементов обозначается через   (от начальной буквы французского слова “arrangement”, что означает размещение), где   и  .

Теорема. Число размещений множества из   элементов по   элементов равно

Доказательство. Пусть у нас есть элементы  . Пусть   — возможные размещения. Будем строить эти размещения последовательно. Сначала определим   — первый элемент размещения. Из данной совокупности   элементов его можно выбрать  различными способами. После выбора первого элемента   для второго элемента   остается   способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:

Пример. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?

Решение. Искомое число трехполосных флагов:

Определение. Перестановкой множества из   элементов называется расположение элементов в определенном порядке.

Так, все различные перестановки множества из трех элементов   — это

Очевидно, перестановки можно считать частным случаем размещений при  .

Число всех перестановок из   элементов обозначается   (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле

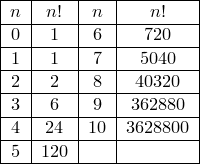
Пример. Сколькими способами можно расставить 8 ладей на шахматной доске так, чтобы они не били друг друга?

Решение. Искомое число расстановки 8 ладей

 по определению!

Определение. Сочетаниями из   различных элементов по   элементов называются комбинации, которые составлены из данных   элементов по   элементов и отличаются хотя бы одним элементом (иначе говоря,  -элементные подмножества данного множества из   элементов).

Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из   элементов по   элементов в каждом обозначается   (от начальной буквы французского слова “combinasion”, что значит “сочетание”).

Числа 

Все сочетания из множества   по два —  .

.

7. Алгебра событий.

Суммой А+В двух событий А и В называют событие, состоящее в том, что произошло хотя бы одно из событий А и В. Суммой нескольких событий, соответ-ственно, называется событие, заключающееся в том, что произошло хотя бы одно из этих событий.

Пример 1. Два стрелка делают по одному выстрелу по мишени. Если событие А – попадание первого стрелка, а событие В – второго, то сумма А+В – это хотя бы одно попадание при двух выстрелах.

Определение 1.2. Произведением АВ событий А и В называется событие, состоящее в том, что произошло и событие А, и событие В. Аналогично произведением нескольких событийназывается событие, заключающееся в том, что произошли все эти события.

Пример 3. В примере 1 ( два выстрела по мишени) событием АВ будет попадание обоих стрелков.

Определение 1.3. Разностью А\B событий А и В называется событие, состоящее в том, что А произошло, а В – нет.

Пример 5. Вернемся к примеру 1, где А\ В – попадание первого стрелка при промахе второго.

Определение 1.4. События А и В называются совместными, если они могут произойти оба в результате одного опыта. В противном случае (то есть если они не могут произойти одновременно) события называются несовместными.

Примеры: совместными событиями являются попадания двух стрелков в примере 1 и появление карты пиковой масти и дамы в примере 4; несовместными – события А₁ – А₆ в примере 2.

8. Статистическая вероятность. Классическая вероятность. Геометрическая вероятность.

Статистическая вероятность — относительная частота, с которой событие появляется внутри класса событий.

Вероятность классическая — вероятность   событий  , наступающих в результате исходов случайного эксперимента с конечным множеством равновероятных исходов Ω; определяется формулой

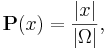
где | x | — мощность события x, число элементарных событий ω в x. Иначе говоря, классическая вероятность   события xопределяется как

«отношение числа | x | исходов, благоприятных x, к общему числу | Ω | исходов эксперимента».

Геометрическая вероятность события A, являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры Aк площади всего множества Ω:

9. Условная вероятность. Зависимые и независимые события.

Условная вероятность — вероятность одного события при условии, что другое событие уже произошло.

Независимыми называются события A и B, если вероятность события A не зависит от того, наступило событие B или нет. Например, при броске двух кубиков A₁ и B₅ – независимые события. Вероятность произведения независимых событий равна произведению соответствующих вероятностей. Вообще, равенство 

p (AiAk) = p(Ai) p(Ak)

является определением независимых событий.

Если вероятность наступления события A зависит от того, наступило событие B или нет, события называютзависимыми и вводят понятие условной вероятности. Условной вероятностью события A при условии того, что произошло событие B, называют величину 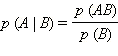  . Соответственно, для зависимых событийp (AB) = p (B) p (A | B).(см тетр )

10. Теорема умножения вероятностей и ее следствия.

(см тетр)

11. Теорема сложения вероятностей и ее следствия.(см тетр)

12. Формула полной вероятности.

Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез.

Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A, ..., HnA. Следовательно,

   Применяя аксиому сложения вероятностей, имеем

   Но   (i=1, 2, ..., n), поэтому

(11)

   Эта формула называется формулой полной вероятности. События H1, H2, ..., Hn часто называют «гипотезами». 

13. Формула Бейеса.(см тетр)

14. Схема Бернулли повторения независимых опытов(см тетр)

15. Дискретные и непрерывные случайные величины. См тетр

16. Ряд и многоугольник распределения.см тетр

17. Функция распределения и ее свойства. См тетр

18. Плотность распределения и ее свойства. См тетр

19. Числовые характеристики СВ и их назначение. См

20. Характеристики положения. Характеристики рассеивания. См

21. Понятие о моментах распределения. См

22. Биномиальное распределение. См

23. Распределение Пуассона. См

24. Равномерное распределение. См

25. Экспоненциальный закон распределения. См

26. Нормальный закон на прямой, его параметры. См

27. Функция Лапласа и ее свойства. См

28. Вероятность попадания нормально распределенной случайной величины на заданный интервал. См

29. Правило "3-х сигма" и "4E". См

30. Определение системы случайных величин. Таблица распределения. См

31. Функция распределения системы СВ и ее свойства. См

32. Плотность распределения системы СВ и ее свойства. См

33. Условные законы распределения. Зависимые и независимые СВ. см

Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина приняла определенное значение, называется условным законом распределения.

 Условный закон распределения можно задавать как функцией распределения так и плотностью распределения.

34. Характеристики положения и рассеивания системы случайных величин. См

35. Корреляционный момент и коэффициент корреляции двух случайных величин.

Корреляционным моментом двух случайных величин X и Y называют математическое ожидание произведения отклонений этих величин: m_xy = M{[X - M(X)]Ч[Y - M(Y)]}. Корреляционный момент служит для характеристики связи между величинами X и Y. Корреляционный момент двух независимых случайных величин X и Y равен нулю. Если корреляционный момент не равен нулю, то X и Y - зависимые случайные величины

Коэффициентом корреляции случайных величин X и Y называют отношение корреляционного момента к произведениюсредних квадратичных отклонений этих величин: r_xy = m_xy / (s_xs_y).       Коэффициент корреляции является безразмерной величиной, то есть не зависит от выбора единиц измерения случайных величин X и Y. Коэффициент корреляции служит для характеристики связи между величинами X и Y и как мера линейной связи. Коэффициент корреляции двух независимых случайных величин X и Y равен нулю (так как m_xy = 0).       Коэффициент корреляции двух нелинейно зависимых случайных величин X и Y может быть равен нулю. Если коэффициент корреляции не равен нулю, то X и Y - линейно зависимые случайные величины.

36. Понятие о корреляционной матрице.

Например, для трёх x₁, x₂, x₃ величин корреляционная матрица будет иметь вид:

 

В данном случае r_ij – это коэффициент корреляции между i-ой и j-ой характеристиками и очевидно, что он равен  r_ji  (r_ij=r_ji), а также r_ii=1 для всех допустимых значений i. Поэтому для упрощения корреляционную матрицу принято представлять в треугольном виде:

37. Законы распределения системы случайных величин. См

38. Числовые характеристики системы случайных величин.??

Числа, назначение которых в сжатом виде характеризовать основные особенности распределений случайных величин, называются числовыми характеристиками см тетр (МО и дисперсия)

39. Теоремы о числовых характеристиках. ???

40. Сложение случайных величин??. Композиция законов распределения. http://it.fitib.altstu.ru/neud/om/index.php?doc=teor&module=2

41. Понятие о предельных теоремах теории вероятностей.??

42. Закон больших чисел.

Закон больших чисел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения.

Слабый закон больших чисел

Пусть есть бесконечная последовательность (последовательное перечисление) одинаково распределённых и некоррелированных случайных величин  , определённых на одном вероятностном пространстве  . То есть их ковариация  . Пусть  . Обозначим   выборочное среднее первых  членов:

.

Тогда  .

[Усиленный закон больших чисел

Пусть есть бесконечная последовательность независимых одинаково распределённых случайных величин  , определённых на одном вероятностном пространстве  . Пусть  . Обозначим   выборочное среднее первых   членов:

.

Тогда   почти наверное.

43. Центральная предельная теорема.

Центра́льные преде́льные теоре́мы (Ц.П.Т.) — класс теорем в теории вероятностей, утверждающих, что сумма большого количества независимых случайных величин имеет распределение близкое кнормальному. Так как многие случайные величины в приложениях являются суммами нескольких случайных факторов, центральные предельные теоремы обосновывают популярность нормального распределения. Классическая формулировка Ц.П.Т.  Править

Пусть   суть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию. Обозначим последние μ иσ2 соответственно. Пусть  . Тогда

 по распределению при  .

Обозначив символом   выборочное среднее первых n величин, то есть  , мы можем переписать результат центральной предельной теоремы в следующем виде:

 по распределению при  .

44. Задачи и объекты математической статистики.

Первая задача математической статистики - указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.

Вторая задача математической статистики - разработать методы анализа статистических данных в зависимости от целей исследования.

Современная математическая статистика разрабатывает способы определения числа необходимых испытаний до начала исследования, в ходе исследования и решает многие другие задачи. Современную математическую статистику определяют как науку о принятии решений в условиях неопределенности

Итак, задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.

основной объект, изучаемый математической статистикой, - случайная величина - является основным объектом изучения и для эмпирической социологии. 

45. Эмпирические распределения.????

Выборочная (эмпири́ческая) фу́нкция распределе́ния в математической статистике - это приближение теоретическойфункции распределения, построенное с помощью выборки из него.

46. Точечные оценки неизвестных параметров генеральной совокупности.

Точечные оценки представляют собой определенные значения параметров генеральной совокупности, полученные по выборочным данным. Эти значения должны быть максимально близки к значениям соответствующих параметров генеральной совокупности, которые являются истинными значениями оцениваемых параметров. Начнем с точечных оценок и рассмотрим оценку произвольного параметра (среднего, дисперсии или какого-то другого) генеральной совокупности, который обозначим . Оценивая параметр  по выборке, находим такую величину _В, которую принимаем за точечную оценку параметра . Естественно, при этом стремимся, чтобы оценка была в определенном смысле наилучшей, поэтому к ней предъявляется ряд требований:

1. Состоятельность. Точечная оценка _В называется состоятельной, если при неограниченном увеличении объема выборки ( ) она стремится к истинному значению параметра .

В математической статистике показывается, что состоятельной оценкой генерального среднего значения  , является выборочное среднее арифметическое  , а состоятельной оценкой генеральной дисперсии   — выборочная дисперсия  . Методы вычисления этих выборочных характеристик были рассмотрены в гл. 3.

2. Несмещенность. Оценка _В называется несмещенной, если она не содержит систематической ошибки, т. е. среднее значение оценки, определенное по многократно повторенной выборке объема n из одной и той же генеральной совокупности, стремится к истинному значению соответствующего генерального параметра .

Выборочное среднее арифметическое   является несмещенной оценкой генерального среднего  .

Несмещенной оценкой генеральной дисперсии   является исправленная выборочная дисперсия, вычисляемая по формуле:

 для несгруппированных данных,

 для сгруппированных данных,

3. Эффективность. Несмещенная оценка является эффективной, если она имеет наименьшую дисперсию по сравнению с другими несмещенными оценками того же параметра генеральной совокупности.

Это надо понимать так: полученные по выборке оценки   и S² — случайные величины, так как случайны сами выборочные значения. Поэтому можно говорить о математическом ожидании и дисперсии оценок   и S². Эффективность этих оценок означает, что их дисперсии D( ) и D(S²) меньше дисперсий любых других несмещенных оценок среднего значения и дисперсии генеральной совокупности.

Итак, наилучшими в указанном смысле оценками генерального среднего значения и генеральной дисперсии являются выборочные характеристики  ,  .

47. Обработка результатов наблюдений.?? Группировка опытных данных.

По результатам измерений чаще всего рассчитывают среднее арифметическое значение и статистическое среднее квадратическое отклонение (СКО) величины. Первое является оценкой математического ожидания величины, а статистическое СКО – оценкой теоретического СКО.

48. Нахождение точечных оценок генеральных параметров по интервальному статистическому ряду.

49. Понятие о доверительном интервале и доверительной вероятности для неизвестного генерального параметра.

51. Нахождение доверительных интервалов для параметров нормального распределения.

52. Проверка гипотезы о нормальном распределении обследуемого признака с помощью критерия Пирсона.

53. Построение гипотетической теоретической нормальной кривой.

54. Постановка задачи сглаживания экспериментальных зависимостей.

55. Метод наименьших квадратов.

56. Принцип максимального правдоподобия.

57. Корреляционный и регрессионный анализ, их задачи.

58. Анализ линейной корреляции по данным случайной выборки

59. Нахождение выборочного коэффициента корреляции и доверительного интервала дл него.

60. Нахождение функции регрессии в случае линейной модели.

ВОПРОСЫ ДЛЯ САМОСТОЯТЕЛЬНОГО ИЗУЧЕНИЯ

ПО ДИСЦИПЛИНЕ

«ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»

Тема 2. Основы теории вероятностей.

1. Производящая функция случайной величины.

2. Полиномиальный закон распределения случайной величины.

3. Гипергеометрический закон распределения случайной величины.

4. Логарифмически-нормальный закон распределения случайной величины.

5. Геометрический закон распределения случайной величины.

6. Отрицательный биномиальный закон распределения случайной величины.

7. Некоторые распределения, связанные с нормальным распределением.

8. Многомерный нормальный закон.

Тема 3. Статистическое оценивание.

9. Несмещённость, состоятельность, эффективность точечных оценок.

10. Распределение Стьюдента (t – распределение).

11. Распределение Фишера - Снедекора (F- распределение).

12. Распределение выборочного коэффициента корреляции.

Тема 4. Проверка статистических гипотез.

13. Статистическая гипотеза. Нулевая и конкурирующая гипотезы. Простые и сложные гипотезы.

14. Ошибки первого и второго рода. Уровень значимости. Мощность критерия.

15. Проверка гипотез о равенстве параметров генеральной совокупности (доли, средней и дисперсии) заданными значениями (стандартами).

16. Проверка гипотезы о равенстве вероятностей (генеральных долей).

17. Проверка гипотезы о равенстве дисперсий двух и нескольких нормально распределённых генеральных совокупностей.

18. Проверка гипотезы о равенстве генеральных средних двух нормально распределённых генеральных совокупностей.

19. Критерий согласия. Выбор вида и оценка параметров эмпирического закона распределения (общие понятия).

Тема 5. Дисперсионный анализ.

20. Основные понятия дисперсионного анализа. Модели: случайная, детерминированная, смешанная.

21. Формула разложения дисперсии. Однофакторный и многофакторный дисперсионный анализ. Понятие о трёхфакторном анализе.

Составила старший преподаватель Н.Р. Полуян