
- •9.Общее решение совместной неоднородной системы линейных алгебраических уравнений.
- •10. Определение линейного (векторного) пространства, действительного и комплексного. Простейшие свойства. Примеры линейных пространств.
- •11. Линейно зависимые и линейно независимые системы векторов. Критерий линейной зависимости. Достаточное условие линейной зависимости.
- •14. Матрица перехода от одного базиса линейного пространства к другому. Преобразование координат вектора при изменении базиса
- •15. Определение линейного подпространства. Свойства линейного подпространства
- •16. Определение линейной оболочки системы векторов.
- •17. Сумма и пересечение подпространств. Прямая сумма подпространств.
- •18. Определение линейного оператора. Простейшие свойства. Примеры.
- •19. Матрица оператора в базисе. Примеры.
- •21. Матрица суммы операторов, произведения оператора на число и произведения операторов.
- •22. Обратный оператор для данного линейного оператора и его свойства. Критерий обратимости линейного оператора. Примеры обратимых и необратимых операторов.
- •23. Преобразование матрицы линейного оператора при изменении базиса. Подобные матрицы.
- •24. Характеристический многочлен матрицы. Характеристический многочлен линейного оператора, его инвариантность.
- •32. Определение евклидова пр-ва. Норма вектора. Неравенство Коши-Буняковского и нер-во треугольника. Угол между двумя векторами.
- •33. Ортонормированные базисы (онб) евклидова пр-ва. Теорема о существовании онб, процесс ортогонализации Шмидта.
- •34. Ортогональные матр. , их св-ва. Переход от одного онб к другому в евклидовом пр-ве.
- •35. Самосопряженные операторы в евклидовом пр-ве, их св-ва.
- •36. Спектральная теорема самосопряженного оператора
- •37. Приведение квадратичной формы к главным осям в евклидовом пространстве.
35. Самосопряженные операторы в евклидовом пр-ве, их св-ва.
Определение. Оператор А евклид. пр-ва εn наз-ся самосопряженным, если ∀x, y∈εn: (Ax, y)=(x, Ay)
Св-ва самосопряженного оператора.
x, y∈εn, А∈L(εn).
[e]=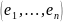 — ОНБ
— ОНБ
[e]: A↔Aе – матр. А в [e]ю
1°
Операт.
А явл. самосопр. , т. и т.т., когда ∀
ij
– 1, …, n,
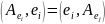
Необходимость: очевидна
Достаточность:
Пусть
∀x,
y∈εn,
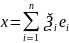 ,
,
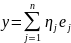
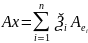 ;
;
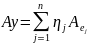
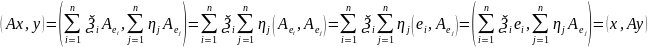
2° Оператор А явл. Самосопряж. т. т т.т., когда матр. Ае в произв. ОНБ явл. симметричной.
Док-во:
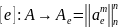
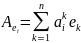 ,
,
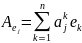
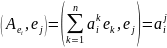
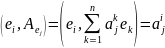
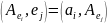 ,
т.е..
,
т.е..
 – симметричн. (т.е..
– симметричн. (т.е..
 ).
).
3° Теорема
Все корни характерист-го многочл. симметричной матрицы действ. числа (без док-ва).
4° Всякий самосопряж. оператор имеет собств. вектор.
Док-во:
Пусть
А – самосопряж. , [e]
– ОНБ; A↔
Aе
симметричная. Все собств. знач. А –
действ. корни мн-на
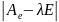 по
св-ву 3° мн-н имеет действ. корень, это
собств. знач. А, → ∃
собств.
вектор.
по
св-ву 3° мн-н имеет действ. корень, это
собств. знач. А, → ∃
собств.
вектор.
5° Собств. вектора относящ. к различным собств. знач. самосопряж. оператора ортогональны.
Док-во:
∀x, y: (Ax, y)=(x, Ay)
λ1, λ2∈ℝ, λ1≠λ2, ∃е1, е2 — ненулевые.
 ;
;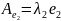 .
.
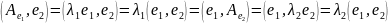
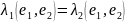 ,
т.к.. λ1≠λ2,
то
,
т.к.. λ1≠λ2,
то
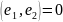 ,
то есть
,
то есть
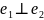 .
.
36. Спектральная теорема самосопряженного оператора
Теорема: линейный оператор А евклидова пространства En является самосопряженный тогда и только тогда, когда в En ∃ ортонормированный базис, состоящий из собственных векторов вектора A.
Док-во:
Пусть в [e] – ортонормированный базис пространства En A ⇔Ae
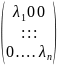
Когда
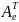 =
Ae=>A
самосопряженный
=
Ae=>A
самосопряженный
Пусть А- самосопряженный оператор En. Т.к. А самосопряженный, то ∃ — собственное значение А
и соответственно собственный вектора e1≠0, Ae1= λ1e1.Считаешь, что llexll=1, т.е. при n=1 теорема верна
Док-во:
Основ. n=1
Допустим, что теорема справедлива ∀E – евклидова пространства, dim E=n-1
Пусть dim E= n, т.е..Е=En
А самосопряженный оператор En
В En ∃e1 – собственный вектор А
Аe1= λ1e1; lle1ll=1
В En∃ базис e1, f2…fn – базис En — ОНБ
37. Приведение квадратичной формы к главным осям в евклидовом пространстве.
Определение:
говорят, что квадратичная форма q(x)
приводится к главным осям в En,
если в En
∃
ОНБ, в котором q(x)
имеет канонический вид, то есть q(x)=
λ1(
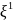 )2+…+
λn(
)2+…+
λn(
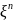 )2,
где x=
)2,
где x=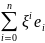
Теорема: всякая квадратичная форма приводится к главным осям.
Доказательство:
пусть q(x)-
квадратичная форма на En.
Зафиксируем в En
некоторый
ОНБ [e]:
q(x)⇿
.
То есть
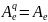 -
симметрично.
-
симметрично.
Ae – собственный линейный оператор A.
[e]: q(x) ⇿ ⇿ A (так как = , то A – самосопряженный)
Согласно
спектральной теории самосопряженного
оператора в En
∃
ОНБ [ẽ]=(ẽ1,…,ẽn)
из собственных векторов оператора A,
то есть A⇿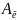 =
=
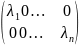 Из леммы следует, что [ẽ]:
q(x)⇿
Из леммы следует, что [ẽ]:
q(x)⇿
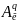 =
=
=
=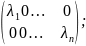 x=
x=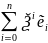 ,
то q(x)=
λ1(
,
то q(x)=
λ1(
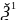 )2+…+
λn(
)2+…+
λn(
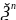 )2
.
)2
.
