Билет 1. Понятие ранга матрицы. Теорема о базисном миноре.
Определение. Минором порядка k матрицы A называется определитель матрицы k-го порядка, элементы которой стоят на пересечении выбранных k – строк и k – столбцов, т.е..
Определение. Минор порядка r матрицы A называется базисным, если он отличен от нуля, а все миноры более высокого порядка равны нулю (если они существуют)..
Определение. Рангом матрицы А называется порядок её базисного минора, т.е.. ранг матрицы A равен r, если в матрице существует ненулевой минор r-го порядка, а все миноры более высокого порядка равны нулю (если они существуют). Обозначается Rg A.
Определение. Минор, определяющий ранг матрицы, называется Базисным минором. Строки и столбцы, формирующие базисный минор, называются базисными строками и столбцами.
Теорема о базисном миноре. Столбцы матрицы А, входящие в базисный минор, образуют линейно независимую систему. Любой столбец матрицы А линейно выражается через базисные столбцы.
Доказательство. Amxn = || aij ||mxn Пусть k – порядок базисного минора. Без ограничения общности считаем, что базисный минор расположен в левом верхнем углу.
Если базисные столбцы линейно зависимы, то столбцы базисного минора так же линейно зависимы => хотя бы один из столбцов линейно выражается через остальные, т.е.. является их линейной комбинацией => Δ = 0, что противоречит условию => базисные столбцы линейно независимы.
Зафиксируем произвольный столбец матрицы А, например
.
Покажем, что
линейно
выражается через базисные столбы.
Построим определитель
(1≤ l ≤n) (1≤ i ≤m)
Если
i
< k
или l
< k,
то
Рассмотрим
случай i
> k,
l
> k
Тогда
как минор k+1–
го порядка в матрице А. Обозначим А1,
…, Аk,
Ak+1
алгебраические
дополнения к последней строке
Эти
величины не зависят от элементов i-ой
строки. Кроме того Ak+1
=
Δ
≠ 0.
Разложим минор по последней строке.
ai1
A1+…+
aik
Ak
+ ail
Δ
= 0
l
= 1, …, n
ч.т.д.
Следствие 1. Пусть Аmxn Если Rg A < n, то столбцы матрицы линейно зависимы.
Доказательство. Пусть Rg A = k < n, значит в матрице существует базисный минор порядка k. Не ограничиваясь общности будем считать, что ↓a1, …, ↓ak базисные. Т.к.. k < n, то ∃ ↓ak+1. По теореме о базисном миноре столбец ↓ak+1 выражается через базисные, т.е.. ↓a1, …, ↓ak, ↓ak+1 – линейно зависимы => матрица содержит линейно зависимую подсистему => матрица линейно зависима.
Следствие 2. Пусть А – квадратная матрица. det A = 0 столбцы матрицы линейно зависимы.
Доказательство. Если столбцы линейно зависимы, то det A = 0. Пусть det A = 0, тогда Rg A < n, т.е.. число столбцов больше ранга => (из следствия 1) столбцы матрицы линейно зависимы.
Билет 2. Понятие ранга матрицы. Теорема о ранге матрицы.
Определение. Минором порядка k матрицы A называется определитель матрицы k-го порядка, элементы которой стоят на пересечении выбранных k – строк и k – столбцов, т.е..
Определение. Минор порядка r матрицы A называется базисным, если он отличен от нуля, а все миноры более высокого порядка равны нулю (если они существуют)..
Определение. Рангом матрицы А называется порядок её базисного минора, т.е.. ранг матрицы A равен r, если в матрице существует ненулевой минор r-го порядка, а все миноры более высокого порядка равны нулю (если они существуют). Обозначается Rg A.
Определение. Минор, определяющий ранг матрицы, называется Базисным минором. Строки и столбцы, формирующие базисный минор, называются базисными строками и столбцами.
Теорема о ранге матрицы. Ранг матрицы равен максимальному числу линейно независимых столбцов этой матрицы.
Доказательство. Пусть Amxn = || aij ||mxn и Rg A = k. Если А ≠ 0, то утверждение верно. Если Rg A = k =n, то утверждение верно. Если 0 < Rg A = k < n, то т.к.. Rgрядок базисного минора, то значит А содержит k базисных столбцов (они линейно независимы). Возьмем произвольные r (r > k) столбцов матрицы А. Составим матрицу В из этих столбцов. Rg B ≤ Rg A = k. По следствию 1 в этом случае столбцы матрицы B линейно зависимы. ч.т.д.
Следствие 3. Для любой матрицы А максимальное число линейно независимых столбцов равняется максимальному числу линейно независимых строк этой же матрицы.
Билет 3. Элементарные преобразования матриц. Инвариантность ранга матрицы при помощи элементарных преобразованиях. Вычисление ранга матрицы.
Определение. Элементарные преобразования:
Перестановка строк; умножение строки на число, отличное от нуля; прибавление к одной строке другой, умноженное на число; аналогичные преобразования для столбцов матрицы.
Замечание. элементарные преобразования обратимы А~В
Теорема. Если А~В, то Rg A=Rg B
Доказательство.
Пусть
Rg
A
= r
А
=>
∃Mr≠0,
а все Mr+1=0.
Рассмотрим произвольный минор
в
матрице
не содержит левую строку, тогда =Mr+1=0
не содержит второй строки =Mr+1 + λM’r+1 = 0, Mr+1 –минор из А => Mr+1 = 0. M’r+1 – минор матрицы А
содержит 1 и 2 строку. = M r+1 + λM’r+1 = 0. M’r+1 – совпадают 1 и 2 строки. M r+1= M’r+1 = 0
В все миноры = 0 => Rg ≤ r = Rg A. Т.к.. элементарные преобразования обратимы, то ~ A => Rg A ≤ Rg ≤ Rg A => Rg A = Rg ч.т.д.
Определение. Говорят, что матрица А имеет ступенчатый вид, если: 1) Ниже нулевой строки располагаются нулевые строки. 2) если ai 1 = … = ai k-1 = 0, ai k ≠ 0, то ai k = 1 ∀ s > i и ∀ t ≤ k: as t = 0
ступенчатая
матрица. Замечание.
Ранг
ступенчатой матрицы равен числу
ненулевых строк.
Билет 4. Критерий совместимости систем ЛАУ (теорема Кронкеля – Капелли).
(1) Система ЛАУ из m уравнений с n неизвестными; = (A|b↓) = (↓a1 … ↓an | b↓) – расширенная матричная система (1); Ax↓ = b↓ ↓a1x1+…+↓anxn = b↓ (1’)
Определение. Система ЛАУ называется совместной, если она имеет хотя бы одно решение.
Теорема Кронкеля – Капелли. Система ЛАУ совместна в том и только в том случае, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е.. Rg A = Rg
Доказательство. Необходимость. Пусть система совместна => существуют решения (α1… αn)T. Подставим их в (1’): ↓a1 α1+…+↓an αn = b↓; Rg = Rg(↓a1 … ↓an | b↓) = Rg(↓a1 … ↓an | b↓ — ↓a1 α1-…-↓an αn) = Rg(↓a1 … ↓an | 0↓) = Rg(A|0↓) = Rg A
Достаточность. Пусть Rg A = Rg => базисный минор матрицы А является базисным минором матрицы => столбец b↓ линейно выражается через базисные столбцы матрицы А, т.е.. ∃ (α1… αn) такие, что b↓ = ↓a1 α 1+…+↓an α n => (α 1… α n)T – решение системы (1). ч.т.д.
Билет 5. Метод Гаусса решения систем ЛАУ.
Пусть исходная система выглядит следующим образом
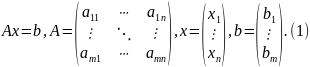
Матрица A называется основной матрицей системы, b — столбцом свободных членов. Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):
При этом будем считать, что базисный минор основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных xj1, …, xjr. Тогда переменные xj1, …, xjr называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число βi≠0, где i>r, то рассматриваемая система несовместна.
Пусть
βi=0
для любых i>r.
Перенесём свободные переменные за
знаки равенств и поделим каждое из
уравнений системы на свой коэффициент
при самом левом x
(
,
где i
— номер строки):
,
где i=1,
…r,
k=i+1,
…, n.
Если свободным переменным системы (2)
придавать все возможные значения и
решать новую систему относительно
главных неизвестных снизу вверх (то
есть от нижнего уравнения к верхнему),
то мы получим все решения этой СЛАУ.
Так как эта система получена путём
элементарных преобразований над
исходной системой (1), то по теореме об
эквивалентности при элементарных
преобразованиях системы (1) и (2)
эквивалентны, то есть множества их
решений совпадают.
Следствие: Если в совместной системе все переменные главные, то такая система является определённой, а если количество переменных в системе превосходит число уравнений, то такая система является либо неопределённой, либо несовместной.
Билет 6. Однородные системы ЛАУ. Свойства решений. Критерий наличия ненулевых решений.
Однородной системой линейных уравнений называется система вида:
Нулевое
решение
системы (1) называется тривиальным
решением.
Теорема Критерий существования ненулевых решений однородной системы ЛАУ. Однородные системы ЛАУ имеют ненулевое решение тогда и только тогда, когда ранг матрицы системы меньше числа неизвестных.
Доказательство.
Система
(1) имеет ненулевое решение в том и только
в том случае, когда столбцы матрицы А
линейно зависимы, т.е.. ∃
числа
,
не все равные нулю и такие что:
С другой стороны столбцы матрицы А
линейно зависимы тогда и только тогда,
когда Rg
a
< n
– числа столбцов в А. ч.т.д.
Теорема. Если ↓x(1) и ↓x(2)решение системы (1), то любых чисел α и β линейная комбинация α↓x(1) + β↓x(2) – решение системы (2).
Доказательство. По условию А↓x(1) = 0↓ А↓x(2) = 0↓ подставим в (1) линейную комбинацию α↓x(1) + β↓x(2): А(α↓x(1) + β↓x(2)) =А(α ↓x(1)) + А(β↓x(2)) = αА↓x(1) + βА↓x(2) = 0↓ + 0↓ = 0↓
Замечание. Теорема справедлива, если ↓x(1), ↓x(2), …, ↓x(k) – решение системы (2), а α1, α2, …, αk – числа, т.е.. α1↓x(1) +…+αk↓x(2) – решение системы (2).
Билет 7. ФСР однородной системы уравнений. Теорема о существовании ФСР.
(1)
Определение. Пусть n- число неизвестных, r = Rg A однородной системы ЛАУ. Фундаментальным решением системы называется любая линейно независимая система из n-r решений.
Если
Rg
A
= n,
то система имеет только нулевое решение.
Пусть r
= Rg
A
< n.
Тогда в А существует базисный минор
порядка r.
Не ограничивая общности считаем базисным
минором
.Строки
а1,
…, аr
— базисные.
По
теореме о базисном миноре строки ar+1,
…, an
линейно
выражаются через базисные, т.е.. все
уравнения системы являются линейными
комбинациями первых r
уравнений.
(2) Система (2) эквивалентна (1)
Назовем неизвестные x1,
…, xr
–
главными неизвестными, а xr+1,
…, xn
– свободные неизвестные.
(4) Система (4) эквивалентна системе (2)
Т.к..
,
поэтому
при заданных значениях свободных
неизвестных главная неизвестная
определяется однозначно. (По теореме
Крамера.)
Теорема 7. Если r = Rg A < n, то система (1) однородной системы ЛАУ имеет n-r линейно независимых решений.
Доказательство.
– свободные неизвестные.
– линейно независимы. Rg(
)
= n-r
=
8.Линейная зависимость любых (n-r+1) решений однородной системы. Общее решение однородной системы ЛАУ.
Теорема1: если r = RgA < n, то любая система из (n-r+1) решений однородной системы линейно зависима.
Доказательство: рассмотрим произвольные (n-r+1) решения однородной системы ЛАУ:
=
……
=
,
=
Создадим
матрицу B:
,
RgB
≤ n-r
< n-r+1
=>
столбцы
B
линейно зависимы
=
> существуют
такие
,
…,
,
(не все равные нулю), что будет выполнятся:
+
… +
+
=
;
=
+ … +
=
;
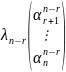- решение однородной системы ЛАУ(по критерию существования ненулевых решений)
Итак,
существуют такие
,
…,
,
(не все равные нулю), что
+ … +
=
Теорема
2: если
r=RgA
< n
и
,
…,
– ФСР однородной системы ЛАУ, то общее
решение системы имеет вид:
=
+
… +
,
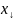где
,
…,
-
произвольные числа
Доказательство:
1) Для произвольных , …, – линейная комбинация: = , …, — решение однородной системы ЛАУ (критерий существования ненулевых решений)
2)Обратное.
Пусть
-
произвольное решение системы однородных
ЛАУ. Рассмотрим систему решений
,
…,
.
Она содержит (n-r+1)
решений = > является линейно зависимой.
Т.е.. существуют такие
,
…,
,
(не все равные нулю), что
+… +
+
=
.
Если = 0, то + … + = , причем ∣ ∣+ … +∣ ∣ ≠ 0, чего быть не может = >
≠ 0
и
=
(
+
… + (
.
Обозначим
= (
),
i
= 1… n-r,
таким образом
= + … + .
9.Общее решение совместной неоднородной системы линейных алгебраических уравнений.
(
)
A
=
;
(
)
A
=
;
Система ( ) называется приведённой однородной системой ЛАУ для неоднородной системы ( ) . n – число неизвестных, r ≤ n.
Теорема1: общее решение совместной неоднородной системы ЛАУ (1) представляется как сумма некоторого частного решения этой системы и общего решения приведённой системы.
=
+
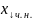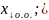– некоторое фиксированное решение
системы (1);
– общее решение (1);
– общее решение (
))
Доказательство: т.к. (1) совместна, то существует хотя бы одно решение. Фиксируем , т.е..
A =
1)
Пусть
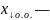произвольное
решение (
),
т.е.. A
=
.
Покажем, что (
+
)
– решение (1). Действительно,
= A
+ A
=
+
= > (
+
)
– единственное решение.
2)
Пусть
произвольное
решение (
),
т.е.. A
=
.
Рассмотрим
=
.
Подставим в (
):
A
=
= A
— A
=
—
=
;
– решение (
).
=
+
=
+
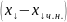Теорема2:
если
RgA
= Rg
= r,
причем r
< n
и
,
…,
– ФСР (1), а
— частное решение (1), то
=
+
+…
+
,
где
,
…,
–
произвольные числа.
(без докозательства)
Выводы:
1) RgA ≠ Rg — система неоднородных ЛАУ несовместна
2) RgA = Rg — система неоднородных ЛАУ совместна
а) RgA = r = n – система имеет единственное решение
б) RgA = r < n — система имеет бесконечно много решений.
10. Определение линейного (векторного) пространства, действительного и комплексного. Простейшие свойства. Примеры линейных пространств.
Опр. Непустое множество V элементов произвольной природы называется действительным линейным пространством, если:
а) Любым двум элементам x и y ∈ V поставлен в соответствие элемент z ∈ V, который называется суммой элементов x и y и обозначается z = x+y.
б) Любому элементу x ∈ V и любому числу λ ∈ ℝ (ε) поставлен в соответствие элемент λ х ∈ V, который называется произведением элемента x на число λ.
При этом выполняются следующие аксиомы:
1о. ∀x,y ∈ V : x+y=y+x
2о. ∀x,y,z ∈ V: (x+y)+z=x+(y+z)
3о. ∃ элемент θ ∈ V: ∀x ∈ V: x+θ=x
4о. ∀x ∈ V ∃ x’ ∈ V: x+x’= θ (x’= -x)
5о. (α+ β)x= αx+ βx
6о. (α β)x= α (βx)
7о. 1*x=x
Простейшие свойства линейного пространства V:
1.Единственность нулевого элемента
Док-во. Допустим ∃ θ1 и θ2 ∈ V- нулевые элементы, тогда
θ1=θ1+θ2=θ2+θ1=θ2
2.Единственность противоположного элемента
Док-во. Пусть x ∈ V и ∃ x’ и x’’ ∈ V : x+x’= θ и х+x’’= θ
x’= x’+θ= x’+(x+x’’)=(x’+x)+x’’=(x+x’)+x’’=θ+x’’=x’’+θ=x’’
3. ∀x ∈ V : 0*x= θ
Док-во. 0*x=0*x+θ=0*x+(x+x’)=(0*x+x)+x’=(0*x+1*x)+x’=(0+1)*x+x’=1*x+x’=x+x’=θ
4. ∀x ∈ V : (-x)=(-1)*x
Док-во. x+(-1)*x=1*x+(-1)*x=(1+(-1))*x=0*x=θ, т.к. ∃!θ, что (-x)=(-1)*x
5. ∀ α ∈ ℝ : α*θ=θ
Док-во. α*θ=α*(0*θ)=(α*0)*θ=0*θ=θ
6. ∀ α ∈ ℝ : α*(-x)=(-α)*x=-(α*x)
Док-во. α*(-x)=α*((-1)*x)= (α*(-1))*x=(-α)*x=-(α*x)
7. α*x= θ ⟹ либо α=0, либо x=θ;
Док-во. Если α=0, то получаем 3о
Если x= θ , то получаем 5о