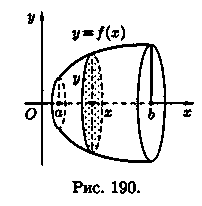12) Интегрирование по частям и заменой переменных.

Пусть функция определена и дифференцируема на некотором множестве и пусть – множество всех значений этой функции. Пусть далее для функции существует множество первообразная функция . . Тогда всюду на множестве для функции существует первообразная функция, равная , т.е. . Для доказательства достаточно воспользоваться правилом дифференцирования сложной функции: и учесть, что по определению первообразной . Предположим теперь, что нам требуется вычислить интеграл . В качестве новой переменной выберем что причем функция g(t) легко интегрируется, т.е.: просто вычисляется.

Интегрирование путем замены переменной

Замена:

Интегрирование по частям

Пусть каждая из функций и дифференцируема на множестве и, кроме того, на этом множестве существует первообразная для функции . Тогда на множестве существует первообразная и для функции , причем справедлива формула:

Замечание: Определение дифференциала и свойство инвариантности его формы позволяет записать формулу в виде

Для доказательства утверждения запишем формулу для производной произведения 2-х функций и : . Умножим равенство на и возьмем интеграл от обеих частей равенства. Так как по условию для всех из множества существует и , то для всех множества существует интеграл , причем справедлива формула: . Эта формула сводит вопрос о вычислении интеграла к вычислению . .

1) Определённый интеграл. Интегральная сумма. Верхние и нижние интегральные суммы. Их свойства. Геометрический смысл определённого интеграла.

Пусть на некотором промежутке задана функция .

Произведём разбиение отрезка точками . Внутри каждого отрезка возьмём произвольную точку .

- интегральная сумма.

Устремим . Максисум - мелкость разбиения (характеристика разбиения).

Фигура под кривой называется криволинейной трапецией.

- определение определенного интеграла (если предел существует).

Интегральные суммы и их свойства:

Нижняя интегральная сумма: , где

Верхняя интегральная сумма: , где

1) , при данном конкретном разбиении.

2) если разбиение получается из разбиения T добавлением одной точки разбиения, то нижняя интегральная сумма может только увеличиться, а верхняя только уменьшиться, т.е.

Следствие: при добавлении к любому разбиению T любого дополнительного числа точек разбиения нижняя интегральная сумма может только увеличиться, а верхняя - только увеличиться.

3) Для любых 2-х разбиений T' и T'', нижняя интегральная сумма любого разбиения не превосходит интегральную сумму другого разбиения .

Доказательство: по предыдущему свойству рассмотрим разбиение T, полученное из всех точек разбиения T' и T''. Тогда . Аналогично . И т.к. , то , что и требовалось доказать.

4) Все нижние интегральные суммы ограничены сверху, а все верхние интегральные суммы ограничены снизу. Как известно, множество чисел, ограниченных сверху имеют точную верхнюю грань аналогично и для ограниченных снизу - нижняя грань .

- верхняя грань для s.

- верхняя грань для S.

Геометрический смысл определенного интеграла - это площадь фигуры, ограниченной прямыми , осью и графиком функции .

5) Основные свойства определённого интеграла.

1) ;

2) ; (следует из определения интеграла как предела интегральных сумм).

3) ;

4) ;

5) ;

6) ;

7) ;

6) Теорема о среднем для определённого интеграла.

Если -неотрицательная функция на промежутке и ограничена на нём, то Проинтегрируем:

; разделим все на

.

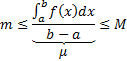
Следствие: если - непрерывна на отрезке , то она принимает все значения от до , в том числе и .

19) Критерий интегрируемости ограниченной на отрезке функции.

Критерии интегрируемости.

Необходимое условие: функция f должна быть ограниченной на отрезке [a,b].

 

Критерий Коши:

Для существования неопределенного интеграла необходимо и достаточно, чтобы 

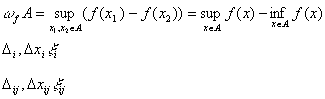
Достаточный признак:

Для интегрирования f достаточно. 

.

Доказательство:

В отрезке 

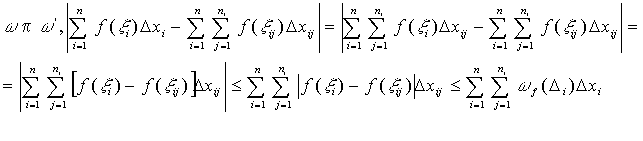Пусть  , тогда 

 

 f интегрируемая функция, ч.т.д.

Следствие №1

Если функция f ограничена на [a, b] и имеем на нем конечное число точек разрыва, то функция fинтегрируема на [a, b].

Доказательство:

Пусть f имеет на [a, b] k-точек разрыва

Рассмотрим у каждой точки разрыва с радиусом   и вычтем из отрезка

                                               +         

 выберем  , такое, что  ;

 ;  {берётся по отрезкам, которые не пересекаются с окрестностью точек разрыва}+ {все остальные}

<    ч.т.д.

4) Теорема об интегрируемости непрерывной на отрезке функции.

Следствие №2

Если функция f непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.

Доказательство:

f - непрерывна на [a, b]  она равномерно непрерывна 

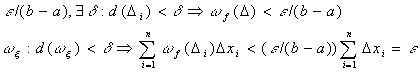ч.т.д.

4) Теорема об интегрируемости монотонной на отрезке функции.

Следствие №3

Если f(x) ограничена и монотонна на [a, b], то она интегрируема на этом отрезке.

Доказательство:

  ; 

 в силу монотонности функции все разности под знаком модуля в получившейся сумме имеют один знак

 {т.к.   и  }=  ч.т.д.

7) Интеграл с переменным верхним пределом. Производная интеграла с переменным верхним пределом.

Рассмотрим функцию f (x), интегрируемую по Риману на отрезке [a, b]. Раз она интегрируема на [a, b], то она также интегрируема на [a, x] ∀x ∈ [a, b]. Тогда при каждом x ∈ [a, b] имеет смысл выражение , и при каждом x оно равно некоторому числу.

Таким образом, каждому x ∈ [a, b] поставлено в соответствие некоторое число ,

т.е. на [a, b] задана функция:

(3.1)

Определение. Функция F (x), заданная в (3.1), а также само выражение называется

интегралом с переменным верхним пределом. Она определена на всем отрезке [a, b]

интегрируемости функции f (x).

Теорема

Усл. f (t) непрерывна на [a, b], а функция F (x) задана формулой (3.1).

Утв. Функция F(x) дифференцируема на [a, b], причем F (x) = f (x).

(В точке a она дифференцируема справа, а в точке b – слева.)

Доказательство. Поскольку для функции одной переменной F (x) дифференцируемость равносильна существованию производной во всех точках (в точке a справа, а в точке b – слева), то мы найдем производную F (x). Рассмотрим разность

Таким образом,

,

при этом точка ξ лежит на отрезке [x, x + ∆x] (или [x + ∆x, x] если ∆x < 0).

Теперь вспомним, что производная функции F(x) в заданной точке x ∈ [a, b] равна пределу разностного отношения: . Из равенства имеем:

,

Устремляя теперь ∆x → 0, в левой части данного равенства получим F’(x), a в правой

Вспомним определение непрерывности функции f (t) в точке x:

Пусть x1 в этом определении равен ξ. Поскольку ξ ∈ [x + ∆x, x] (ξ ∈ [x, x + ∆x]), а

∆x → 0, то |x − ξ| → 0, и по определению непрерывности, f (ξ) → f (x). Отсюда имеем:

F’(x) = f (x).

Следствие

Усл. f (x) непрерывна на [a, b].

Утв. Любая первообразная функции f (x) имеет вид

где C ∈ R – некоторая константа.

Доказательство. По теореме 3.1 функция является первообразной для f(x). Предположим, что G(x) – другая первообразная f (x). Тогда G’(x) = f(x) и для функции F(x) − G(x) имеем: (F (x) + G(x))’ = F’(x)−G’(x) = f (x)−f(x) ≡ 0. Значит, производная функции F (x)−G(x)

равна нулю, следовательно, эта функция есть постоянная: F(x) − G(x) = const.

Теорема 9.9.1. Пусть функция интегрируема на отрезке . Тогда интеграл с переменным верхним пределом интегрирования непрерывен на отрезке .

Доказательство. Так как функция интегрируема на отрезке , то она ограничена на нем, т. е. существует число такое, что для всех . Пусть -- любая точка из и -- произвольное. Используя свойства интеграла, получим

Следовательно,

Итак, для заданного число таково, что для всех со свойством

т. е. функция непрерывна в точке .

Теорема 9.9.2. Если функция интегрируема на отрезке и непрерывна в точке , то функция дифференцируема в точке и .

Доказательство. Ввиду непрерывности функции в точке для любого существует такое, что для всех выполняется . Тогда для любого выполняется

Итак,

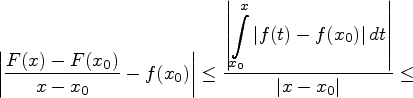
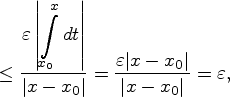
что, по определению, означает дифференцируемость функции в точке .

8) Формула Ньютона – Лейбница.

Теорема

Усл. f(t) непрерывна на [a, b], а F(x) ее любая первообразная.

Утв.

Доказательство. Рассмотрим некоторую первообразную F (x) функции f (x). По Следствию 3.1 она имеет вид . Отсюда

=> c=F(a), и

.

Перенесем F(a) в последнем равенстве в левую часть, переобозначим переменную интегрирования снова через x и получим формулу Ньютона – Лейбница:

Замечание 3.1. Доказанное равенство

называется формулой Ньютона – Лейбница.

9. Методы вычисления определенного интеграла

Теорема 9.10.1. Для непрерывно дифференцируемых на отрезке функций имеет место формула интегрирования по частям

Доказательство. Функция непрерывно дифференцируема на отрезке . По теореме 9.9.5 имеем

Но по правилу дифференцирования произведения

Следовательно, слагаемые непрерывны и по аддитивному свойству определенного интеграла получаем

Отсюда следует требуемое равенство.

Последнюю формулу удобно записывать в виде

Пример 9.10.1. Вычислим интеграл .

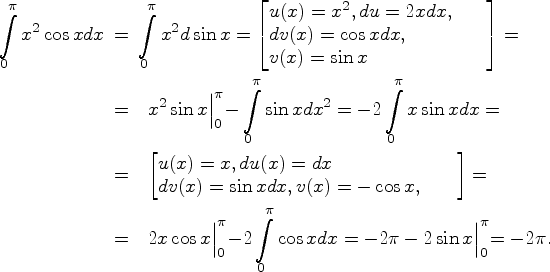
Теорема 9.10.2. Если функция непрерывно дифференцируема на отрезке , при лю- бом значения функции лежат на отрезке , и функция непрерывна на отрезке , тогда имеет место формула замены переменной :

Доказательство (см. рис. 9.10.1). По теореме 8.2.1 о замене переменной в неопределенном интеграле функции и имеют непрерывно дифференцируемые первообразные и , связанные между собой так: для всех . По теореме Ньютона - Лейбница имеем

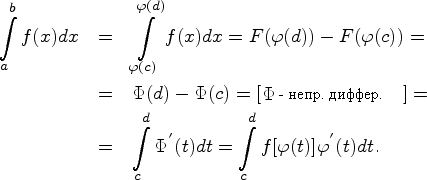
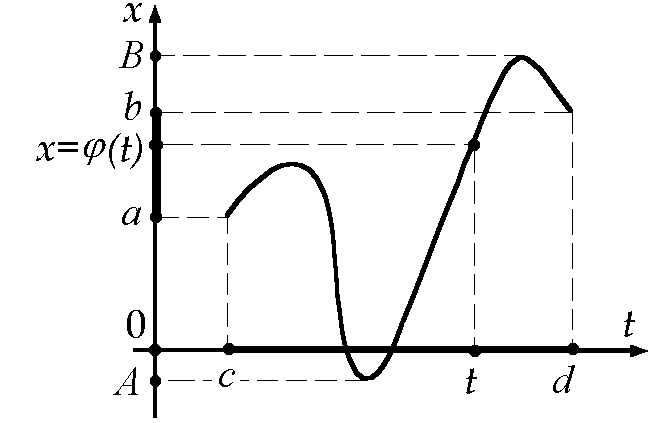
Рис. 9.10.1

Пример 9.10.2

10) Геометрические приложения определённого интеграла: площади плоских фигур, длина кривых. Вычисление объёма тел, в том числе тел вращения.

Вычисление площадей плоских фигур

Прямоугольные координаты

Площадь криволинейной трапеции, расположенной «выше» оси абсцисс (ƒ(х) ≥ 0), равна соответствующему определенному и нтегралу:

Формула (41.1) получена путем применения метода сумм. Пусть криволинейная трапеция ограничена линиями у = ƒ(х) ≥ 0, х = а, х = b, у = 0 (см.  рис. 174).

Для нахождения площади S этой трапеции проделаем следующие операции:

1. Возьмем произвольное х  [а; b] и будем считать, что S = S(x).

2. Дадим аргументу х приращение Δх = dx (х + Δх є [а; b]). Функция S = S(x) получит приращение ΔS, представляющее собой площадь «элементарной криволинейной трапеции» (на рисунке она выделена).

Дифференциал площади dS есть главная часть приращения ΔS при Δх → 0, и, очевидно, он равен площади прямоугольника с основанием dx и высотой у: dS = у • dx.

3. Интегрируя полученное равенство в пределах от х = а до х = b, получаем

Отметим,что если криволинейная трапеция расположена «ниже» оси Ох (ƒ(х) < 0), то ее площадь м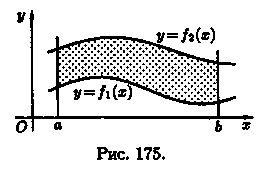 ожет быть найдена по формуле

Формулы (41.1)и (41.2) можно объединить в одну:

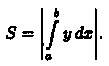
Если криволинейная трапеция ограничена прямыми у = с и у=d, осью Оу и непрерывной кривой х = φ(у) ≥ 0 (см. рис. 177), то ее площадь находится по ф ормуле

И, наконец, если криволинейная трапеция ограничена кривой, заданной параметрически

прямыми х = а и х = b и осью Ох, то площадь ее находится по формуле

где а и β определяются из равенств х(а) = а и х(β) =b.

  

Полярные координаты

Найдем площадь S криволинейного сектора, т. е. плоской фигуры, ограниченной непрерывной линией r=r(φ) и двумя лучами φ=а и φ=β (а < β), где r и φ — полярные координаты (см. рис. 180).

1. Будем считать часть искомой площади S как функцию угла φ, т. е. S = S(φ), где а ≤φ≤β (если φ = а, то S(a) = 0, если φ=β, то S(β) = S).

2. Если текущий полярный угол φ получит приращение Δφ = dφ, то приращение площади AS равно площади «элементарного криволинейного сектора» OAB.

Дифференциал dS представляет собой главную часть приращения ΔS при dφ→0 и равен площади кругового сектора О АС (на рисунке она  заштрихована) радиуса r с центральным углом dφ. Поэтому

3. Интегрируя полученное равенство в пределах от φ = а до φ = β, получим искомую площадь

 

Вычисление длины дуги плоской кривой

Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у=ƒ(х), где а≤х≤ b.

Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Покажем, что если функция у=ƒ(х) и ее производная у' = ƒ'(х) непрерывны на отрезке [а; b], то кривая АВ имеет длину, равную

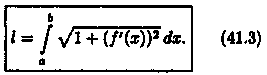
1. Точками х₀ = а, х₁..., х_n = b (х₀ < x₁ < ...< х_n) разобьем отрезок [а; b] на n частей (см. рис. 183).  Пусть этим точкам соответствуют точки М₀ = А, M₁,...,M_n =В на кривой АВ. Проведем хорды М₀M₁, M₁M₂,..., М_n-1М_n, длины которых обозначим соответственно через ΔL₁, AL₂,..., ΔL_n. Получим ломаную M₀M₁M₂ ... M_n-ιM_n, длина которой равна L_n=ΔL₁ + ΔL₂+...+ ΔL_n =

2. Длину хорды (или звена ломаной) ΔL₁ можно найти по теореме Пифагора из треугольника с катетами Δx_i и Δу_i:

По теореме Лагранжа о конечном приращении функции Δу_i=ƒ'(с_i)•Δх_i, где ci є (x_i-1;x_i). Поэтому

а длина всей ломаной M₀M₁... М_n равна

3.Длина l кривой АВ, по определению, равна

.

 Заметим, что при ΔL_i→0 также и Δx_i →0 ΔLi = и, следовательно, |Δx_i|<ΔL_i).

Функция непрерывна на отрезке [а; b], так как, по условию, непрерывна функция ƒ'(х). Следовательно, существует предел интегральной суммы (41.4), когда max Δx_i→ 0:

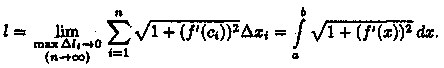
Таким образом,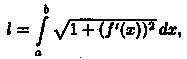 или в сокращенной записи  l =

Вычисление объема тела

Вычисление объема тела по известным площадям параллельных сечений

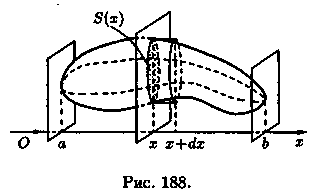
Пусть требуется найти объем V тела, причем известны площади S сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси Ох: S = S(x), а ≤ х ≤ b.

1. Через произвольную точку х є [a;b] проведем плоскость ∏, перпендикулярную оси Ох (см. рис. 188). Обозначим через S(x) площадь сечения тела этой плоскостью; S(x) считаем известной и непрерывно изменяющейся при изменении х. Через v(x) обозначим объем части тела, лежащее левее плоскости П. Будем считать, что на отрезке [а; х] величина v есть функция от х, т. е. v = v(x)  (v(a) = 0, v(b) = V).

2. Находим дифференциал dV функции v = v(x). Он представляет собой «элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими ось Ох в точках х и х+Δх, который приближенно может быть принят за цилиндр с основанием S(x) и высотой dx. Поэтому дифференциал объема dV = S(x) dx.

3. Находим искомую величину V путем интегрирования dA в пределах от а до В:

Полученная формула называется формулой объема тела по площади параллельных сечений.

 

Объем тела вращения

Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная непрерывной линией у = ƒ(х)  0, отрезком а ≤ x ≤ b и прямыми х = а и х = b (см. рис. 190). Полученная от вращения фигура называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси Ох (х  [а; b]), есть круг с радиусом у= ƒ(х). Следовательно, S(x)=πy^2.

Применяя формулу (41.6) объема тела по площади параллельных сечений, получаем

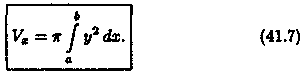
Если криволинейная трапеция ограничена графиком не прерывной функции х=φ(у) ≥ 0 и прямыми х = 0, у = с,

у = d (с < d), то объем тела, образованного вращением этой трапеции вокруг оси Оу, по аналогии с формулой (41.7), равен