
- •1.Фнп. Основные понятия. Предел и непрерывность фнп.
- •2. Частные производные фнп, их геом. Смысл. Частные производные высших порядков.
- •3.Дифф-сть фнп. Необходимые условия дифф-ти. Достаточное условие дифф-ти.
- •4. Полный дифференциал фнп и его применение в приближенных вычислениях.
- •5. Частные производные сложной функции. Полная производная функции
- •6. Производная от функции, заданной неявно.
- •7.Градиент фнп и его основные свойства.
- •8.Необх. И дост. Условия лок. Экс. Ф-ции 2 переменных.
- •15. Таблица неопределенных интегралов. Метод замены переменной в неопределенном интеграле
- •16. Метод интегрирования по частям. Некоторые типичные интегралы, берущиеся по частям.
- •17. Простейшие рациональные дроби. Метод неопределенных коэффициентов.
- •19. Интегрирование тригонометрических функций. Универсальная тригонометрическая подстановка.
- •21. Определение и геометрический смысл определенного интеграла.
- •22. Условия интегрируемости функции. Свойства определенного интеграла, его экономический смысл.
- •23. Формула Ньютона-Лейбница.
- •24. Замена переменной и интегрирование по частям в определенном интеграле.
- •25. Приложения определенного интеграла (формулы для площади плоской фигуры и для длины дуги кривой).
- •26. Несобственные интегралы первого рода, их геом. Смысл. Признаки сравнения нес. Интегралов 1-го рода.
- •27. Несобственные интегралы второго рода, их геом. Смысл. Признаки сравнения нес. Интегралов 2 рода
- •29. Повторные интегралы. Вычисление 2-ых интегралов.
- •30. Применение двойных интегралов в геометрии.
- •31.Основные понятия оДу. Т. О сущ-и и ед-ти. Задача Коши. Общий интеграл и общее решение ду. Частные решения. Геом. Смысл ду.
- •32. Ду с разделяющимися и разделен. Переменными.
- •33. Однородные ду первого порядка.
- •34. Линейные ду первого порядка. Метод Бернулли.
- •35. Лоду 2 порядка с постоянными коэффициентами.
- •36. Линейные неоднородные ду второго порядка с постоянными коэффициентами и спец. Правой частью.
- •38. Необходимой условие сходимости числового ряда. Признаки сравнения рядов с неотр. Членами.
38. Необходимой условие сходимости числового ряда. Признаки сравнения рядов с неотр. Членами.
необходимое условие сходимости числового ряда: если ряд (1) сходится, то его n -ый член стремится к нулю при n → ∞; lim n→∞ an = 0. Достаточное условие расходимости числового ряда: если n -ный член ряда не стремится к нулю при n → ∞, то ряд расходится. Для того чтобы ряд (1) с неотрицательными членами сходился, необходимо и достаточно, чтобы последовательность частичных сумм этого ряда была ограничена. признак сравнения). Пусть даны два ряда (1) и (3) с неотриц. членами и для всех n выполняется неравенство an’’bn. Тогда из сходимости ряда (3) следует сходимость ряда (1), а из расходимости ряда (1) следует расходимость ряда (3). Предельный признак сравнения: если существует конечный, отличный от нуля предел n→∞ an/bn, то ряды с положительными членами (1) и (3) сходятся и расходятся одновременно. 39. Признаки сходимости числовых рядов с неотриц. членами (признак Д’Аламбера, радикальный и интегральный признаки Коши).
признак Дaламбера:
если для членов знакоположительного
ряда ∑an
существует конечный предел n→∞
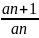 =ℓ,то
при: 1) 0 ≤ l
<1 ряд сходится; 2) l
=1 необходимы дополнительные исследования;
3) l
>1 ряд расходится.
Признак
Коши(радикальный): если для членов
знакоположительного ряда ∑an
существует конечный предел n→∞
=ℓ,то
при: 1) 0 ≤ l
<1 ряд сходится; 2) l
=1 необходимы дополнительные исследования;
3) l
>1 ряд расходится.
Признак
Коши(радикальный): если для членов
знакоположительного ряда ∑an
существует конечный предел n→∞
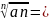 ℓ,то
при: 1) 0 ≤ l
<1 ряд сходится; 2) l
=1 необходимы дополнительные исследования;
3) l
>1 ряд расходится. Интегральный
признак: пусть члены знакоположительного
ряда ∑an
не возрастают,
а функция f (x) , определенная для x ≥1,
является непрерывной и невозрастающей,
причем f(1)=а1,
f (2) = a2,
…, f (n) = an,
… Тогда для сходимости ряда ∑an
необходимо
и достаточно, чтобы сходился несобственный
интеграл (от 1 до ∞)∫f(x)dx.
40.
Знакопеременные
и знакочередующиеся ряды. Абсолютная
и условная сходимость. Признак Лейбница.
ℓ,то
при: 1) 0 ≤ l
<1 ряд сходится; 2) l
=1 необходимы дополнительные исследования;
3) l
>1 ряд расходится. Интегральный
признак: пусть члены знакоположительного
ряда ∑an
не возрастают,
а функция f (x) , определенная для x ≥1,
является непрерывной и невозрастающей,
причем f(1)=а1,
f (2) = a2,
…, f (n) = an,
… Тогда для сходимости ряда ∑an
необходимо
и достаточно, чтобы сходился несобственный
интеграл (от 1 до ∞)∫f(x)dx.
40.
Знакопеременные
и знакочередующиеся ряды. Абсолютная
и условная сходимость. Признак Лейбница.
a1
+ a2
+…+an…=∑an(1)
– называется
знакопеременным, если его членами
являются действительные числа
произвольного знака. Если сходится
ряд |a1|
+ |a2
|+…+|an|…=∑|an|
(2), то ряд (1) называется абсолютно
сходящимся. Если ряд (1) сходится, а ряд
(2) расходится, то ряд (1) называется
условно сходящимся. Если знакопеременный
ряд сходится абсолютно, то он остается
абсолютно сходящимся при любой
перестановке его членов. При этом сумма
ряда не зависит от порядка его членов.
![]()
Это знакочередующийся рад(3). Признак Лейбница: если для знакочередующегося ряда (3) выполнены условия: 1) a1 ≥ a2 ≥ ... ≥ an ≥ an+1 ≥ ...; 2) предел an→0, то данный ряд сходится, а его сумма не превышает первого члена ряда. 41. Степенной ряд, его определение. Сходимость степенных рядов. Теорема Абеля. Св-ва степенных рядов.
Степенным рядом называют ряд вида c0 +c1x+c2 x2+…+cn xn…= (n=0 до ∞)∑cn xn, где c0, c1, c2,... – действительные числа, называемые коэффициентами ряда. Совокупность значений x∈ℝ, при которых степенной ряд сходится, называется областью сходимости этого ряда. Ряд называется абсолютно сходящимся, если сходится ряд ∑|cn xn|. Теорема Абеля: eсли степенной ряд сходится при x = x0, то он сходится абсолютно при всех x, удовлетворяющих условию
|x|< |x0|. Если ряд расходится при x = x1, то он расходится при всех x, удовлетворяющих условию |x |> |x1|. Св-ва: Если функция f (x) на интервале (−R, R) является суммой ряда f(x)=c0 +c1x+c2 x2+…+cn xn…, то она дифференцируема на этом интервале и ее про-изводная f ′(x) находится почленным дифференцированием ряда , т.е. f’(x)=c1 +2c1x+c2 x+…+ncn xn-1… при этом радиус сходимости полученного ряда равен R. Степенной ряд можно почленно интегрировать на любом отрезке, целиком принадлежащем интервалу сходимости, при этом полученный степенной ряд имеет тот же радиус сходимости, что и исходный ряд.
42. Нах-ие радиуса и интервала сх-ти степенных рядов.
Радиусом сходимости степенного ряда c0 +c1x+c2 x2+…+cn xn…= (n=0 до ∞)∑cn xn называется неотрицательное число R, такое, что при x < R ряд сходится, а при x > R – расходится. Интервалом сходимости называется интервал
(−R,R). Для выражения
радиуса сходимости степенного ряда
через его коэффициенты можно
использовать признак Д'Аламбера или
признак Коши.
Если
существует конечный предел
![]() то радиус сходимости ряда равен
то радиус сходимости ряда равен
![]() Если
существует конечный предел
Если
существует конечный предел
![]() то радиус сходимости ряда равен
то радиус сходимости ряда равен
![]()
Формулами этими выражается и радиус сходимости ряда, интервалом сходимости этого ряда является интервал (x0 − R, x0 + R).
43. Ряды Тейлора и Маклорена.
f(x0)
+ f’(x0)(x-x0)
+
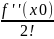 (x-x0)2
+…+
(x-x0)2
+…+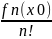 (x-x0)n+…=(от
0 до ∞)∑
(x-x0)n+…=(от
0 до ∞)∑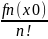 (x-x0)n,
называется рядом Тейлора функции f
(x)
в точке x0.
Если
x0 = 0, то ряд f(0) +
(x-x0)n,
называется рядом Тейлора функции f
(x)
в точке x0.
Если
x0 = 0, то ряд f(0) +
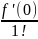 x
+
x
+
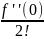 x2
+…+
x2
+…+
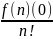 xn…=∑
xn,
называется рядом Маклорена.
Ряд
Тейлора, составленный для функции f
(x)
, как всякий степенной ряд, будет иметь
интервал сходимости и сумму, причем
сумма может быть и не равной f
(x)
.
xn…=∑
xn,
называется рядом Маклорена.
Ряд
Тейлора, составленный для функции f
(x)
, как всякий степенной ряд, будет иметь
интервал сходимости и сумму, причем
сумма может быть и не равной f
(x)
.
