
- •Вопрос1
- •1.Матрицы и линейные действия с ними. Свойства линейных операций с матрицами.
- •Вопрос2
- •3.Перестановки n чисел, их свойства, четные и нечетные перестановки, транспозиции.
- •Вопрос3 Определитель.
- •Вопрос1
- •Вопрос2
- •Вопрос3
- •Критерий совместимости системы лау. Теорема Кронекера-Копелли.
- •Вопрос4
- •Вопрос5
- •Вопрос1.
- •Вопрос2
- •Вопрос3
- •Вопрос4
- •Вопрос5
- •Вопрос1Евклидовы пространства. Определения и примеры.
- •Вопрос2
- •Вопрос1
- •Вопрос3 Матрицей оператора в базисе называется квадратная матрица порядка n, в j - том столбце которой стоят координаты вектора в базисе .
- •Вопрос4
- •Вопрос1
- •Вопрос3
- •Вопрос4
- •Вопрос3
Вопрос2
Ортогональное дополнение мн-ва.теорема о разлож.унит.пр-ва в прямую сумму подпр-ва.
Def:
Два подпространства
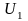 и
и
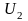 унитарного (евклидова) пространства
называется ортогональными
унитарного (евклидова) пространства
называется ортогональными
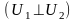 ,
если
,
если
 :
:
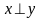 или
или
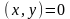
Lem
1: Если
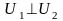 ,
то
,
то
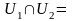 {θ}
{θ}
Док-во:
Пусть
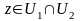 ,
т.е.
,
т.е.
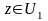 и
и
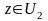 ,
т.к.
,
то
,
т.к.
,
то
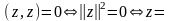 θ #
θ #
Пусть
─ подпространство пространства
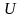 (
(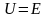 или
или
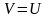 ).
#
).
#
Def:
Ортогональн доп-ем
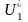 подпр-ва
пр-ва
подпр-ва
пр-ва
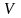 наз-ся множ-во всех векторов, ортогональных
подпр-ву
,т.е.
=
наз-ся множ-во всех векторов, ортогональных
подпр-ву
,т.е.
=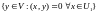
Пример: V-пространство всех геометрических (свободных) векторов
-подпространство всех векторов параллельных некоторой плоскости
─ подпространство всех векторов, перпендикулярных данной плоскости.
Утв::
Ортогональное дополнение произвольного подпространства пр-ва V само является подпространством данного пространства
Док-во:
В самом деле,

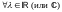 :
:
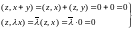
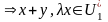 #
#
Lem
2 (критерий): ]
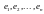 ─ базис в подпространстве
.
Вектор
─ базис в подпространстве
.
Вектор
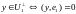 ;
;
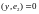 ,
…,
,
…,
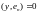
Док-во:
Необходимость: Пусть
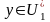 ,
тогда
,
тогда
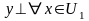 в том числе
в том числе
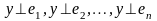 .
.
Достаточность:
 Пусть
Пусть
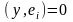
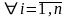 ,
поскольку
,
поскольку
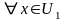 :
:
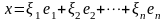 ,
то
,
то
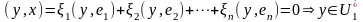 #
#
Th:
Унитарное
(евклидово) пространство
есть прямая сумма произвольного
подпространства
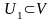 и его ортогонального дополнения
,
т.е.
и его ортогонального дополнения
,
т.е.
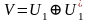 (прямая сумма)
(прямая сумма)
Док-во:
Пусть ── ОНБ в подпространстве .
Возьмем
произвольный в-р
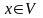 и сопоставим следующий в-р:
и сопоставим следующий в-р:
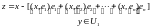
имеем
(скалярное умножение на
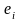 ):
):
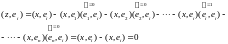
следовательно по Лемме 2
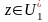 ,
т.е.
,
т.е.
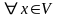 :
:
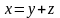 ,
где
,
где
 ,
,
![]()
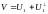 .
Но
.
Но
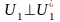
следовательно по Лемме 1
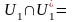 {θ},
откуда
по определению прямой суммы вытекает,
что
#
{θ},
откуда
по определению прямой суммы вытекает,
что
#
Следствие 1:
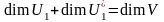
Док-во:
Доказательство следует из теоремы 2 §
5 гл. III (Пусть V – сумма подпространств
V1 и V2, тогда
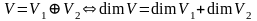 )
#
)
#
Вопрос1
Определение линейного оператора. Простейшие свойства. Примеры. Действия с линейными операторами и их свойства.
V – некоторое линейное пространство. L(V) – множество всех линейных операторов, действующих в пространстве V.
[О.1]: Оператором (преобразованием, отображением) линейного пространства V называется закон, по которому каждому элементу этого пространства xÎV ставится в соответствие единственный элемент из того же самого пространства yÎV. Будем обозначать операторы буквами A,B,C…
Ax=y; x-прообраз элемента y; y=Ax – образ элемента x (результат действия оператора).
[О.2]: оператор А, действующий в V, называется линейным, если выполняется следующие условия:
1) "x,yÎV: A(x+y)=Ax+Ay
2) "xÎV,"l: A(lx)=lAx
Простейшие свойства:
1° A(0)=0, где А-линейный оператор.
[Док-во]: пусть хÎV, тогда 0=0x A(0)=A(0x)=0(Ax)=0
2° Линейный оператор переводит противоположенный в противоположенный: A(-x)=-Ax
[Док-во]: "xÎV: А(-x)=A((-1)x)=(-1)Ax=-Ax
3° "x1,…,xkÎV, "l1,…,lk A(l1x1+…+lkxk)=l1Ax1+…+lkAxk.
4° Если система векторов x1,…,xk линейно зависима, то система образов так же линейно зависима, т.е существуют l1,…,lk такие, (не все равные нулю), что l1x1+…+lkxk=0
[Док-во]: A(l1x1+…+lkxk)=A0=0=> l1Ax1+…+lkAxk=0 => т.к. |l1|+…+|lk|¹0 Ax1+…+Axk линейно зависимы.
[О.3]: пусть А и В линейные операторы в V 1) A=B (A равен В), если "xÎV:Ax=Bx 2) Оператор I называется тождественным (или единичным), если "xÎV: Ix=x
3) O–нулевой оператор, если "хÎV: Ox=0.
Действия с линейными операторами.
[О.4]: 1) Суммой линейных операторов A,BÎL(V) называется оператор A+B, такой, что "хÎV: (А+В)х=Ах+Вх. 2) Произведением оператора А на l называется оператор lА, такой, что "хÎV: (lА)x=l(Аx)
[Теорема]: Множество L(V) является линейным пространством.
[Док-во]:
а)"x,yÎV:
(A+B)(x+y)=A(x+y)+B(x+y)=Ax+Ay+By+Bx=(Ax+Bx)+(Ay+By)=(A+B)x+(A+B)y.
б) "l: (A+B)(lx)=A(lx)+B(lx)=l(Ax+Bx)=l(A+B)x => L(V) – линейное пространство.
[О.5]: Произведением линейных оператором А,ВÎL(V) называется оператор АВ, такой, что "xÎV: (AB)x=A(Bx).
[Теорема]: Если A,BÎL(V), то (AB)ÎL(V)
[Док-во]: а)"x,yÎV AB(x+y)=A(B(x+y))=A(Bx+By)=A(Bx)+A(By)=(AB)x+(AB)y
б) "l: (AB)(lx)=A(Blx)=A(lBx)=l(A(Bx))=l(AB)x=>AB – линейный оператор.
Свойства:
1° (AB)C=A(BC)
[Док-во]: "XÎV ((AB)C)x=(AB)(Cx)=(A(B(Cx)))=A((BC)x)=(A(BC))x=>(AB)C=A(BC)
2° A(B+C)=AB+AC
[Док-во]: (A(B+C))x=A((B+C)x)=A(Bx+Cx)=A(Bx)+A(Cx)=(AB)x+(AC)x=(AB+AC)x=>A(B+C)= AB+AC.
3° (B+C)A=BA+CA
4° (lA)B=A(lB)=l(AB)
5° A0=0 6° AI=IA=A
Определение
9. Ядром линейного оператора называется
множество всех векторов
![]() .
Ядро оператора A
будем обозначать Ker A.
.
Ядро оператора A
будем обозначать Ker A.
![]() .
Дефектом
линейного оператора
называется размерность его ядра. Дефект
оператора будем обозначать Def A
= dim Ker A
.
Дефектом
линейного оператора
называется размерность его ядра. Дефект
оператора будем обозначать Def A
= dim Ker A
Образом
линейного оператора
называется множество всех векторов
![]() ,
таких что найдется
,
таких что найдется
![]() (то есть все множество образов) .
Образ
оператора A
будем обозначать Im
A
.
(то есть все множество образов) .
Образ
оператора A
будем обозначать Im
A
.
![]() .
.
Рангом линейного оператора называется размерность его образа .
Вопрос2 Обратный оператор для данного линейного оператора и его свойства. Критерий обратимости линейного оператора. Критерий обратимости линейного оператора. Матрица обратного оператора. Примеры обратимых и необратимых операторов.
Пусть V-линейное пространство, AÎL(V).
[О.1]: Множество всех векторов хÎV таких, что Ax=0, называется ядром оператора А: kerA=det{xÎV, Ax=0}. Множество всех векторов yÎV таких, что найдётся xÎV; y=Ax, называется образом оператора А, т.е. образ оператора А- это все элементы V такие, что ImA={yÎV:$xÎV, y=Ax}
[Теорема]: Ядро и образ линейного оператора AÎL(V) являются подпространством линейного пространства V.
[О.2]: Пусть V-линейное пространство и VÎL(V). Оператор А называется обратимым, если существует оператор В такой, что АВ=ВА=I. Если А-обратим, то A-1=B называют обратным к А.
Свойства обратного оператора:
1° Если у А существует обратный оператор, то он линейный.
[Док-во]: а)А-1(х+у)=А-1(Ix+Iy)=A-1((AA-1)x+(AA-1)y)=A-1(A(A-1x)+A(A-1)y))=A-1(A(A-1x+A-1y))=(A-1A)(A-1x+A-1y)=A-1x+A-1y
б) A-1(lx)=A-1(l(AA-1)x)=A-1(lA(A-1x))=A-1(A(lA-1x))=lA-1x=>A-1ÎL(V)
2° Если у А существует обратный оператор, то он единственный.
[Док-во]: Пусть существует B: AB=BA=I. A-1=A-1I=A-1(AB)=(A-1A)B=IB=B
3° Если оператор обратим, то его ядро равно нулевому элементу.
[Док-во]: Пусть хÎkerA: х=Ix=(A-1A)x=A-1(Ax)=A-1(0)=0
4° Если оператор обратим, то образ оператора тождественен V.
[Док-во]: "yÎV: y=Iy=(AA-1)y=A(A-1y)=AxÎImA. A-1y=x
[Теорема]: Критерий обратимости. AÎL(Vn) обратим тогда и только тогда, когда он невырожденный (т.е. detA¹
[Док-во]: 1) Пусть А-обратим, тогда существует A-1ÎL(Vn) АA-1=A-1А=I. Зафиксируем базис [e]= (e1,…,en) в Vn. [e]: A<->Ae, A-1<->(A-1)e, J<->E – единичная матрица. т.к. АA-1= A-1А=I, то Ae(A-1)e=(A-1)eAe=E=>detAe¹0, т.е. А-невырожденный => (A-1)e=Ae-1 2)Пусть detA¹0, тогда [e]: A<->Ae detA=detAe¹0=>матрица имеет обратную Ae-1. В базисе [e] существует BÎL(Vn): Be=Ae-1. AeAe-1= Ae-1Ae=E <-> AB=BA=J=>оператор B обратим к оператору А В=A-1;Be=Ae-1.
