
- •27. 28. 29. Правила обчислення похідної:
- •40. 40. Первісна. Теорема про загальний вигляд первісної
- •41. Означення невизначеного інтеграла
- •42. Основні властивості невизначеного інтеграла
- •55.Диференціальні рівняння 1-го порядку:основні поняття та означення.Задача Коші
- •56. Диференціальні рівняння з відокремлюваними змінними
- •57. Однорідні диференціальні рівняння першого порядку
- •58. Лінійні диференціальні рівняння першого порядку
40. 40. Первісна. Теорема про загальний вигляд первісної
Функція F(x)зветься первісною функції f(x) на деякому інтервалі дійсних чисел, якщо f(x) — похідна функції F(x) на цьому інтервалі, тобто в усіх внутрішніх точках інтервалу виконується рівність
F’(x)=f(x). Можна довести, що у будь-якої неперервної на інтервалі функції f(x) існує первісна, яка також є неперервною функцією на цьому інтервалі.
Якщо F(x) — будь-яка первісна функція f(x) то F(x)+C, де C - довільна стала, — також первісна цієї функції і "невизначений інтеграл функції f(x)" посилається до множини {F(x) + C|C є R}, яка складається з усіх первісних функції f(x) де C — довільна константа
Теорема про загальний вигляд первісної: Якщо функція F(x) первісна для функції f(x), то для того щоб функція Ф(x) була первісною для функції f(x) необхідно і достатньо, щоб вона відрізнялася від F(x) на const. Ф(x) = F(x) + C – загальний вигляд первісної.
Загальний вигляд первісної для функції f(x) називається невизначеним інтегралом функції f(x).
41. Означення невизначеного інтеграла
Загальний вигляд первісної для функції f(x) називається невизначеним інтегралом функції f(x).З точки зору геометрії невизначений інтеграл функції представляє собою множину (сім’ю) кривих кожна з яких називається інтегральною кривою і утворюється із іншої внаслідок паралельного перенесення вздовж осі Оу на const (c).
42. Основні властивості невизначеного інтеграла
Властивості невизначеного інтеграла:
Похідна невизначеного інтеграла дорівнює підінтегральній функції:
Невизначений інтеграл від диференціала деякої функції дорівнює сумі цієї функції і довільної сталої:
Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу:
Сталий множник можна виносити за знак інтеграла:
Невизначений інтеграл від алгебраїчної суми двох функцій дорівнює алгебраїчній сумі інтегралів від цих функцій:
Якщо
 і
і
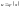 - довільна функція, що має неперервну
похідну, то
- довільна функція, що має неперервну
похідну, то
 .
.
43. Основні методи інтегрування
Метод безпосереднього інтегрування
Обчислення інтегралів за допомогою основних властивостей невизначеного інтеграла і таблиці інтегралів називається безпосереднім інтегруванням.
Метод підстановки (заміни змінної)
Суть цього методу полягає у введенні нової змінної інтегрування.
Метод інтегрування частинами
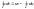 .
.
44.Задача про площу криволінійної трапеції. Означення та умови існування визначеного інтеграла
Нехай
на відрізку
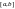 задано функцію
задано функцію
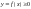 .
Фігура, обмежена графіком даної функції
і відрізками прямих
.
Фігура, обмежена графіком даної функції
і відрізками прямих
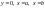 ,
називається криволінійною
трапецією.
Обчислимо площу цієї трапеції.
Розіб’ємо
відрізок
,
називається криволінійною
трапецією.
Обчислимо площу цієї трапеції.
Розіб’ємо
відрізок
 на
на
 довільних частин точками:
довільних частин точками:
 .
Сукупність
точок
.
Сукупність
точок
 позначимо через Т і назвемо Т–розбиттям
відрізка
позначимо через Т і назвемо Т–розбиттям
відрізка
 .
На
кожному частинному відрізку
.
На
кожному частинному відрізку
 ,
візьмемо довільну точку
,
візьмемо довільну точку
 і обчислимо значення
і обчислимо значення
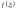 .
Тоді добуток
.
Тоді добуток
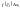 ,
де
,
де
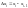 - довжина відрізка
- довжина відрізка
 дорівнює площі прямокутника з основою
дорівнює площі прямокутника з основою
 і висотою
,
а сума цих добутків
і висотою
,
а сума цих добутків
 –
площа ступінчатої фігури і наближено
дорівнює площі криволінійної трапеції:
–
площа ступінчатої фігури і наближено
дорівнює площі криволінійної трапеції: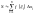 .
Сума (1) називається інтегральною
сумою функції
.
Сума (1) називається інтегральною
сумою функції
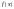 ,
яка відповідає Т-розбиттю відрізка
на частинні відрізки і даному вибору
точок
,
яка відповідає Т-розбиттю відрізка
на частинні відрізки і даному вибору
точок
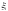 .Із
зменшенням усіх величин
.Із
зменшенням усіх величин
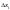 точність формули (2) збільшується, тому
природно за площу криволінійної трапеції
вважати границю площ ступінчатих фігур
за умови, що максимальна довжина
частинних відрізків прямує до нуля:
точність формули (2) збільшується, тому
природно за площу криволінійної трапеції
вважати границю площ ступінчатих фігур
за умови, що максимальна довжина
частинних відрізків прямує до нуля:
 .Якщо
існує скінченна границя інтегральної
суми (1) при
.Якщо
існує скінченна границя інтегральної
суми (1) при
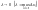 ,
яка не залежить ні від Т–розбиття, ні
від вибору точок
,
яка не залежить ні від Т–розбиття, ні
від вибору точок
 ,
то ця границя називається визначеним
інтегралом
функції
на відрізку
,
то ця границя називається визначеним
інтегралом
функції
на відрізку
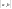 і позначається символом
і позначається символом
 .Отже,
згідно з означенням:
.Отже,
згідно з означенням:  .Функція
.Функція
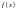 називається інтегрованою
на відрізку
називається інтегрованою
на відрізку
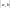 .
Числа
.
Числа
 називаються відповідно нижньою
і верхньою
межею інтегрування;
функція
називаються відповідно нижньою
і верхньою
межею інтегрування;
функція
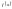 називається підінтегральною
функцією;
називається підінтегральною
функцією;
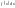 – підінтегральним
виразом;
– підінтегральним
виразом;
 – змінною інтегрування;
– змінною інтегрування;
 – проміжком
інтегрування.
Площа криволінійної трапеції, обмеженої
прямими
– проміжком
інтегрування.
Площа криволінійної трапеції, обмеженої
прямими
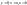 і
графіком функції
і
графіком функції
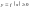 ,
дорівнює визначеному інтегралу від
цієї функції
,
дорівнює визначеному інтегралу від
цієї функції
 .
У цьому полягає геометричний зміст
визначеного інтеграла: визначений
інтеграл від невід’ємної функції
чисельно дорівнює площі відповідної
криволінійної трапеції.
.
У цьому полягає геометричний зміст
визначеного інтеграла: визначений
інтеграл від невід’ємної функції
чисельно дорівнює площі відповідної
криволінійної трапеції.
45.Якщо
існує скінченна границя інтегральної
суми (1) при
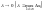 ,
яка не залежить ні від Т–розбиття, ні
від вибору точок
,
яка не залежить ні від Т–розбиття, ні
від вибору точок
 ,
то ця границя називається визначеним
інтегралом
функції
на відрізку
,
то ця границя називається визначеним
інтегралом
функції
на відрізку
 і позначається символом
і позначається символом
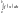 .
Площа криволінійної трапеції, обмеженої
прямими
.
Площа криволінійної трапеції, обмеженої
прямими
 і
графіком функції
і
графіком функції
 ,
дорівнює визначеному інтегралу від
цієї функції
,
дорівнює визначеному інтегралу від
цієї функції
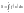 .
У цьому полягає геометричний зміст
визначеного інтеграла: визначений
інтеграл від невід’ємної функції
чисельно дорівнює площі відповідної
криволінійної трапеції.
.
У цьому полягає геометричний зміст
визначеного інтеграла: визначений
інтеграл від невід’ємної функції
чисельно дорівнює площі відповідної
криволінійної трапеції.
