1. Визначник не зміниться, якщо його рядки замінити відповідними стовпцями.Якщо переставити місцями два рядки (стовпці), то визначник поміняє знакЯкщо один з рядків (стовпців) визначника складається тільки з нулів, то визначник дорівнює нулю.Якщо визначник має два однакових рядки (стовпці), то він дорівнює нулю.Спільний множник, що мітиться в усіх елементах одного рядка (стовпця), можна винести за знак визначника.Якщо у визначнику елементи двох рядків (стовпців) пропорційні, то визначник дорівнює нулю.Якщо кожен елемент рядка ( стовпця) є сума двох доданків, то такий визначник дорівнює сумі двох визначників, у одного з яких рядок ( стовпець) складається з перших доданків, а у другого – з других; інші елементи усіх трьох визначників однакові.Визначник не зміниться, якщо до елементів одного рядка (стовпця) додати відповідні елементи іншого рядка (стовпця), помножені на одне й те саме число.

2. Мінором елемента визначника називається визначник, який утворюється з даного визначника викресленням рядка та стовпця.Алгебраїчним доповненням елемента називається його мінор, взятий зі знаком , тобто .

3. Теорема 1.Визначник дорівнює сумі добутків елементів якого-небудь рядка (стовпця) на їхні алгебраїчні доповнення.

Для визначника (3) виконуються такі рівності:

2. Теорема 2. Сума добутків будь-якого рядка (стовпця) визначника на алгебраїчні доповнення відповідних елементів іншого рядка (стовпця) дорівнює нулю.

3. Визначник п-го порядку дорівнює сумі добутків елементів будь-якого рядка (стовпця) на їхні алгебраїчні доповнення. Всі розглянуті вище властивості визначників третього порядку справджуються для визначників будь-якого порядку., Прямокутна таблиця чисел 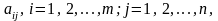складена з т рядків та п стовпців називається матрицею. Добуток числа рядків т на число стовпців п називають розміром матриці і позначають _ь*т. Записують розмір матриці: Матриця, в якої число рядків дорівнює числу стовпців, називається квадратною. Кількість рядків (стовпців) квадратної матриці називається її порядком. Матриця, у якої всього один рядок, називається матрицею-рядком, а матриця, у якої всього один стовпець, матрицею-стовпцем.

Дві матриці та називаються рівними, якщо вони однакових розмірів і мають рівні відповідні елементи: Нульовою називається матриця, у якої всі елементи дорівнюють нулю. Позначається така матриця буквою О. В квадратних матрицях виділяють головну і побічну діагональ. Квадратна матриця називається діагональною, якщо всі її елементи, крім тих, що знаходяться на головній діагоналі, дорівнюють нулю.

Діагональна матриця, у якої кожен елемент головної діагоналі дорівнює одиниці, називається одиничною і позначається буквою Е. Будь-якій квадратній матриці

можна поставити у відповідність певне число, яке називається визначником (детермінантом) цієї матриці і позначається символом det A. За означенням

Прямокутна матриця розміром визначника не має.

2. Операція додавання матриць вводиться тільки для матриць однакового розміру. Сумою С = А + В двох матриць називається матриця

Добутком матриці на число К (або число К на матрицю називається матриця .Різниця матриць А – В визначається як сума матриць А і матриці В, помноженої на -1:

Властивості операцій:

Операція множення двох матриць вводиться лише для узгоджених матриць. Матриця А називається узгодженою з матрицею В, якщо кількість стовпців першої матриці А дорівнює кількості рядків другої матриці В. Операція множення матриць не комутативна, тобто при множені матриць не можна міняти місцями множники: _Добутком С = АВ матриці на матрицю називається така матриця, у якої елемент дорівнює сумі добутків елементів і-го рядка матриці А на відповідні елементи j-го стовпця матриці В:Нехай А – квадратна матриця. Матриця називається оберненою до матриці А, якщо виконується умова: Квадратна матриця А називається виродженою, якщо і невиродженою, якщо Теорема.Для існування оберненої матриці необхідно і достатньо, щоб матриця А була невиродженою.

2. Системою т лінійних рівнянь з п невідомими х₁, х₂, ..., х_п називається система виду

Числа біля невідомих називаються коефіцієнтами, а числа - вільними членами системи. Система рівнянь називається однорідною, якщо всі вільні члени дорівнюють нулю, і неоднорідною, якщо хоч один з них відмінний від нуля. Множина чисел називається впорядкованою, якщо вказано порядок слідування цих чисел, тобто вказано, яке з них є першим, яке другим, яке третім і т.д. Система рівнянь називається сумісною, якщо вона має хоча б один розв’язок, і несумісною, якщо вона не має жодного розв’язку.

Сумісна система називається невизначеною, якщо вона має більше, ніж один розв’язок.

Дві системи лінійних рівнянь називаються еквівалентними, якщо вони мають одну й ту ж множину розв’язків.

2. Якщо визначник системи то система має єдиний розв’язок, який знаходиться за формулами Крамера:

1) тоді система має єдиний розв’язок: 2) або тоді система не має розв’язків.

3) тоді система зводиться до одного рівняння і має безліч розв’язків, тобто невизначеною.

2. Матрицю А, складену з коефіцієнтів системи називають основою матрицею системи, матрицю Х – матрицею з невідомих, а матрицю В – матрицею з вільних членів. Тоді згідно з правилом множення матриць систему можна записати одним матричним рівнянням з невідомою матрицею Х: АХ=В. Припустимо, що матриця А системи має обернену матрицю А^-1; помножимо обидві частини рівності на А^-1 зліва: А^-1АХ=А^-1В.

Оскільки А^-1А=Е і ЕХ=Х, ТО Х=А^-1В

Отже, щоб розв’язати систему рівнянь (8), достатньо знайти матрицю, обернену до матриці системи, і помножити її справа на матрицю з вільних членів.

Формулу (11) називають матричним записом розв’язку системи або розв’язком матричного рівняння

2. Визначник порядку _К, складений з елементів, що стоять на перетині виділених рядків і стовпців, називається мінором _К-го порядку матриці А.Рангом r(А) матриці А називається найбільший з порядків її мінорів, відмінних від нуля.Безпосередньо з означення випливає, що:

1. Ранг існує для будь-якої матриці , причому 2) тоді і тільки тоді, коли А = 0;

3) Для квадратної матриці п-го порядку ранг дорівнює п тоді і тільки тоді, коли матриця невироджена.

Правило знаходження рангу матриці: Якщо всі мінори першого порядку (елементи матриці) дорівнюють нулю, то . Якщо хоч один з мінорів першого порядку відмінний від нуля, а всі мінори другого порядку дорівнюють нулю то .У випадку, коли є мінор другого порядку, відмінний від нуля, досліджуємо мінори третього порядку. Так продовжуємо доти, поки не станеться одне з двох: або всі мінори порядку дорівнюють нулю, або мінорів порядку _К не існує, тоді .

2. При розв’язуванні системи лінійних рівнянь методом Гауса зручніше приводити до трикутного чи трапецієподібного вигляду не саму систему рівнянь, а розширену матрицю цієї системи, тобто матрицю, утворену приєднанням до матриці її коефіцієнтів стовпця вільних членів. Виконуючи над рядками розширеної матриці елементарні перетворення, приходимо до розв’язку системи.

3. 14.

• – загальне рівняння прямої;

• – рівняння прямої, що проходить через точку перпендикулярно до нормального вектора ;

• – рівняння прямої, що проходить через точку паралельно напрямному вектору (канонічне рівняння прямої) ;

• , – параметричні рівняння прямої, що у векторній формі мають вигляд ;

• – рівняння прямої у відрізках на осях, де a і b – відрізки, що їх відтинає пряма на координатних осях Ох та Оy відповідно;

• – рівняння прямої з кутовим коефіцієнтом, де _К – кутовий коефіцієнт прямої, , - величина відрізка, що його відтинає пряма на осі Оy;

• – рівняння прямої, що проходить через задану точку і має заданий кутовий коефіцієнт;

• – нормальне рівняння прямої, де – довжина перпендикуляра, проведеного з початку координат на пряму, – кут нахилу цього перпендикуляру до осі Ох.

15. Рівняння називається загальним рівнянням прямої на площині, де – координати вектора нормалі до прямої, – вільний член.

1. Рівняння визначає пряму, що проходить через початок координат;

2. Рівняння або визначає пряму, паралельну Оу;

3. Рівняння або визначає пряму, паралельну Ох;

4. Рівняння або визначає вісь Оу;

5. Рівняння або визначає вісь Ох;

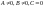6. Рівняння визначає пряму .

Пряма 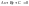ділить площину на дві півплощини так, що для координат точок однієї з них справджується нерівність , а для координат іншої – нерівність .

15. Кутом між прямими l₁ і l₂ називається кут , на який треба повернути пряму l₁ (проти годинникової стрілки), щоб вона сумістилась з прямою l₂.

І. Якщо прямі задано канонічними рівняннями 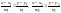, то кут між прямими знаходиться за формулою .

Умова паралельності: .

Умова перпендикулярності: .

ІІ. Якщо прямі задано рівняннями з кутовими коефіцієнтами 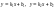, то .

Умова паралельності: . Умова перпендикулярності: .

ІІІ. Якщо прямі задано загальними рівняннями , то .

Умова паралельності: . Умова перпендикулярності: .

Відстань від точки до прямої знаходиться за формулою .

15. Колом називається множина точок площини, відстань яких від заданої точки площини (центра кола) дорівнює сталому числу (радіусу).

(1) - рівняння кола з центром в точці .

Якщо центр кола міститься в початку координат, то і рівняння кола набуває вигляду (2). Це канонічне рівняння кола.

Якщо розкрити дужки у рівнянні, то отримаємо загальне рівняння кола: .

Рівняння кола має такі властивості:Коефіцієнти при х² та y² рівні між собою;У рівнянні відсутній член з добутком хy.

15. 19. Еліпсом називається множина всіх точок площини, сума відстаней яких від двох даних точок цієї площини, які називаються фокусами, є величина стала, і більша від відстані між фокусами.

Відстань між фокусами позначимо, 2С а суму відстаней від довільної точки еліпса до фокусів через 2Ф. Тоді за означенням , тобто 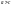. Позначимо .

Канонічне рівняння еліпса .

Еліпс перетинає осі координат в точках . Ці точки називаються вершинами еліпса.

Величини називаються відповідно великою та малою осями еліпса.

Ексцентриситет еліпса дорівнює відношенню половини його фокальної відстані до довжини більшої півосі , причому . Рівняння дотичної до еліпса у точці має вигляд .

Еліпс з центром у точці задається рівнянням . Прямі називаються директрисами еліпса.

Відстані F₁M=r₁ та F₂M=r₂ називаються фокальними радіусами точки М; r₁+r₂=2a.

Відношення фокальних радіусів довільної точки еліпса до відстаней цієї точки від відповідних директрис є величина стала і дорівнює ексцентриситету еліпса, тобто .

20. 21. Гіперболою називається множина всіх точок площини, модуль різниці відстаней яких від двох даних точок цієї площини, що називаються фокусами, є величина стала і менша відстані між фокусами.

Канонічне рівняння гіперболи . Асимптоти гіперболи – це прямі, які задаються рівняннями . Осі симетрії називається осями гіперболи, а точка перетину осей – її центром. Вісь Ох перетинає гіперболу в двох точках , які називаються вершинами гіперболи. Ця вісь називається дійсною віссю гіперболи, а вісь, яка не має спільних точок з гіперболою – уявною віссю.

Дійсною віссю гіперболи називається також відрізок A₁A₂, який сполучає вершини гіперболи і його довжина дорівнює 2а. Відрізок В₁В₂, який сполучає точки , а також його довжину називають уявною віссю.

Величини a і b відповідно називають дійсною та уявною півосями гіперболи.

Прямокутник зі сторонами 2a і 2b називають основним прямокутником гіперболи.

Рівняння , яке також визначає гіперболу називають спряженою до гіперболи. Вершини цієї гіперболи лежать в точках , а її асимптоти збігаються з асимптотами гіперболи.

Гіпербола з рівними півосями (a=b), називається рівносторонньою, її канонічне рівняння має вигляд . Основним прямокутником рівносторонньої гіперболи є квадрат із стороною 2a, а її асимптоти – бісектриси координатних кутів.

Рівняння дотичної до гіперболи у точці має вигляд .Рівняння асимптот: .Гіпербола з центром у точці задається рівнянням .

22. 23. Параболою називається множина всіх точок площини, кожна з яких знаходиться на однаковій відстані від даної точки, яка називається фокусом, і від даної прямої, яка називається директрисою і не проходить через фокус.

Канонічне рівняння параболи .

Фокус має координати , рівняння директриси має вигляд .

Вісь симетрії параболи називається її віссю, точка перетину осі з параболою – вершиною параболи; число, яке дорівнює відстані фокуса від директриси, - параметром параболи.

Вісь параболи, заданої рівнянням , є вісь Ох, вершиною – точка О(0, 0) і параметром – число р. Параметр характеризує „ширину” області яку обмежує парабола.

Зауваження. Лінії другого порядку (крім кола) – це множина точок, для яких відношення відстані до фокуса і до відповідної директриси є величина стала, – це еліпс ( ), або парабола ( ), або гіпербола ( ).

24.25. Задачі, що приводять до поняття похідної: Задача про швидкість прямолінійного руху Задача про густину неоднорідного тіла Задача про силу струму Задача про теплоємність Задача про швидкість хімічної реакції Задача про дотичну до кривої

Похідною функції в точці називається границя відношення приросту функції в цій точці до приросту аргументу , коли приріст аргументу прямує до нуля.

Операція знаходження похідної від функції називається диференціюванням цієї функції.

Механічний зміст похідної: швидкість в даний момент часу – це похідна від пройденого шляху за часом .

Фізичний зміст похідної: якщо функція описує деякий фізичний процес, то похідна є швидкістю зміни цього процесу.

Геометричний зміст похідної: кутовий коефіцієнт дотичної до кривої в точці або тангенс кута , що утворює дотична до кривої в даній точці з додатним напрямом осі Ох – це похідна в цій точці: .

26. Довжина відрізка називається довжиною відрізка дотичної.

Довжина відрізка називається піддотичною.

Довжина відрізка називається довжиною відрізка нормалі.

Довжина відрізка називається піднормаллю.

Рівняння дотичної до кривої в точці : .

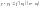Якщо функція в точці має нескінченну похідну, то дотична в цій точці паралельна осі Оу, а її рівняння .

Нормаллю до кривої називається пряма, що проходить через точку дотику, перпендикулярно до дотичної.

Рівняння нормалі до кривої в точці : .

27. 28. 29. Правила обчислення похідної:

1. 

2. (U*V)’=

31.

32.

33. Похідна показникової функції обчислюється за формулою:

. За основу логарифмічної тотожністю:

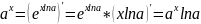
Похідна логарифмічної функції обчислюється за формулою: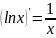

34. Якщо функція також має похідну на інтервалі або в деякій точці 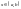, то її називають другою похідною (похідною другого порядку).

Механічний зміст похідної другого порядку: прискорення рухомої точки в даний момент часу.

Похідною порядку функції називають першу похідну, якщо вона існує від похідної порядку : .

Похідні порядку вище першого називають похідними вищого порядку.

Починаючи з похідної четвертого порядку, похідні позначають не штрихами, а цифрами. Порядок похідної береться в дужки.

35. Теорема 1 (достатні умови строгої монотонності)Якщо функція диференційовна на інтервалі і всюди, крім, можливо, скінченного числа точок, в яких на , то функція зростає (спадає).

Теорема 2 (необхідна умова зростання)Якщо диференційовна на інтервалі функція зростає, то на .

Інтервали монотонності можуть відділятись один від одного або точками, де похідна дорівнює нулю (їх називають стаціонарними точками), або точками, де похідна не існує.

Точки, в яких похідна дорівнює нулю або не існує називаються критичними точками першого роду.

Правило знаходження проміжків монотонності функції : Знайти область визначення функції;Знайти похідну функції;Знайти критичні токи з рівняння та з умови, що 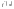не існує:розділити критичними точками область визначення на інтервали та у кожному з них визначити знак похідної. На інтервалах, де похідна додатна, функція зростає, а де від’ємна – спадає.

36. Точка називається точкою локального максимуму (мінімуму) функції , якщо існує такий окіл точки , який належить області визначення функції, і для всіх з цього околу виконується нерівність .

Точки локального максимуму і локального мінімуму називаються точками локального екстремуму, а значення функції в цих точках називаються відповідно локальним максимумом і локальним мінімумом або локальним екстремумом.

Абсолютний максимум (мінімум) – це найбільше (найменше) значення функції, яке вона може набувати в області визначення.

Локальних максимумів (мінімумів) функція може мати кілька, абсолютний максимум (мінімум) може бути тільки один.

Теорема 1 (необхідна умова локального екстремуму)Якщо функція 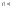має в точці локальний екстремум і диференційовна в цій точці, то .

Теорема 2 (перша достатня умова локального екстремуму)Нехай - критична точка функції , яка в цій точці неперервна, і нехай існує окіл точки , в якому функція має похідну крім, можливо, точки , тоді:

1. Якщо в інтервалі похідна , а в інтервалі похідна , то є точкою локального максимуму функції ;

2. Якщо в інтервалі похідна , а в інтервалі похідна , то є точкою локального мінімуму функції ;

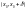3. Якщо в обох інтервалах і похідна має той самий знак, то не є екстремальною точкою функції .

Теорема 3 (друга достатня умова локального екстремуму)Нехай - стаціонарна точка функції , тобто , і в околі точки існує друга неперервна похідна, причому . Якщо , то - точка локального мінімуму; якщо , то - точка локального максимуму.

Теорема 4 (третя достатня умова локального екстремуму)

Нехай в околі стаціонарної точки існує неперервна похідна , причому , . Тоді:

1. якщо n – парне і , то має в точці локальний максимум;

2. якщо n – парне і , то має в точці локальний мінімум;

3. якщо n – непарне, то в точці локального екстремуму не має.

Нехай функція неперервна на відрізку 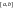. Така функція досягає своїх найбільшого і найменшого значень, які називаються абсолютними екстремумами функції на цьому відрізку і позначаються відповідно .

Правило знаходження найбільшого (найменшого) значення функції, неперервної на відрізку :

1. Знайти критичні точки функції , які належать інтервалу ;

2. Обчислити значення функції у знайдених критичних точках і точках А та В і серед цих значень вибрати найбільше (найменше).

37. 38. 39. Крива називається опуклою на інтервалі, якщо всі її точки, крім точки дотику, лежать нижче довільної її дотичної на цьому інтервалі.

Крива називається вгнутою на інтервалі, якщо всі її точки, крім точки дотику, лежать вище довільної її дотичної на цьому інтервалі.

Точкою перегину називається така очка кривої, яка відділяє її опуклу частину від вгнутої.

Теорема 1 (знаходження інтервалів опуклості і вгнутості)

Нехай функція є двічі диференційовною на 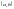, тоді:

1. якщо , то крива опукла на ;2. якщо , то крива вгнута на .

Наслідок. В точці перегину друга похідна дорівнює нулю (якщо вона існує).

Точки, в яких друга похідна дорівнює нулю або не існує, називаються критичними точками другого роду.

Теорема 2 (достатні умови існування точки розриву)

Нехай - критична точка другого роду функції . Якщо при переході через точку похідна змінює знак, то точка є точкою перегину кривої .

Наслідок. Щоб знайти точки перегину кривої треба знайти критичні точки другого роду і дослідити зміну знака другої похідної при переході через ці точки.

4. Асимптоти кривої

Пряма називається асимптотою кривої, якщо відстань від змінної точки кривої до цієї прямої прямує до нуля, коли точка,М рухаючись по кривій, віддаляється на нескінченність Для існування вертикальної асимптоти необхідно і достатньо, щоб , або , або .

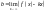Рівняння похилої асимптоти , де (1), (2).

Зауваження 1. Якщо хоча б одна з границь (1) або (2) не існує, або дорівнює нескінченності, то крива похилої асимптоти не має.

Зауваження 2. Якщо , то , тому – рівняння горизонтальної асимптоти.

Зауваження 3. Асимптоти кривої при і можуть бути різні. Тому при знаходженні асимптот границі (1) і (2) потрібно обчислювати при і .

Схема дослідження функції та побудова її графіка: Знайти область існування функції;

1. Знайти (якщо це можна) точки перетину графіка з координатними осями; дослідити функцію на періодичність, парність і непарність; знайти точки розриву і дослідити їх ; знайти інтервали монотонності, точки локальних екстремумів та значення функції в цих точках; знайти інтервали опуклості, вгнутості та точки перегину; знайти асимптоти кривої; побудувати графік функції.