
- •1.Ортогональные и ортонормированные системы функций, ряды Фурье по ортого-
- •§1 Ортогональные системы функций. Ряды Фурье по ортогональным системам функций
- •Частичные суммы рядов Фурье: ядро Дирихле, формулы Дирихле.
- •3.Сходимость ряда Фурье в точке: Принцип локализации, условие Гёльдера, теорема
- •4.Равномерная сходимость ряда Фурье: Неравенство Бесселя, Теорема о равномерной
- •5.Сходимость семейства функций: определение равномерной сходимости семейства
- •6.Собственные интегралы с параметрами: свойства, теорема о дифференцировании
- •§1. Собственные интегралы с параметрами
- •7. Равномерная сходимость несобственного интеграла с параметрами: определение,
- •8. Свойства равномерно сходящихся несобственных интегралов: теоремы о предель-
- •9. Свойства равномерно сходящихся несобственных интегралов: теоремы о диффе-
- •10. Эйлеровы интегралы. Гамма-функция: определение, основное соотношение, про-
- •§3. Эйлеровы интегралы
- •11. Интеграл Фурье: определение, теорема (с леммами) о сходимости интеграла Фу-
- •§4 Интеграл Фурье
- •12. Преобразование Фурье: определение, свойства (ограниченность и непрерывность
- •§5. Преобразования Фурье
- •13. Теоремы о преобразовании Фурье и дифференцировании. Преобразование Фурье
- •14. Системы множеств: определения кольца, минимального кольца. Теорема о сущест-
- •§1 Системы множеств
- •15. Мера клеточных множеств. Теорема о полуаддитивности меры клеточных мно-
- •16. Внешняя мера, измеримые множества, мера Лебега. Свойства внешней меры.
- •17. Теорема о конечной аддитивности меры Лебега. Теорема о счетной аддитивности
- •18. Теорема о непрерывности меры Лебега. Какие множества измеримы по Лебегу?
- •19. Обобщение понятие меры Лебега на случай всей плоскости. Пример неизмеримого
- •20.Мера Лебега-Стилтьеса. Понятие абсолютно-непрерывной, дискретной и сингу-
- •21. Общее понятие меры. Продоление меры. Теорема о существовании и единственно-
- •§3 Общее понятие меры
- •22. Лебегово продолжение меры. Структура системы измеримых по Лебегу множеств.
- •§4. Лебегово продолжение меры
- •23. Измеримые функции: определения (X,y ) – измеримой, -измеримой, борелев-
- •24. Теорема об арифметических операциях с измеримыми функциями. Теорема об из-
- •25.Понятие сходимости почти всюду. Теорема Егорова.
- •26. Понятие сходимости по мере. Две теоремы о связи сходимости по мере и сходимо-
- •27. Простые функции: определение, теорема о простой функции. Необходимое и дос-
- •28. Интеграл Лебега для произвольных функций. Свойства интеграла Лебега. Теорема
- •29. Предельный переход в интеграле Лебега. Теорема Лебега (с док-вом). Теоремы
- •30. Понятие сигма-конечной меры. Интеграл Лебега по множеству бесконечной меры.
- •31. Сравнение интеграла Лебега с интегралом Римана.
- •32. Произведение мер. Формула для нахождения меры множества с помощью интегра-
- •§ 7 Произведение мер. Теорема Фубини.
- •33. Пространства суммируемых функций l1 и l2 . Теорема о полноте пространства l1.
- •§ 8 Пространства суммируемых функций.
1.Ортогональные и ортонормированные системы функций, ряды Фурье по ортого-
нальным системам функций: определения, формулы для коэффициентов ряда Фу-
рье. Лемма Римана.
§1 Ортогональные системы функций. Ряды Фурье по ортогональным системам функций
П.1 Ортогональные системы функций
Пусть
 - множество (система) функций,
- множество (система) функций,
 ,
,
 ,
тогда
называется ортогональной
системой
,
если
,
тогда
называется ортогональной
системой
,
если
 (
( ):
):

Система
называется нормированной,
если
 .
.
Если выполняются оба условия, то система называется ортонормированной.
Примеры:
1, sin(x), cos(x), sin(2x), cos(2x) … sin(nx), cos(nx) … - ортогональна на [0, 2
 ]
или [-
,
].
]
или [-
,
].1,
 ,
,
 …
…
 ,
,
 …
- ортогональна
на [a,
b].
…
- ортогональна
на [a,
b].Многочлены Лежандра:
 -
ортогональная на [-1,
1].
-
ортогональная на [-1,
1].
П.2 Ряды Фурье по ортогональным системам функций
Пусть ортогональная система на [a,b],
 числовая
последовательность,
числовая
последовательность,
 .
.
Рассмотрим
 ,
пусть он сходится равномерно на [a,
b]
,
пусть он сходится равномерно на [a,
b]

 Лемма.
Пусть
Лемма.
Пусть
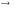
 равномерно на [a,
b],
тогда:
равномерно на [a,
b],
тогда: (*)
(*)
□
=

 =
= ,
,
 (т.к.
непрерывны на [a,
b])
(т.к.
непрерывны на [a,
b])
сходится
равномерно

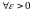 ,
,
 :
:

 ,
,
 . Тогда
. Тогда
 и
сходится
равномерно. Значит, его можно
проинтегрировать:
и
сходится
равномерно. Значит, его можно
проинтегрировать:
 ,
,
интеграл
в правой части равен нулю, при
 и
и
 ■
■
Пусть
произвольная функция. Если

 (*),
то рассмотрим
- ряд
Фурье
для функции
по ортогональной системе функций
.
Числа
(*),
то рассмотрим
- ряд
Фурье
для функции
по ортогональной системе функций
.
Числа
 ,
найденные по (*) называются коэффициентами
Фурье.
,
найденные по (*) называются коэффициентами
Фурье.
Если абсолютно интегрируема на [a, b], то найдется ряд Фурье для , но он может сходиться не к или вообще расходиться.
Пример:
 -
ортогональна на
-
ортогональна на
 ,
,

Обозначим

Тогда для коэффициентов Фурье справедливы формулы Фурье-Эйлера:

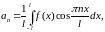

П.3 Лемма Римана
Пусть f(x) абсолютно интегрируема на [a, b] (конечный или бесконечный промежуток). Тогда:

Доказательство:
Пусть f(x) абсолютно интегрируема в собственном смысле, то есть
 -
интеграл Римана.
-
интеграл Римана.
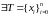 -
разбиение [a,
b]:
-
разбиение [a,
b]:
 ,
,
где
 ,
,
 ,
, ,
,
 .
.
Рассмотрим

Последнее неравенство верно, т.к.




 .
.
и
 - несобственные
- несобственные
Пусть
b
- особая точка. Тогда

 .
.

Аналогично
доказывается, что
 .
.
Частичные суммы рядов Фурье: ядро Дирихле, формулы Дирихле.
П.1 Частичные суммы рядов Фурье. Формула Дирихле.
Пусть
-
абсолютно интегрируемая на


 -
тригонометрический многочлен;
«2
»-периодическая
функция.
-
тригонометрический многочлен;
«2
»-периодическая
функция.
 -
«2
»-периодическая
функция
-
«2
»-периодическая
функция
Лемма.



 -
ядро
Дирихле.
-
ядро
Дирихле.
Доказательство:
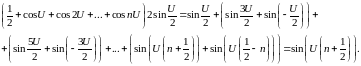
Свойства ядра Дирихле:
1) Бесконечно дифференцируемая функция;
2) Четная;
3)
 -периодическая;
-периодическая;
4)
 .
.
Пусть
 –
-периодическая.
Получим формулу для частной суммы ряда
Фурье:
–
-периодическая.
Получим формулу для частной суммы ряда
Фурье:


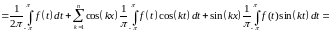
соберём всё в один интеграл

![]()
Выполняя
замену

 ,
получаем формулу
,
получаем формулу


Выполняя
замену в
первом интеграле
 ,
получаем
,
получаем
 .
.
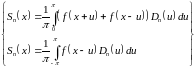 -
Формулы
Дирихле
-
Формулы
Дирихле
3.Сходимость ряда Фурье в точке: Принцип локализации, условие Гёльдера, теорема
Дирихле о поточечной сходимости ряда Фурье.
П.2 Сходимость ряда Фурье в точке
Теорема 1. (Принцип локализации)
Пусть
–
абсолютно интегрируема на
 -
-периодическая.
-
-периодическая.
Тогда

 .
.
 Пусть
Пусть
 .
.

 .
Так как
.
Так как
 и
и
 , следовательно,
, следовательно,
 -
абсолютно интегрируема, следовательно,
-
абсолютно интегрируема, следовательно,
 – абсолютно
интегрируема на
– абсолютно
интегрируема на
 и по лемме Римана
и по лемме Римана
 ∎
∎
Следствие из принципа локализации:
Для

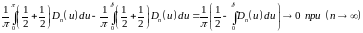 т.е.
т.е.
 .
.
Определение.
Будем говорить, что функция
удовлетворяет в точке
 условию
Гёльдера,
если:
условию
Гёльдера,
если:
 и
и


 -
показатель
Гёльдера.
-
показатель
Гёльдера.
Определим односторонние производные так:

Тогда
если
 , то
, то
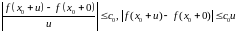 ,
,
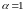 ,
,
т.е. функция, имеющая односторонние производные в данной точке удовлетворяет условию Гёльдера с .
Примеры:
 ,
, ,
,


- удовлетворяет условию Гёльдера.
Теорема 2. (О поточечной сходимости ряда Фурье или Теорема Дирихле)
Пусть
-
абсолютно интегрируема на
,
-
периодична и в точке
удовлетворяет условию Гёльдера. Тогда
ряд Фурье для
в точке
сходится к
 ,
т.е.
,
т.е.
 .
.
Если
непрерывна в точке
 .
.

умножая
на
 и складывая с предыдущим равенством
получаем:
и складывая с предыдущим равенством
получаем:
 Рассмотрим
интеграл, стоящий в скобках, и подставим
выражение для ядра Дирихле:
Рассмотрим
интеграл, стоящий в скобках, и подставим
выражение для ядра Дирихле:

Обозначим
 =
=

 ;
;
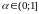
 -
абсолютно интегрируема на
-
абсолютно интегрируема на
 .
.
Тогда
по лемме Римана
 ■
■
