15. Вычисление двойного интеграла

Теорема. Если функция f(x, y) непрерывна в замкнутой области D, ограниченной линиями х = a, x = b, (a < b), y = j(x), y = y(x), где j и y - непрерывные функции и

j £ y, тогда

  Пример. Вычислить интеграл  , если область D ограничена линиями: y = 0, y = x², x = 2.

 y

=

=

  Теорема. Если функция f(x, y) непрерывна в замкнутой области D, ограниченной линиями y = c, y = d (c < d), x = F(y), x = Y(y) (F(y) £ Y(y)), то

 

  Пример. Вычислить интеграл , если область D ограничена линиями y = x, x = 0, y = 1, y = 2.

  y

 

  Пример. Вычислить интеграл  , если область интегрирования D ограничена линиями х = 0, х = у², у = 2.

=

=

  Пример. Вычислить двойной интеграл  , если область интегрирования ограничена линиями ху=1, у =  , х = 2. 

.      

  

 

. 

Выражение двойного интеграла через полярные координаты Одним из частных случаев замены переменных является переход из декартовой в  полярную систему координат (рисунок 1). Рис.1 Рис.2 Якобиан такого преобразования имеет вид Следовательно, дифференциальный элемент в полярных координатах будет равен Пусть область интегрирования R в полярных координатах определяется следующим образом Тогда двойной интеграл в полярных координатах описывается формулой Будем называть полярным прямоугольником область интегрирования, показанную на рисун ке 3 и удовлетворяющую условиям В этом случае формула замены переменных в двойном интеграле имеет вид Будьте внимательны, чтобы не пропустить сомножитель (якобиан) r в правой части этой формулы! Рис.3 Рис.4

Пример 1

Вычислить двойной интеграл  , преобразовав его в полярные координаты. Область интегрирования R представляет собой сектор   круга радиусом  Решение. Область R в полярных координатах описывается множеством  (рисунок 4). Применяя формулу получаем

15. Тройной интеграл. Физический смысл

Тройные интегралы имеют те же свойства, что и двойные интегралы (линейность, аддитивность, формулы среднего значения и т.д.)

I. Вычисление тройных интегралов с помощью повторного интегрирования.

1. Предположим, что функция f(x, y, z) непрерывна в рассматриваемой области T.

Пусть сначала T = [a, b; c, d; e, f] - прямоугольный параллелепипед, проектирующийся на плоскость yz в прямоугольник R = [c, d; e, f]. Тогда

Заменяя в (1) двойной интеграл повторным, получим

Вычисление тройного интеграла сводится к последовательному вычислению трёх определённых интегралов.

Если первые два интеграла в (2) объединить в двойной, то будем иметь

где P = [a, b; c, d] - проекция параллелепипеда T на плоскость xy.

Заметим, что в этих случаях можно менять роли переменных.

Пусть область T заключена между плоскостями x = a и x = b, причём каждое сечение области T плоскостью  представляет собой квадрируемую фигуру G(x)(рис. 1). Тогда

Пусть теперь тело T представляет собой "цилиндрический брус", ограниченный снизу и сверху, соответственно, поверхностями z = z₁(x, y) и z = z₂(x, y), проектирующиеся на плоскость xy в некоторую квадрируемую фигуру G (рис.2), z₁(x, y) и z₂(x, y) - непрерывны в G. Тогда

Если G = {(x, y): a  x  b, y1(x)  y  y2(x)}, то

Отметим, что наряду с указанными формулами имеют место и им подобные, получающиеся перестановкой переменных x, y и z.

II. Замена переменных в тройном интеграле  состоит в переходе от переменных x, y, z к новым переменным u, v, w по формулам

Если выполняются условия

Отображение (6) взаимно однозначно;

Функции в (6) непрерывно - дифференцируемы в области 

Якобиан отображения

то имеет место формула

Формулы (6) называют криволинейными координатами (u, v, w) в области T. Рассмотрим примеры криволинейных координат.

1. Цилиндрические координаты представляют соединение полярных координат в плоскости xy с обычной декартовой аппликатой z (рис. 3).

Пусть M(x, y, z) - произвольная точка в пространстве xyz, P - проекция точки M на плоскость xy. Точка M однозначно определяется тройкой чисел  - полярные координаты точки P, z - аппликата точки M. Формулы, связывающие их с декартовыми, имеют вид

Якобиан отображения (8) 

2. Сферические координаты. Пусть M(x, y) - произвольная точка в пространстве xyz, P - проекция точки M на плоскость xy. Точка M однозначно задаётся тройкой чисел  , где r - расстояние точки M до точки 0,  - угол между лучами OM и OZ,  - полярный угол точки P на плоскости xy. Тройка чисел  называется сферическими координатами точки M.

Они связаны с прямоугольными формулами

Якобиан отображения  . Иногда используются обобщённые сферические координаты.

Объём V кубируемой области T (кубического тела) в пространстве xyz выражается формулой

Переходя в этом равенстве к новым переменным по формулам (6), получим выражение объёма области T в криволинейных координатах

Пусть T - материальное тело (кубируемая область) с плотностью 

Тогда

- масса тела.

Пример1. Вычислить объём тела, ограниченного поверхностями: x² + y² + z² = a², x² + y² - ax = 0. (рис. 5)

Решение. Рассмотрим одну четвёртую часть тела, лежащёю в первом октанте. Часть поверхности  вырезанная цилиндром, проектируется в область  . Тогда

Перейдём в интеграле к цилиндрическим координатам по формулам (8). При этом уравнение окружности x? + y? - ax = 0 преобразуется в кривую  а уравнение поверхности  - к виду 

Таким образом

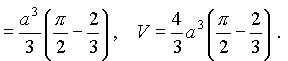
Пример 2. Вычислить интеграл

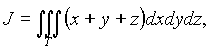
где T - область, ограниченная поверхностями 

Решение. Перейдём в интеграле к сферическим координатам по формулам (9). Тогда область интегрирования можно задать неравенствами

А, значит,

15. Вычисление тройного интеграла

Процедура вычисления тройного интеграла аналогична соответствующей операции для двойного интеграла. Для ее описания введем понятие правильной трехмерной области:

Определение 9.1. Трехмерная область V, ограниченная замкнутой поверхностью S, называется правильной, если:

1. любая прямая, параллельная оси Оz и проведенная через внутреннюю точку области, пересекает S в двух точках;

2. вся область V проектируется на плоскость Оху в правильную двумерную область D;

3. любая часть области V, отсеченная от нее плоскостью, параллельной какой-либо из координатных плоскостей, обладает свойствами 1) и 2).

Рассмотрим правильную область V, ограниченную снизу и сверху поверхностями  z=χ(x,y)  и  z=ψ(x,y) и проектирующуюся на плоскость Оху в правильную область D, внутри которой х изменяется в пределах от а до b, ограниченную кривыми y=φ1(x) и    y=φ2(x) (рис.1). Зададим в области V непрерывную функцию f(x, y, z). 

Определение 9.2. Назовем трехкратным интегралом от функции f(x, y, z) по области V выражение вида:

. (9.1) 

Трехкратный интеграл обладает теми же свойствами, что и двукратный. Перечислим их без доказательства, так как они доказываются аналогично случаю двукратного интеграла.

1. Если область V разбить на две области V1 и V2 плоскостью, параллельной какой-либо из координатных плоскостей, то трехкратный интеграл по области V равен сумме трехкратных интегралов по областям V1 и V2.

2. Если т и М – соответственно наименьшее и наибольшее значения функции f(x,y,z) в области V, то верно неравенство. mV ≤ IV ≤ MV, где V – объем данной области, а IV – трехкратный интеграл от функции f(x,y,z) по области V.

3. Трехкратный интеграл IV от непрерывной функции f(x,y,z) по области V равен произведению его объема V на значение функции в некоторой точке Р области V:  (9.2)

Вычисление тройного интеграла.

Теорема 9.1. Тройной интеграл от функции f(x,y,z) по правильной области V равен трехкратному интегралу по той же области:

. (9.3)

Доказательство.

Разобьем область V плоскостями, параллельными координатным плоскостям, на п правильных областей  . Тогда из свойства 1 следует, что

где   - трехкратный интеграл от функции f(x,y,z) по области  .

Используя формулу (9.2), предыдущее равенство можно переписать в виде: .

Из условия непрерывности функции f(x,y,z) следует, что предел интегральной суммы, стоящей в правой части этого равенства, существует и равен тройному интегралу  . Тогда, переходя к пределу при  , получим:

IV =  ,

что и требовалось доказать.

Замечание.

Аналогично случаю двойного интеграла можно доказать, что изменение порядка интегрирования не меняет значения трехкратного интеграла.

Пример. Вычислим интеграл   где V – треугольная пирамида с вершинами в точках (0, 0, 0), (1, 0, 0), (0, 1, 0) и (0, 0, 1). Ее проекцией на плоскость Оху является треугольник с вершинами (0, 0), (1, 0) и (0, 1). Снизу область ограничена плоскостью z = 0, а сверху – плоскостью x + y + z = 1. Перейдем к трехкратному интегралу:

 Множители, не зависящие от переменной интегриро-вания, можно вынести за знак соответствующего интеграла: