1.3.3. Условие Лежандра
Для того чтобы функционал (1.7) в задаче с закреплёнными границами достигал на кривой y(x) минимума или максимума, необходимо, чтобы, помимо уравнения Эйлера, вдоль этой кривой выполнялось условие:
или
. (1.16)
Условие (1.16) называется условием Лежандра.
В точках где
,
возможны
изломы. Наконец, если
равно нулю тождественно, то функционал
является вырожденным [10].
В вариационном исчислении, как правило, имеют дело только с первой производной. Это объясняется тем, что в реальных условиях обычно ясно с каким экстремумом мы имеем дело. Поэтому в большинстве случаев пользуются только первой вариацией.
1.3.4. Обсуждение уравнения Эйлера
Для простейшего функционала Эйлера (1.3):
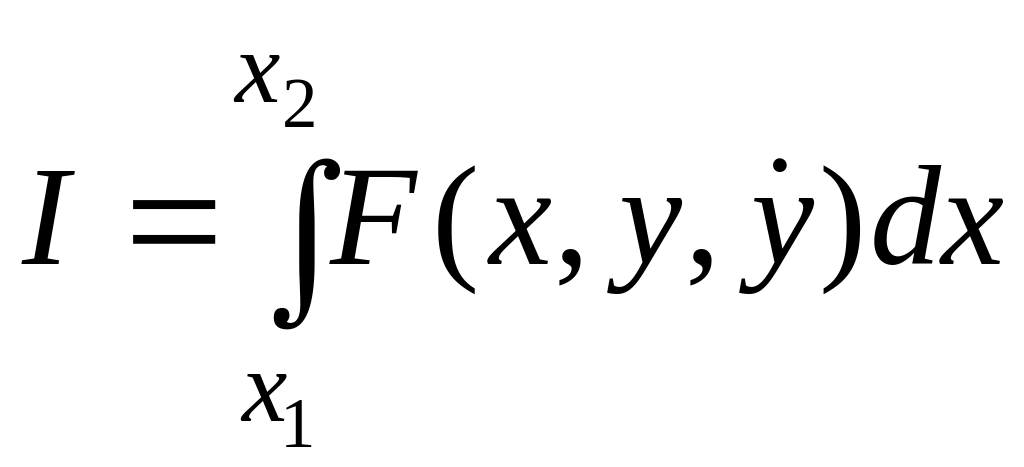
уравнение Эйлера имеет вид (1.14):
Произведём полное дифференцирование по x второго члена уравнения:
(1.17)
При
проведении полного дифференцирования
(1.17) необходимо учесть, что
есть функция трёх аргументов: x,
y
и
,
и что y
и
в
свою очередь являются функциями от x
[1,10].
И тогда уравнение Эйлера можно записать в виде:
(1.18)
Таки образом, в общем случае уравнение Эйлера является нелинейным дифференциальным уравнением второго порядка. Решения уравнения (1.18) для общего случая не существует. Поэтому рассмотрим некоторые частные случаи, когда решение упрощается.
1.
Пусть подынтегральная функция F
не зависит от y,
тогда уравнение Эйлера имеет вид
,
и, следовательно:
(1.19)
Из (1.19) определяют как функцию от x и поэтому искомая функция y(x) может быть выражена в виде интеграла.
2.
Подынтегральная функция F
не зависит явно от x,
тогда
.
В этом случае уравнение Эйлера (1.18)
примет вид:
(1.20)
Умножим
(1.20) на
,
при условии, что
:
, (1.21)
Выражение (1.21) можно записать в виде:
,
из которого следует, что искомая функция должна удовлетворять уравнению:
(1.22)
Уравнение (1.22) не содержит в явном виде х, поэтому его всегда можно проинтегрировать.
Уравнение (1.22) принято называть первым интегралом уравнения Эйлера.
3. Функция F зависит только от . В этом случае уравнение Эйлера имеет вид:
,
из
которого следует
,
тогда
,
т.е.
;
и, следовательно,
Таким образом, если функционал зависит только от производной искомой функции, то экстремалями всегда будут прямые линии.
4.
Пусть значение
тождественно равно нулю:
. (1.23)
Выражение
(1.23) выполняется в том случае, когда,
либо
,
либо
.
Это означает, что функционал или вовсе не зависит от производной искомой функции, или зависит от неё линейно. Такие функционалы называются вырожденными. Они обладают особыми свойствами [10].
1.3.5. Примеры на безусловный экстремум с закреплёнными границами. Применение уравнения Эйлера
Пример 1.1. Среди всех кривых, соединяющих на плоскости две фиксированные точки А(x0,y0) и В(x1,y1) определить кривую имеющую минимальную длину.
Представим эту задачу геометрически. На плоскости x0y заданы две точки А(x0,y0) и В(x1,y1).
Выберем на кривой y(x) элементарный участок dℓ и образуем прямоугольный треугольник с гипотенузой dℓ и катетами dx и dy. Тогда
dℓ2= dx2 + dy2.
Проведя, соответствующие преобразования получаем:
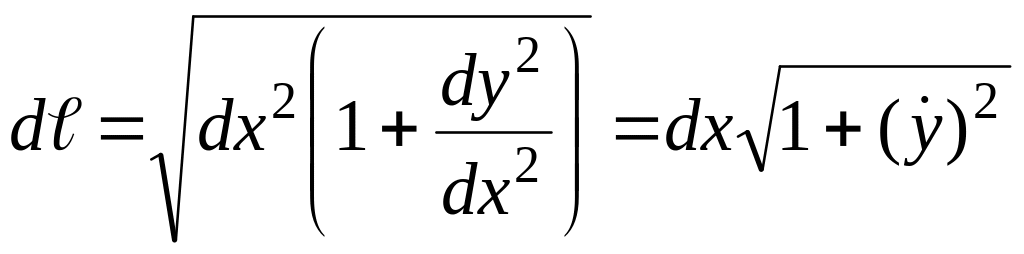, (1.24)
Тогда
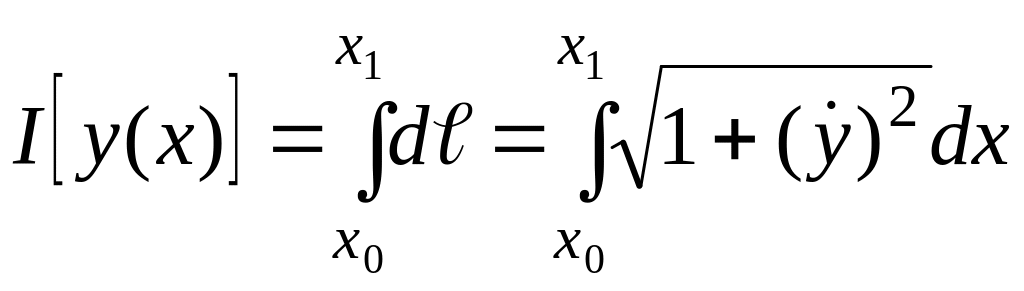(1.25)
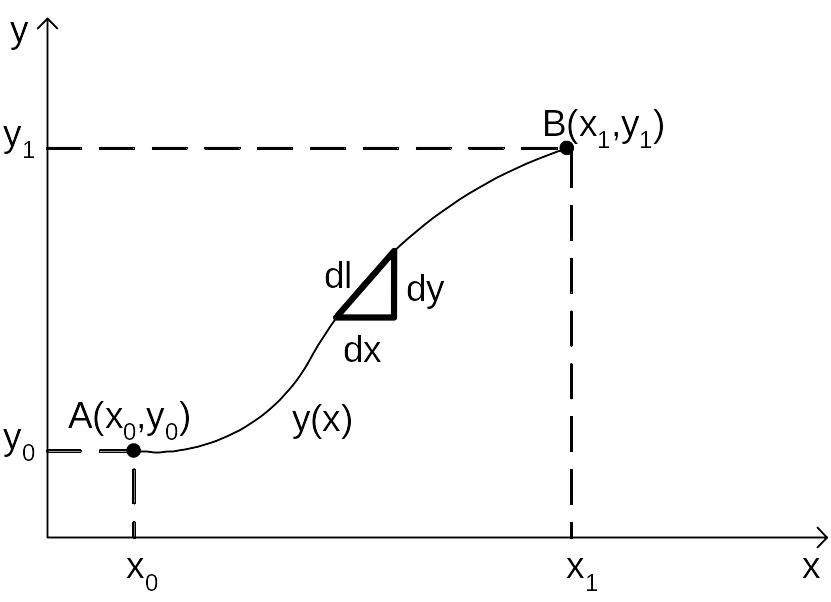
Рис. 1.3 Кривая минимальной длины.
подынтегральная функция функционала (1.25) имеет вид:
. (1.26)
Запишем
уравнение Эйлера:
.
Продифференцируем
уравнение Эйлера:
,
т.к. в подынтегральной
функции F(y)
отсутствует явно координата y.
Отсюда следует, что производная функции
F
по
будет равна постоянной величине:
. (1.27)
Далее продифференцируем (1.26):
, (1.28)
Приравняем правые части (1.27) и (1.28):
,
и после соответствующих преобразований получаем окончательно уравнение прямой линии:
.
Таким образом, искомой экстремалью y(x) является прямая линия, соединяющая на плоскости две фиксированные точки А и В.
Постоянные интегрирования со и с1 находятся из условий:
.
Пример 1.2. Задача о брахистохроне. Напомним постановку задачи, которая была поставлена в 1669 г. И. Бернулли и кратко изложена в начале знакомства с классическим вариационным исчислением (рис 1.1).
Среди всех гладких кривых, проходящих через две фиксированные точки А(а, α) и В(в, β) найти кривую, по которой тяжёлая материальная точка переместится под действием силы тяжести из точки А в точку В за кратчайшее время при условии, что начальная скорость точки равна нулю и α >β [7].
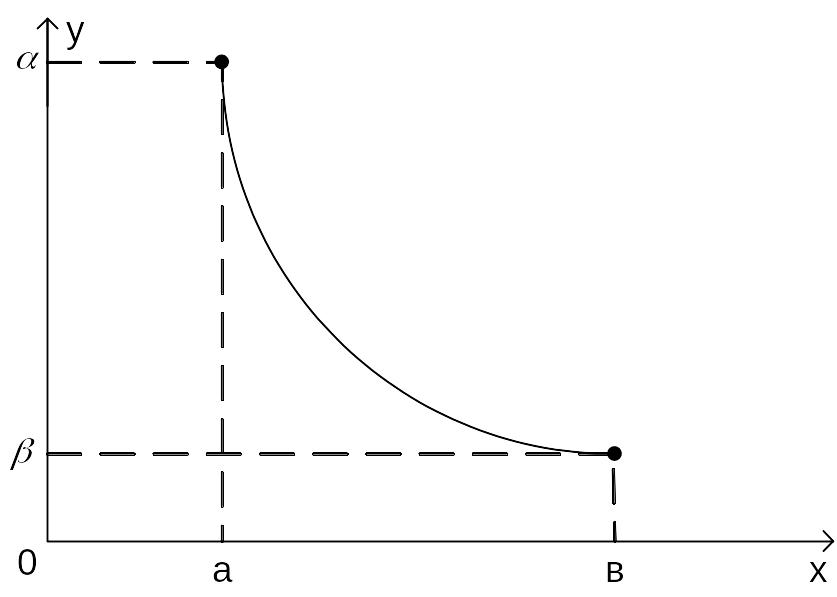
Рис. 1.4 Кривая кратчайшего времени.
Эта задача связана с минимизацией времени движения. Поэтому функционал можно представить в виде:
(1.29)
Т.е. функционалом является время движения:
Для
того чтобы связать время t
с функцией y(x)
и её производной
воспользуемся
законом сохранения энергии. Согласно
этому закону на всём пути движения точки
полная энергия Е
остаётся постоянной и равняется сумме
кинетической и потенциальной энергий:
, (1.30)
где: m – масса тяжёлой материальной точки; V – скорость движения точки; g – ускорение свободного падения точки; y(x) – искомая функция перемещения точки в зависимости от x.
Скорость, с учетом (1.24), можно представить в следующем виде:
, (1.31)
и согласно (1.37):
. (1.32)
Приравняем правые части выражений (1.31) и (1.32):
.
Отсюда:
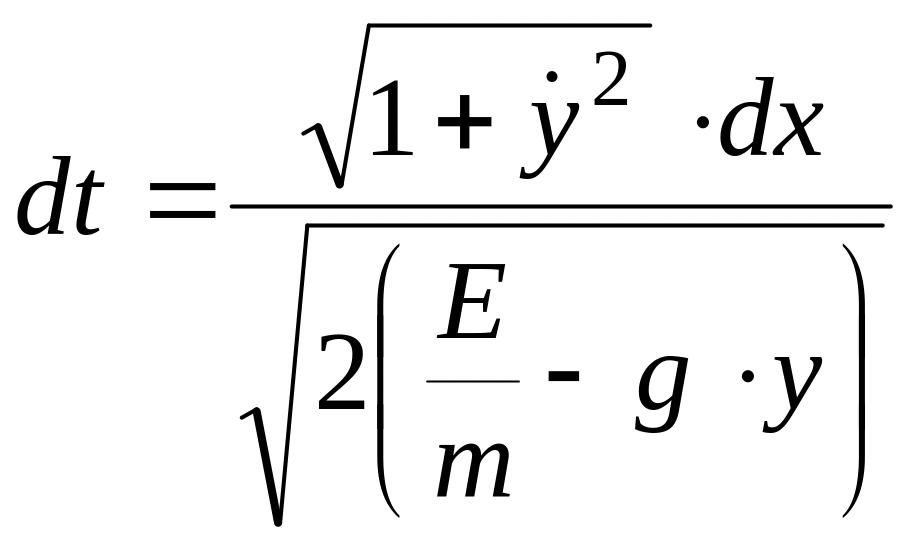. (1.33)
Подставим (1.33) в (1.29):
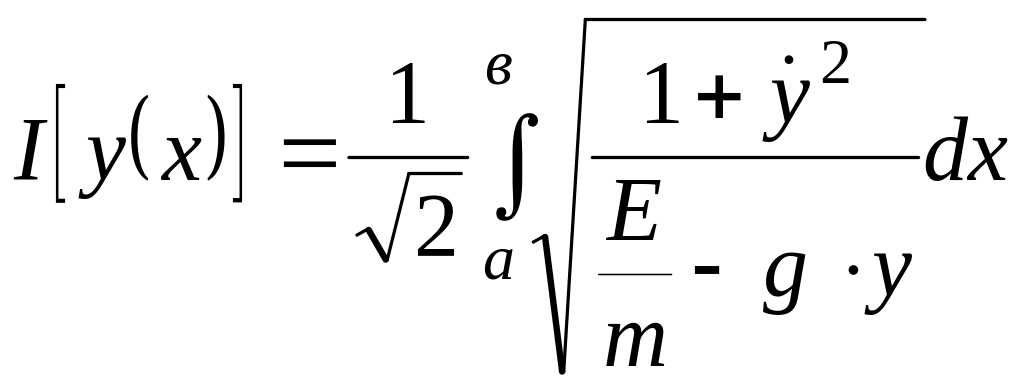
Определим постоянную Е, по условию V=0 при x=а. С учетом того, что E=mgα, тогда окончательно получаем:
(1.34)
Подынтегральная функция функционала (1.34) имеет вид:
,
которая не зависит явно от х. Поэтому уравнение Эйлера, согласно (1.22), принимает вид:
. (1.35)
Это уравнение называют первым интегралом Эйлера.
В результате дифференцирования выражения (1.35) получаем:
. (1.36)
Для
решения уравнения (1.36) вводят параметр
,
тогда:
(1.37)
Уравнения (1.37) задают семейство циклоид, которое зависит от параметров с1 и с2. Эти параметры можно определить из условия прохождения циклоид через точки А и В.
Для подтверждения того, что найденная экстремаль (1.37) соответствует минимуму, проведём проверку с помощью теории Лежандра.
Пусть
Для
имеем:
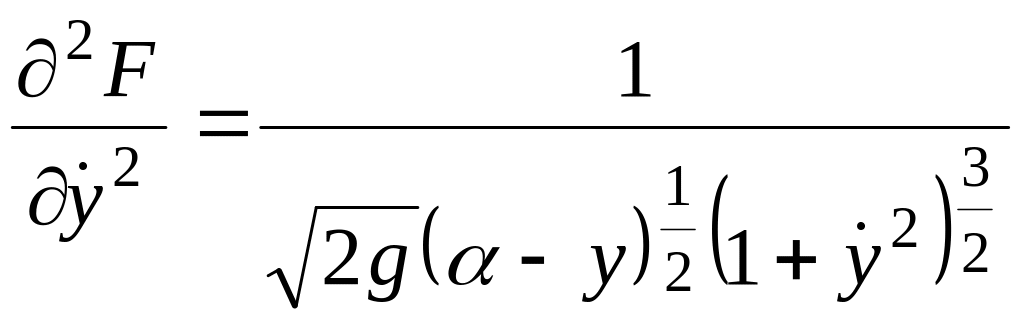
Подучили подтверждение, что функционал (1.34) на кривой y(x) (1.37) достигает минимума, и материальная точка на кривой y(x) переместится из точки А в точку В за минимальное время.
Пример 1.3. Найти экстремали функционала:
(1.38)
при условии, что y(1)= 4, y(4)= 1.
Подынтегральная
функция
не зависит от y.
Это первый частный случай, когда решение
уравнения Эйлера упрощается.
,
значит
(1.39)
Интегрируя выражение (1.39), получаем:
(1.40)
Экстремали (1.40) являются гиперболами. Постоянные интегрирования определяются из условий (1.38):
.
Отсюда с =-8,
с1 =0.
Окончательно получаем гиперболу: y=4/x (рис. 1.5.).
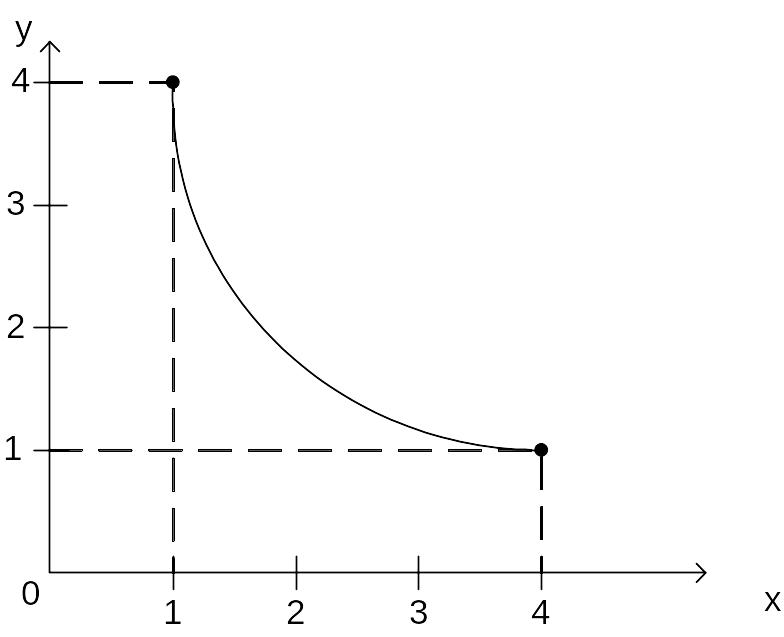
Рис. 1.5. Экстремаль функционала (1.38) гипербола.
А значения функционала с учётом экстремали (1.40) будет равно
.