Эмпирическая функция распределения

Пусть п_х – число наблюдений, при которых наблюдалось значение признака Х, меньшее х. При объеме выборки, равном п, относительная частота события Х < х равна п_х / п.

Определение 1. Функция, определяющая для каждого значения х относительную частоту события Х < х,

F* (х) = п_х / п (3)

называется эмпирической функцией распределения, или функцией распределения выборки.

В отличие от эмпирической функции распределения F*(х) выборки функция распределения F(x) генеральной совокупности называется теоретической функцией распределения. Различие между ними состоит в том, что функция F(x) определяет вероятность события Х < х, a F*(х) — относительную частоту этого события. Из теоретических результатов обшей теории вероятностей (закон больших чисел) следует, что при больших п вероятность отличия этих функций друг от друга близка к единице:

(4)

Нетрудно увидеть, что F*(х) обладает всеми свойствами F(х), что вытекает из ее определения (3):

1. значения F* (х) принадлежат отрезку [0, 1]

2. F* (х) является неубывающей функцией

3. пусть х_т и х_М — соответственно, минимальная и максимальная варианты, тогда F* (х) = 0 при х ≤ х_т и F* (х) = 1 при х ≥ х_М.

Сама же функция F*(х) служит для оценки теоретической функции распределения F (x) генеральной совокупности.

Пример 3. Построить эмпирическую функцию по заданному распределению выборки:

хi	2	4	6
пi	10	15	25

Решение. Находим объем выборки: п = 10 + 15 + 25 = 50. Наименьшая варианта равна 2, поэтому F* (х) = 0 при х ≤ 2. Значение Х < 4 (при х₁ = 2) наблюдалось 10 раз, значит, F* (х) = 10/50 = 0,2 при 2 < х < 4. Значения Х < 6 (а именно, х₁ = 2 и х₂ = 4) наблюдались 10 + 15 = 25 раз, значит, при 4 < х < 6 функция F* (х) = 25/50 = 0,5. Поскольку х = 6 – максимальная варианта, то F* (х) = 1 при х > 6. Напишем формулу искомой эмпирической функции:

График этой функции показан на рис. 1.

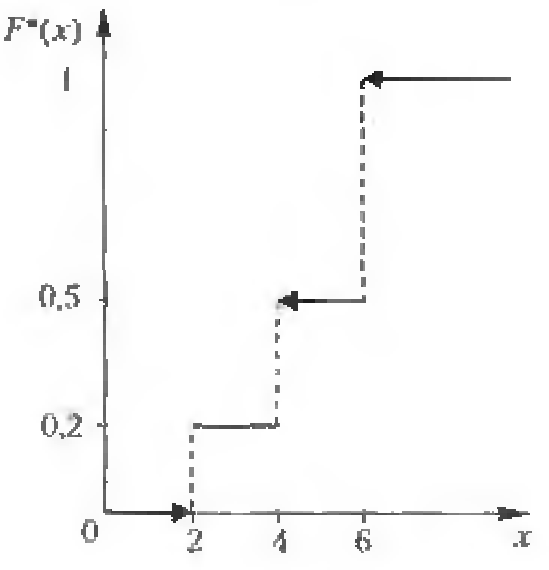
Рис. 1 График эмпирической функции по данным примера 3

Полигон и гистограмма

Каждую пару значений (х_i, п_i) из распределения выборки можно трактовать как точку на координатной плоскости. Точно так же можно рассматривать и пары значении (х_i, w_i) относительного распределения выборки.

Ломаная, отрезки которой соединяют точки (х_i, п_i), называется полигоном частот

Ломаная, соединяющая на координатной плоскости точки (х_i, w_i), называется полигоном относительных частот.

На рис. 2 показан полигон относительных частот для распределения, приведенного в примере 2.

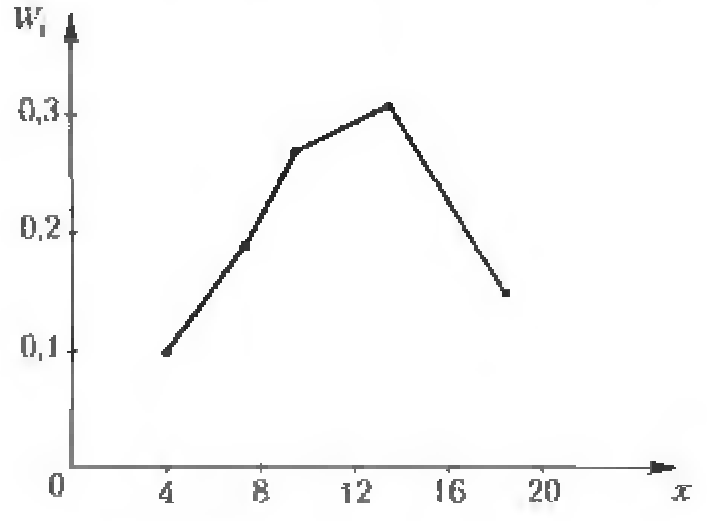
Рис. 2. Полигон относительных частот распределении по данным примера 2

Для случая непрерывного признака Х удобно разбить интервал (х_min, х_max) его наблюдаемых значении на несколько частичных интервалов данной h каждый и найти для каждого из этих интервалов сумму частот n_j, попавших в него.

Ступенчатая фигура, состоящая из прямоугольников с основаниями длиной h и высотами n_j / h (плотность частоты), называется гистограммой частот.

Геометрический смысл гистограммы: нетрудно увидеть, что площадь ее равна сумме всех частот, или объему выборки. На рис. 3 изображена гистограмма выборки объема n = 100.

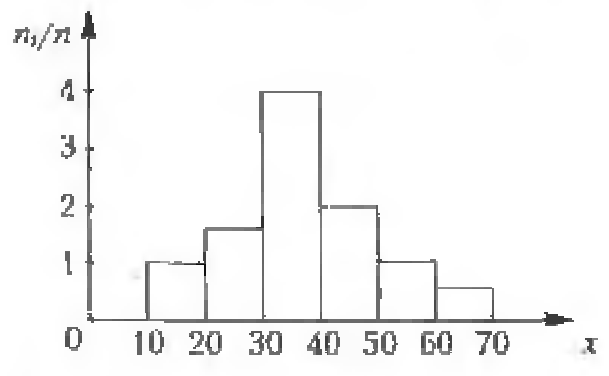
Рис. 3. Пример гистограммы выборки объема n = 100

Аналогичным образом определяется и гистограмма относительных частот. Высоты прямоугольников, составляющих ступенчатую фигуру, определяются отношениями сумм относительных частот, попадающих в интервал (x_min + (j – 1) h, x_min + j h), к длине интервала h, т.е. величинами w_j / h. В этом случае площадь гистограммы относительных частот равна единице (сумме относительных частот выборки).