
- •Приближенные числа
- •Правила вычислений с приближенными числами.
- •Приближенное решение алгебраических и трансцендентных уравнений. Отделение корней и уточнение приближенных корней. Графическое решение уравнений.
- •Метод половинного деления (метод «вилки»).
- •Метод хорд.
- •Метод Ньютона (метод касательных).
- •Метод итерации. Приведение уравнений к виду, удобному для итерации.
- •Приближенное решение систем линейных уравнений. Метод итераций.
- •Приближенное решение систем нелинейных уравнений. Метод итерации.
- •Постановка задачи интерполирования функций. Общее решение задачи интерполирования функции полиномом.
- •Интерполяционная формула Лагранжа
- •Интерполирование сплайнами
- •14 Аппроксимирование функций (15 не нашли)
- •Аппроксимирование функций. Метод ортогональных функций.
- •Квадратурная формула Ньютона-Котеса
- •Квадратурная формула Гаусса
- •Численные метода решения задачи Коши для обыкновенных дифференциальных уравнений. Метод Эйлера. Метод Эйлера-Коши
- •Метод Рунге-Кутта
- •Редукция к задаче Коши двухточечной краевой задачи для линейного уравнения второго порядка.
- •Метод коллокации.
- •23.Аппроксимация производных конечно-разностными соотношениями.
- •Метод конечных разностей численного решения обыкновенных дифференциальных уравнений.
- •Принципы построения сеток на плоскости и в пространстве.
- •26. Построение разностных схем для уравнений параболического типа.
- •27. Экстремумы функций. Классификация методов безусловной оптимизации.
- •28. Общая характеристика методов оптимизации нулевого порядка.
- •Метод прямого поиска (метод Хука-Дживса).
- •Метод деформируемого многогранника (метод Нелдера-Мида).
- •Метод вращающихся координат (метод Розенброка).
- •Метод параллельных касательных (метод Пауэлла).
- •Общая характеристика методов оптимизации первого порядка.
- •34.Метод наискорейшего спуска
- •35. Общая характеристика методов оптимизации второго порядка. Метод Ньютона.
- •36. Метод Ньютона с регулировкой шага (метод с переменной метрикой)
- •37. Метод статистических испытаний (метод Монте-Карло)
- •38. Вычисление кратных интегралов методом Монте-Карло
- •39. Структура искусственной нейронной сети (инс)
- •40. Компьютерная модель нейрона (нейроэлемента, нэ)
- •41. Функции активации нейроэлементов
- •45.Методы обучения элементарного перцептрона.
- •46.Многослойный перцептрон.
- •47. Понятие обучающей выборки.
Приближенное решение алгебраических и трансцендентных уравнений. Отделение корней и уточнение приближенных корней. Графическое решение уравнений.
Пусть дано уравнение
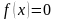 , (1)
, (1)
где f(x) – заданная функция действительного или комплексного аргумента x.
Всякое значение с,
обращающее функцию f(x)
в нуль, т.е. для которого выполняется
равенство
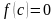 ,
называется корнем
уравнения (1) или корнем
(нулем)
функции f(x).
,
называется корнем
уравнения (1) или корнем
(нулем)
функции f(x).
Приближенное нахождение корней уравнения складывается из двух этапов:
1) отделение корней, т. е. нахождение наиболее узких интервалов [a, b], в каждом из которых содержится один и только один корень данного уравнения (количество интервалов определяется видом функцииf(x));
2) уточнение приближенных корней, т. е. вычисление корней с заданной степенью точности.
Для отделения корней чаще
всего применяют графический
метод, основанный на
том, что вещественные корни уравнения
(1) являются точками пересечения графика
функции f(x)
с осью x.
Следовательно, построив график
 ,
можно принять за приближенные значения
корней абсциссы точек пересечения
графика с осью x.
,
можно принять за приближенные значения
корней абсциссы точек пересечения
графика с осью x.
Иногда, при применении
графического метода, удобно функцию
f(x)
представить в виде
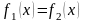 и затем, построив графики
и затем, построив графики
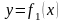 и
и
 ,
найти абсциссы их точек пересечения,
которые и будут приближенными значениями
корней.
,
найти абсциссы их точек пересечения,
которые и будут приближенными значениями
корней.
Пример.
Отделить
корни уравнения
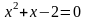 .
.
Можно
построить график функции
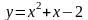 .
Точки пересечения этого графика с осью
x
будут являться приближенными корнями
уравнения.
.
Точки пересечения этого графика с осью
x
будут являться приближенными корнями
уравнения.
Кроме
того, можно исходное уравнение записать
в виде
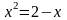 и построить графики
и построить графики
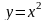 и
и
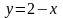 .
Абсциссы точек пересечения этих графиков
можно принять за приближенные корни
заданного уравнения.
.
Абсциссы точек пересечения этих графиков
можно принять за приближенные корни
заданного уравнения.
Еще одним способом отделения корней является исследование функции f(x) с целью установления интервалов, на которых происходит изменение знака функции.
При этом полезна следующая
теорема: Пусть функция
f(x)
непрерывна на интервале [a,
b]
и принимает на концах данного интервала
значения разных знаков,
т. е.
 <0.
Тогда внутри интервала [a,
b]
найдется такая точка с,
значение функции в которой равно нулю,
т.е.
и которая является корнем данного
уравнения.
<0.
Тогда внутри интервала [a,
b]
найдется такая точка с,
значение функции в которой равно нулю,
т.е.
и которая является корнем данного
уравнения.
Корень
с
заведомо будет единственным на [a,
b],
если производная
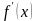 существует и сохраняет постоянный знак
внутри данного интервала, т.е. если
>0
или
<0.
существует и сохраняет постоянный знак
внутри данного интервала, т.е. если
>0
или
<0.
Численные методы, используемые для уточнения приближенных корней, применяются для каждого найденного интервала заданного уравнения.
Метод половинного деления (метод «вилки»).
Пусть дано уравнение .
Определяем, какие корни требуется найти, например, только положительные или только отрицательные и т. д. Затем графическим методом находим интервалы, в каждом из которых находится только один корень данного уравнения.
Пусть искомый корень с
принадлежит интервалу [a,
b]. Функция
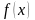 непрерывна на [a, b]
и выполняется условие
<0.
Разделим отрезок [a,
b] пополам точкой
непрерывна на [a, b]
и выполняется условие
<0.
Разделим отрезок [a,
b] пополам точкой
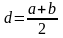 и получим уже два интервала: [a,
d] и [d,
b]. Далее выбираем тот
отрезок, на концах которого функция
f(x)
принимает значения разных знаков (это
значит, что внутри данного отрезка
содержится корень уравнения) и опять
делим его пополам. Повторяем все эти
действия до тех пор, пока длина отрезка,
содержащего корень, не станет меньше
погрешности, с которой ищется корень.
и получим уже два интервала: [a,
d] и [d,
b]. Далее выбираем тот
отрезок, на концах которого функция
f(x)
принимает значения разных знаков (это
значит, что внутри данного отрезка
содержится корень уравнения) и опять
делим его пополам. Повторяем все эти
действия до тех пор, пока длина отрезка,
содержащего корень, не станет меньше
погрешности, с которой ищется корень.
Пример.
Методом половинного деления
найти корень уравнения
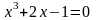 .
.
Графически находим интервал [0,4; 0,5], в котором находится действительный корень данного уравнения.f(0,4) = -0,136 < 0;
f(0,5) = 0,125 > 0;
Условие нахождения корня в рассматриваемом интервале выполняется, т. е.
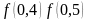 <
0.
<
0.
Интервал [0,4; 0,5] делим пополам
точкой
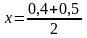 = 0,45.
= 0,45.
Проверим условие < 0.
f(0,4) = -0,136 < 0; f(0,5) = 0,125 > 0; f(0,45) = -0,00888 < 0.
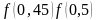 <
0, следовательно, выбираем [0,45; 0,5]. Этот
интервал делим пополам:
<
0, следовательно, выбираем [0,45; 0,5]. Этот
интервал делим пополам: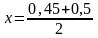 = 0,475.
= 0,475.
Методом половинного деления найти корень уравнения .
Графически находим интервал [0,4; 0,5] для корня
f(0,4) = -0,136 < 0; f(0,5) = 0,125 > 0;
Условие нахождения корня в рассматриваемом интервале выполняется, т. е.
< 0.
Интервал [0,4; 0,5] делим пополам точкой = 0,45.
Проверим условие < 0.f(0,4) = -0,136 < 0;
f(0,5) = 0,125 > 0;
f(0,45) = -0,00888 < 0.
< 0, следовательно, выбираем [0,45; 0,5].
В итоге найдем, что при
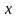 = 0,453398 f(0,453398) =
0,0000009, т.е. корень.
= 0,453398 f(0,453398) =
0,0000009, т.е. корень.
