9. Положительно-определенные квадратичные формы. Критерий Сильвестра.

• Квадратичная форма 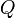  называется положительно (отрицательно) определённой, если для любого 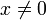  выполнено неравенство 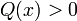 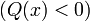  . Положительно определённые и отрицательно определённые формы называются знакоопределёнными.

• Квадратичная форма 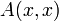  называется знакопеременной, если она принимает как положительные, так и отрицательные значения.

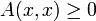
• Квадратичная форма   называется положительно (отрицательно) полуопределенной, если     для любого  .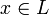

Квадратичные формы

Также можно сформулировать положительную определённость через квадратичные формы. Пусть   будет полем вещественных ( ) или комплексных ( ) чисел, а   будет векторным пространством над  . Эрмитова форма

является билинейным отображением, притом числом, сопряженным  , будет  . Такая функция   называется положительно определённой, когда   для любого ненулевого  . Для любой квадратичной формы существует базис, в котором её матрица диагональна, а сама форма имеет канонический вид:

Критерий Сильвестра

Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой.

Пусть квадратичная форма имеет в каком-то базисе матрицу

Тогда эта форма положительно определена, если и только если все её главные (угловые) миноры   положительны. Форма отрицательно определена, если и только если знаки   чередуются, причём  . Здесьглавными минорами матрицы   называются определители вида

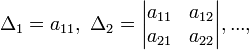
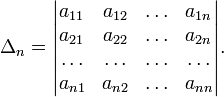
Для неотрицательно определённых матриц критерий действует только в одну сторону: если форма неотрицательно определена, то главные миноры неотрицательны. Обратное неверно. Например, матрица

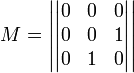
не является неотрицательно определённой — так как, например,   для  . В то же время все её главные миноры равны 0, то есть неотрицательны.

Доказательство

Критерий положительной определённости квадратичной формы

Доказательство критерия Сильвестра основано на методе Якоби приведения квадратичной формы к каноническому виду.

Для положительной определённости квадратичной формы необходимо и достаточно, чтобы главные миноры её матрицы были положительны.

1. «Необходимо.» Имеется положительно определённая квадратичная форма. j-ый диагональный элемент положителен, так как k(x)>0 в том числе и для вектора со всеми нулевыми координатами, кроме j-ой. При приведении матрицы к каноническому виду не будет нужно переставлять строки, и знаки главных миноров матрицы не изменятся. А в каноническом виде диагональные элементы положительны, и миноры положительны; следовательно, (так как их знак не менялся при преобразованиях), у положительно определённой квадратичной формы в любом базисе главные миноры матрицы положительны.

2. «Достаточно.» Имеется положительность миноров. Первый минор определяет знак первого диагонального элемента в каноническом виде. Знак отношения M_i+1/M_i определяет знак i+1-ого элемента в диагональном виде. Так получим, что в каноническом виде все элементы на диагонали положительные, то есть квадратичная форма определена положительно.^[1]

[править]Критерий отрицательной определённости квадратичной формы

Для отрицательной определённости квадратичной формы необходимо и достаточно, чтобы главные миноры чётного порядка её матрицы были положительны, а нечётного порядка — отрицательны.

Доказательство сводится к предыдущему случаю, так как матрица   является отрицательно определённой тогда и только тогда, когда матрица   является положительно определённой. При замене матрицы   на противоположную главные миноры нечётного порядка меняют знак, а главные миноры чётного порядка остаются такими же.