9. Квадратичные формы и их применение

Определение. Квадратичной формой   переменных  ,принимающих числовые значения , называется числовая функция вида

   ,

где  - числа, называемые коэффициентами квадратичной формы.

Определение. Матрицей квадратичной формы   переменных  , называется симметрическая матрица порядка  , элементы главной диагонали которой совпадают с коэффициентами при квадратах переменных, а каждый недиагональный элемент, расположенный в  ой строке  ом столбце, равен половине коэфициента при   в квадратичной форме.

Определение. Рангом квадратичной формы называется ранг её матри-цы. Квадратичная форма может быть записана в матричном виде   где  матрица квадратичной формы и  .

Определение. Квадратичная форма называется канонической (имеет канонический вид), если коэфициенты  при  , то есть, если матрица квадратичной формы диагональная и следовательно

.,

где не все коэффициенты   равны нулю.

Теорема (Лагранжа). Для всякой квадратичной формы существует такой базис, в котором квадратичная форма имеет канонический вид.

Определение. Нормальным видом квадратичной формы называется такой канонический вид, в котором коэффициенты при квадратах неизвестных (не считая нулевых) равны  .

Определение. Квадратичная форма   называется положительно

(отрицательно) определённой, если   при всех

 и положительно (отрицательно) полуопределённой,если   при всех  .

Теорема (критерий Сильвестра). Для того чтобы квадратичная форма   была положительно определённой, необходимо и достаточно чтобы все угловые миноры матрицы квадратичной формы были положительны,то есть, чтобы

Здесь  -угловые миноры матрицы квадратичной формы.

Следствие. Для того чтобы квадратичная форма   была отрицательно определённой, необходимо и достаточно, чтобы знаки угловых миноров матрицы квадратичной формы чередовались следующим образом: 

Примеры

1. Привести квадратичную форму к каноническому виду методом Лагранжа и записать соответствующее преобразование

  . 

Решение. Следуя алгоритму метода Лагранжа, выделим вначале в квад-ратичной форме все члены, содержащие  , и дополним их до полного квадрата: 

   .

Сделаем в этом выражении замену   и подставим его в квадратичную форму. Получим:

  . 

Далее выделим в   члены, содержащие   и проделаем с ними анало-гичную процедуру: 

    

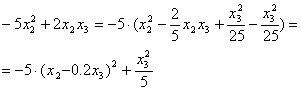
Если положить  , то квадратичная форма уже не будет содержать смешанных произведений. Примем также  , тогда

канонический вид квадратичной формы есть 

  .

Соответствующее преобразование от переменных   к переменным   имеет вид:

  .

2. Найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду, и записать соответствующий канонический вид этой формы:

  . 

Решение. В исходном базисе   матрица оператора, соответствующая данной квадратичной форме, есть

  .

Эта матрица будет определять квадратичную форму  канонического вида в ортонормированном базисе  , составленном из собственных векторов матрицы  . Найдем их.

Характеристическое уравнение для матрицы   имеет вид

  .

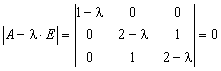Откуда следует

   и  .

Как известно собственные векторы матрицы находятся из уравнений

  .

Для случая   имеем:

  . 

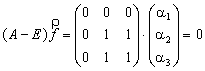Ранг матрицы этой системы уравнений (относительно  ) равен 1. Следовательно, ФСР системы состоит из двух линейно независимых решений.

 Как видно из данной системы, величина   принимает произвольные значения, а величины   связаны соотношением  . В качестве собственных можно выбрать, например, векторы

 

  Эти векторы ортогональны:   (если бы они оказались не ортогональными, то их нужно было бы ортогонализировать с помощью стандартной процедуры). Вектор   к тому же и нормирован. Откуда следует -  . Нормируем теперь вектор : 

   .

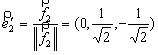 Для случая   уравнение, определяющее собственный вектор есть

    . 

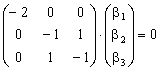Ранг матрицы этой системы уравнений равен 2. Следовательно она имеет одно линейно независимое решение, например,   Отнормируем этот вектор:  .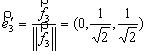

Теперь можно составить искомую матрицу ортогонального преобразования: 

   . 

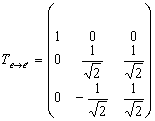Исходная квадратичная форма будет иметь следующий канонический вид

  .

При этом переменные   связаны с переменными   соотношением

   или

 

 

3. Построить в прямоугольной системе координат фигуру, определяемую следующим уравнением, предварительно приведя его к каноническому виду

  .

 Решение. Выделим в этом выражении квадратичную форму  . Это три первых слагаемых уравнения  .

Матрица квадратичной формы равна  . Проведём процедуру приведения квадратичной формы к каноническому виду с помощью ортогонального преобразования. Характеристическое уравнение матрицы имеет вид

  .

Его корни таковы:  .

Найдём теперь собственные векторы, соответствующие этим корням и отнормрируем их. Для вектора  , соответствующего 

, имеем 

    

В итоге собственный вектор, соответствующий  , можно выбрать в виде

  .

Анологичная процедура для собственного вектора  даёт:   

Откуда:

  .

После нормировки полученных векторов имеем:

  .

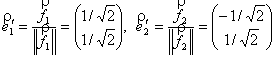Эти векторы представляют собой ортонормированный базис новой системы координат. Матрица ортогонального оператора, приводящего квадратичную форму   к каноническому виду  , есть

 

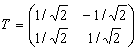
 Связь старых   и новых   координат определяется соотношением  .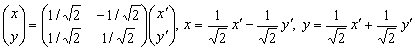

Учитывая приведенные выражения, приведём заданную квадратичную форму к каноническому виду 

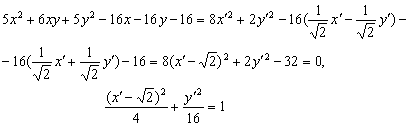Это есть каноническое уравнение эллипса в системе координат  ,которая получается из исходной её поворотом на угол  и переносом начала координат в точку  .