1. Место и роль статистических методов в менеджменте качества

Понятие «управление качеством» как наука возникло в конце 19-го столетия, с переходом промышленного производства на принципы разделения труда. Принцип разделения труда потребовал решения проблемы взаимозаменяемости и точности производства. До этого при ремесленном способе производства продукции обеспечение точности готового продукта производилось по образцам или методами подгонки сопрягаемых деталей и узлов.Учитывая значительные вариации параметров процесса, становилось ясно,что нужен критерий качества производства продукции, позволяющий ограничить отклонения размеров при массовом изготовлении деталей.

В качестве такого критерия Ф.Тейлором были предложены интервалы, устанавливающие пределы отклонений параметров в виде нижних и верхних границ. Поле значений такого интервала стали называть допуском. Установление допуска привело к противостоянию интересов конструкторов и производственников: одним ужесточение допуска обеспечивало повышение качества соединения элементов конструкции, другим – создавалосложности с созданием технологической системы, обеспечивающей требуемые значения вариаций процесса. Очевидно также, что при наличии разрешенных границ допуска у изготовителей не было мотивации «держать» показатели (параметры) изделия как можно ближе к номинальному значению параметра, это приводило к выходу значений параметра за пределы допуска.

В тоже время (начало 20-х годов прошлого столетия) некоторых специалистов в промышленности заинтересовало, можно ли предсказать выход параметра за пределы допуска. И они стали уделять основное внимание не самому факту брака продукции, а поведению технологического процесса, в результате которого возникает этот брак или отклонение параметра от установленного допуска. В результате исследования вариабельности технологических процессов появились статистические методы управления процессами. Родоначальником этих методов был В.Шухарт.

С момента зарождения статистических методов контроля качества специалисты понимали, что качество продукции формируется в результатесложных процессов, на результативность которых оказывают влияние множество материальных факторов и ошибки работников. Поэтому для обеспечения требуемого уровня качества нужно уметь управлять всеми влияющимифакторами, определять возможные варианты реализации качества, научитьсяего прогнозировать и оценивать потребность объектов того или иного качества.

Используемые в сегодняшней практике предприятий статистические методы можно подразделить на следующие категории:

• методы высокого уровня сложности, которые используются разработчиками систем управления предприятием или процессами;

• методы, которые используются при разработке операций технического контроля, планировании промышленных экспериментов,расчетах на точность и надежность и т.д.;

• методы общего назначения, в разработку которых большой вкладвнесли японские специалисты. К ним относятся «Семь инструментов качества», включающие в себя контрольные листки; метод расслоения; графики; диаграммы Парето; диаграммы Исикавы;гистограммы; контрольные карты.

2. Источники статистической информации в менеджменте качества и классификация признаков (величин), характеризующих качество производственных процессов и продукции.

Областью применения вероятностно-статистических методов в менеджменте качества является контроль и управление качеством в сфере производства товаров и предоставления услуг массового потребления.

При этом основными источниками статистической информации в менеджменте качества являются результаты измерения и мониторинга характеристик (величин, признаков), определяющих качество производственных процессов, производимой продукции или предоставляемых услуг.

Таким образом, под характеристикой (величиной или признаком) понимается некоторая характеристика свойства объекта, которую можно измерить, т.е. значение которой можно соотнести с определенным значением на некоторой шкале.

Целью и результатом измерения является отображение интересующих нас свойств объектов эмпирической области на объекты некоторой знаковой области (шкалы).

Типичные признаки, используемые при управлении качеством:

• число/доля дефектных изделий на 100, 1000 или 1000000 (РРМ - единиц на миллион) единиц продукции;

• число дефектов на единицу продукции;

• число/доля превышения сроков (например, исполнения заказа) за единицу времени (день/неделя/месяц/ квартал/год);

• число/доля дней сотрудника на больничном листе за единицу времени (месяц/ квартал/год);

• число/доля рекламаций от заказчика на 100, 1000 выполненных заказов или за определенный период времени (месяц/ квартал/год);

К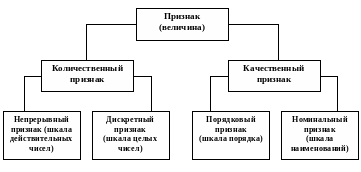 лассификация признаков (величин), характеризующих качество измеряемых объектов:

3. Источники статистической изменчивости данных. Воздействие пяти случайных полей влияния на процесс.

Случай предполагает, что значения измеряемых величин (признаков) рассеиваются, т.е. в каждом отдельном случае могут принимать, вообще говоря, различные значения. Поэтому вероятностно-статистические методы стали неотъемлемой составляющей управления качеством. Определение и правильное применение современных статистических методов имеют важное значение для проведения управляющих воздействий на всех стадиях процессов, осуществляемых в организации.

Статистические методы необходимы, чтобы соответствующим образом описать, представить, сконцентрировать, проанализировать, интерпретировать и использовать для принятия решений результаты измерений величин (признаков), которые подверженные случайному рассеянию и характеризуют качество производственных процессов и их результатов.

Только с помощью статистических методов можно сделать соответствующие адекватные выводы из различных данных, получаемых при измерении и управлении производственными процессами, которые подвержены многочисленным случайным влияниям и воздействиям.

Таким образом, проявляющиеся рассеяния значений измеряемых величин (признаков) можно отнести к многочисленным случайным влияниям и воздействиям, анализ которых привел к их классификации на основных 5 групп, так называемых «5М»:

• Mensch – человек,

• Maschine – машина,

• Material – материал,

• Methode – метод,

• Mitwelt – окружающий мир или окружение.

4. Квантили и интервал случайного рассеивания случайной величины.

Случайная величина – это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.

Функция распределения дает возможность найти вероятность попадания случайной величины в произвольный интервал (открытый или замкнутый) на действительной оси. Иногда возникает обратная задача: найти границы интервала, в который в определенном эксперименте с заданной вероятностью P попадет некоторая случайная величина, имеющая известное распределение вероятностей F_(x).

Таким образом, с понятием Функции распределения вероятностей* тесно связано понятие квантили и интервала случайного рассеивания.

*Функцией распределения вероятностей случайной величины называется функция

F_(x) :R[0, 1], при каждом xR равнаяF_(x) = P(<x) = P{: ()<x }.

Квантиль порядка p или 100р%- ная точка распределения некоторой случайной величины  есть такое значение x_p, для которого P(<x_p) = F_( x_p) = p (0 <p< 1).

И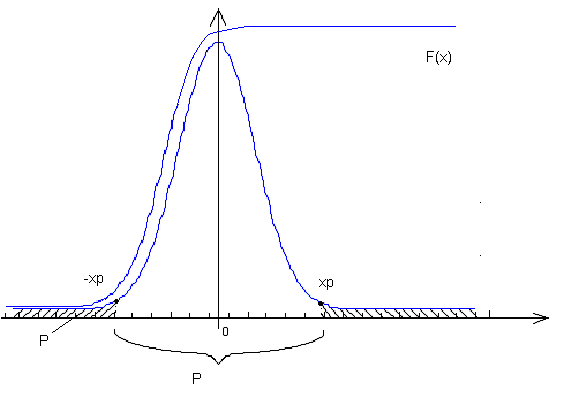 сходя из определения квантиля, он есть функция, обратная к Функции распределения вероятностейF_(x): x_p = F_^-1( p ). Например(см.рисунок)

Квантили позволяют установить так называемые интервалы случайного рассеивания случайной величины или интерквантильные интервалы.

Интервалом случайного рассеивания или интерквантильным интервалом случайной величины , соответствующим доверительной вероятности Pназывается интервал на действительной оси (x_p, x_p+P), вероятность попадания в который случайной величины  в каждом эксперименте равна P где x_p, x_1-p – квантили случайной величины , при этом p = (1-P)/2, p+P=(1+P)/2.

Для определенности, обычно при построении интервалов случайного рассеивания, вероятности попадания случайной величины в «хвосты» распределения полагаются равными.

5.Математическое ожидание и дисперсия дискретной и непрерывной случайных величин и их свойства.

Математическое ожидание

Математическим ожиданием дискретной случайной величины называется сумма произведений ее возможных значений на соответствующие им вероятности: М(Х) = х₁р₁ + х₂р₂ + … + х_пр_п , если полученный ряд сходится абсолютно.

МатОжид.НеперерывнойСВ- Математическим ожиданием E случайной величины  с абсолютно непрерывным распределением с плотностью распределения f_(x) называется число

(Бонус), на всякий.

Математическое ожидание (МО) имеет простой физический смысл: если на прямой разместить единичную массу, поместив в точки x_i массу p_i (для дискретного распределения), или «размазав» ее с плотностью f_(x) (для абсолютно непрерывного распределения), то точка E есть координата «центра тяжести» распределенной единичной массы.

Свойства математического ожидания

Если математические ожидания существуют, то имеют место следующие свойства

1. Для произвольной функции g (ξ): rr:

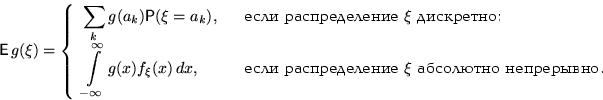
2. Математическое ожидание постоянной равно этой постоянной:

Ec = c.

3. Постоянную можно вынести за знак математического ожидания: .

4.  Математическое ожидание суммы любых случайных величин  и  равно сумме их математических ожиданий:

5. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: если  и  независимы, то .

Дисперсия

Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата ее отклонения от ее математического ожидания: (определение одно для обоих)

D(X) = M (X — M(X))².-дискретная СВ

непрерывная СВ

Свойства дисперсии.

1)Дисперсия постоянной величины С равна нулю:

D (C) = 0.

2)Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:

D(CX) = C²D(X).

3)Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:

D(X + Y) = D(X) + D(Y).

4)Дисперсия разности двух независимых случайных величин равна сумме их дисперсий::

D(X — Y) = D(X) + D(Y).

5) Дисперсия не отрицательная.

6) Если дисперсия случайной величины конечна, то конечно и её математическое ожидание

6. Примеры распределений, используемых в задачах менеджмента качества, их распределения и параметры (Биномиальное распределение, распределение Пуассона, нормальное распределение, равномерное распределение и др.).

При помощи распределения описывается взаимосвязь между возможными значениями случайной величины и вероятностями, относящимися к этим значениям.

Наиболее часто в менеджменте качества используются модели следующих распределений:

• Биномиальное распределение для дискретных случайных величин типа «числа бинарных/двойных значений признака на выборку».

• распределение Пуассона для дискретных случайных величин типа «числа событий на рассматриваемую единицу»

• нормальное распределение для непрерывных случайных величин

• равномерное распределение.

С помощью статистических методов можно описать случайные воздействия и, в определенной степени, предсказать и спрогнозировать ожидаемые в будущем результаты.

Биномиальный закон распространяется на последовательность независимых испытаний, каждое из которых имеет лишь два возможных исхода, которые обычно условно называют «успех» или «неуспех». Причем считается, что вероятность «успеха» в каждом испытании известна, постоянна и равна p, тогда, очевидно вероятность «неуспеха» q = 1 – p.

Можно показать, что случайная величина  имеет биномиальное распределение с параметрами (n, p) (0 < p < 1, n ≥ 1), если вероятность ее принять конкретное значение 0 ≤ k ≤ n, определяется формулой: P = C_n^k p^k(1 – p)^{n – k}

Биномиальный закон применяется для:

• определения выборки, позволяющей осуществить приемку по альтернативным признакам (число бракованных изделий);

• управления процессом "р" (процент брака).

Биномиальный закон распределения относится к случаям, когда была сделана выборка фиксированного объема. Распределение Пуассона относится к случаям, когда число случайных событий происходит на определенных длине, площади, объеме или времени, при этом определяющим параметром распределения является среднее число событий m, а не объем выборки n и вероятность успеха p. Распределение вероятностей для числа успехов x имеет при этом следующий вид: P(x)=[m^x/x]e^-m.

Закон Пуассона распространяется на «редко» происходящие события, при этом возможность очередной удачи (например, сбоя) сохраняется непрерывно, является постоянной и не зависит от числа предыдущих удач или неудач (когда речь идет о процессах, развивающихся во времени, это называют "независимостью от прошлого"). Классическим примером, когда применим закон Пуассона, является число телефонных вызовов на телефонной станции в течение заданного интервала времени. Другими примерами могут быть число чернильных клякс на странице, неаккуратно написанной рукописи, или число соринок, оказавшихся на кузове автомобиля во время его окраски. Закон распределения Пуассона измеряет число дефектов, а не число бракованных изделий.

Приложениями распределения Пуассона являются:

• определение выборки, позволяющей осуществить приемку по альтернативным признакам (число бракованных изделий);

• управление процессом "с" (число дефектов).

Нормальное распределение – это основной закон статистики. Он выделяется своим фундаментальным значением среди остальных распределений. Ему подчиняются непрерывные случайные величины x, значения которых зависит от большого числа случайных воздействий. Это в равной степени могут быть случайные ошибки эксперимента и множество случайных воздействий на технологический процесс. Важным для практики свойством нормального закона является то, что он является хорошей аппроксимацией биномиального и пуассоновского распределений при достаточно больших _n и _np. Распределение вероятностей для среднего значения выборки обычно близко к нормальному закону даже, если отдельные выборочные значения xi распределены существенно иным образом.

П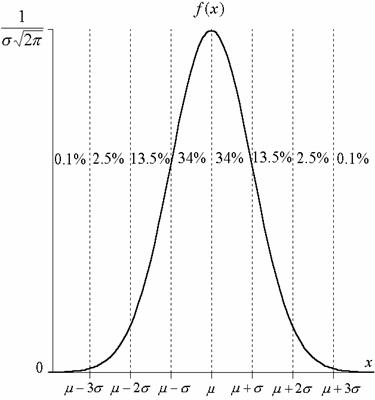 лощадь под Гауссовой кривой _f(x) равна единице. Числа указывают доли площади (в % ) в соответствующей полосе под кривой _f(x). Это приближенные значения, округленные так, чтобы их было легче запомнить.

Для нормально распределенной случайной величины вероятность оказаться в полосе от среднего равна 68%, вероятность выхода за пределы полосы составляет приблизительно 5% ,и только в 0.27% случаев процесс может выйти за пределы . Умножая плотность распределения вероятности на общую численность совокупности N можно перейти к плотности распределения частоты.

Непреры́вное равноме́рное распределе́ние — в теории вероятностей распределение, характеризующееся тем, что вероятность любого интервала зависит только от его длины. F(x)=

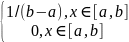
Биномиальное

M = Np, D = Np(1-p)

Пуассона

один параметр  = M = D

Нормальное

a= M, ² = D

Равномерное

M = (а+b)/2

D = (b-a)²/12

8. Оценивание характеристик корреляции и регрессии в задачах менеджмента качества.

Корреляционная зависимость возникает тогда, когда один из признаков зависит не только от второго, но и от ряда случайных факторов или условий, от которых зависят оба фактора. Корреляционные связи не могут рассматриваться как свидетельство причинноследственной зависимости. Они свидетельствуют лишь о том, что изменения одного признака, как правило, соответствуют определенному изменению другого. При этом неизвестно, находится ли причина изменений в одном из признаков или она оказывается за пределами исследуемой пары признаков.

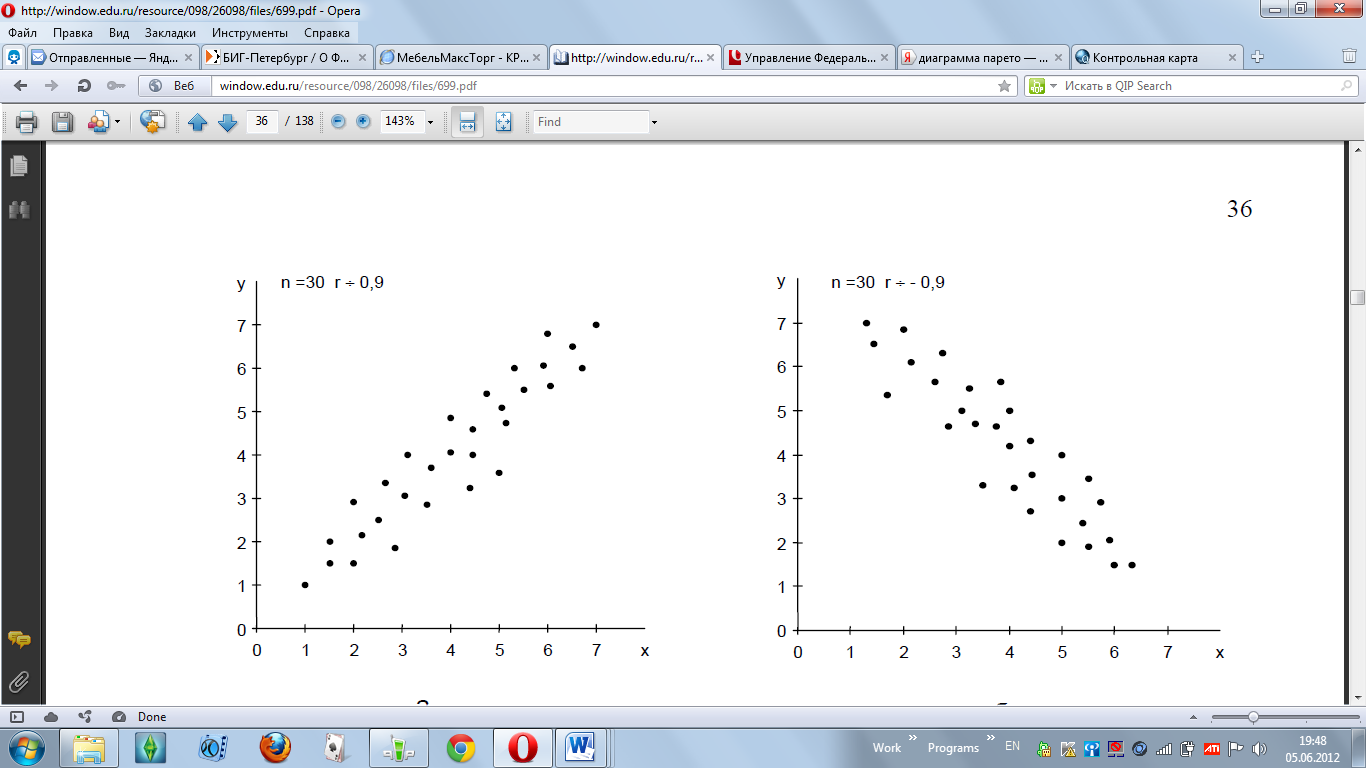
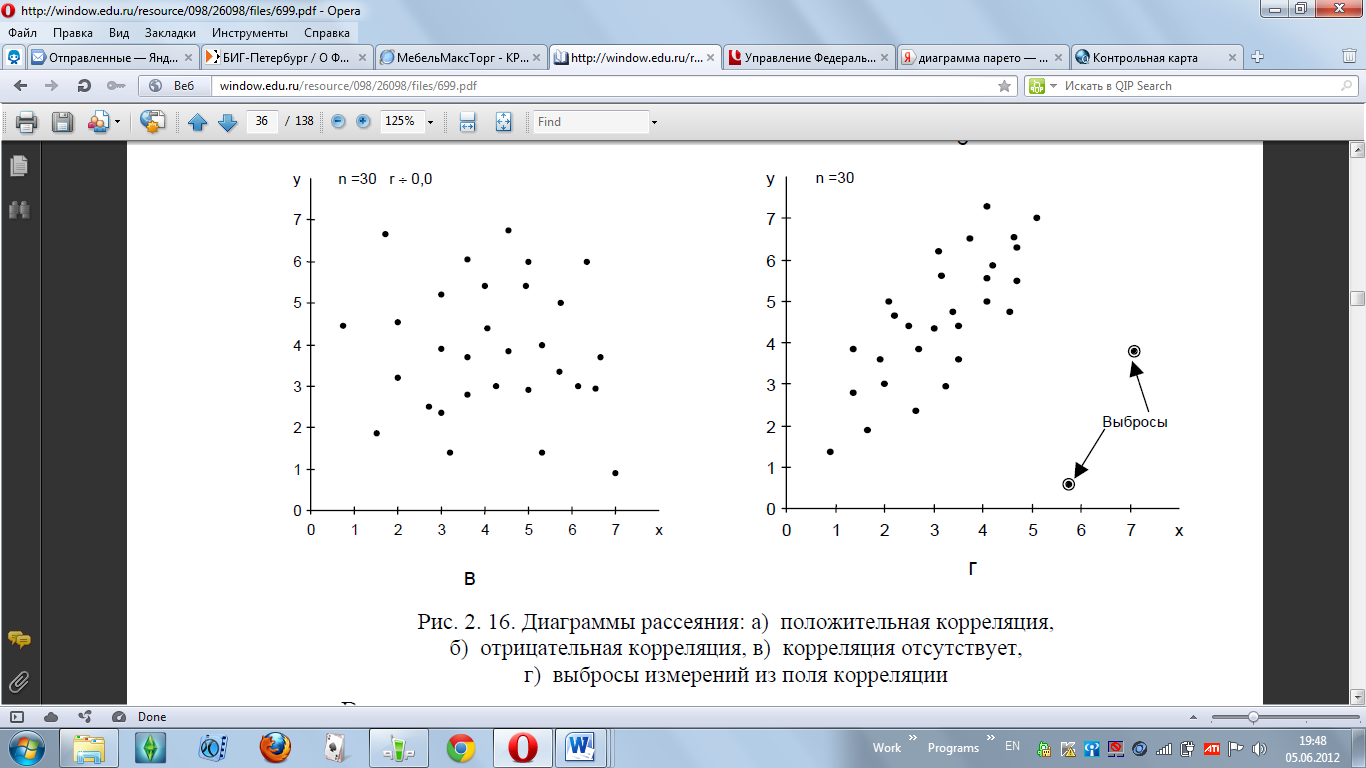
Виды корреляционных связей между измеренными признаками могут быть линейными и нелинейными, положительными или отрицательными.

Варианты корреляционных связей отражены на рис. Возможна также ситуация, когда между переменными невозможно установить какую - либо зависимость. В этом случае говорят об отсутствии корреляционной связи.

В задачи корреляционного анализа входит:

- установление направления (положительное или отрицательное) и формы (линейная или нелинейная) связи между варьирующими признаками,

- измерение тесноты связи (значения коэффициентов корреляции),

- проверка уровня значимости коэффициентов корреляции.

Корреляционную зависимость между переменными X и Y можно выразить с помощью уравнений типа Yх = F(x) или Xy = F(Y) , которые называются уравнениями регрессии. В этих уравнениях Yx и Xy являются средними арифметическими переменных X и Y.

Графическое выражение регрессионного уравнения называют линией регрессии. Линия регрессии выражает наилучшее предсказание зависимой переменной Y по независимым переменным X.

+ добавить про кор.отношение, крамера….ОБЯЗАТЕЛЬНО!!!!!!!!!!!!!!!!!!!!!!! И ПРИМЕРЫ!!!!!!!!!!