23.Вертикальные и наклонные асимптоты функции.

Определение. Прямая А называется асимптотой кривой, если расстояние δ от переменной точки М кривой до этой прямой при удалении точки М в бесконечность стремится к нулю.

Вертикальные асимптоты.

Из определения асимптот следует, что если

lim f(x) = бесконечность или lim f(x) = бесконечность

x→a+0 x→a-0

или lim f(x) = бесконечность.

Х→a

то прямая х = а есть асимптота кривой y = f(x); и обратно, если прямая х = а есть асимптота, то выполняется одно из написанных равенств.

Следовательно, для нахождения вертикальных асимптот нужно найти такие значения х = а, при приближении к которым функция y = f(x) стремится к бесконечности. Тогда прямая x = a будет вертикальной асимптотой.

Наклонные асимптоты.

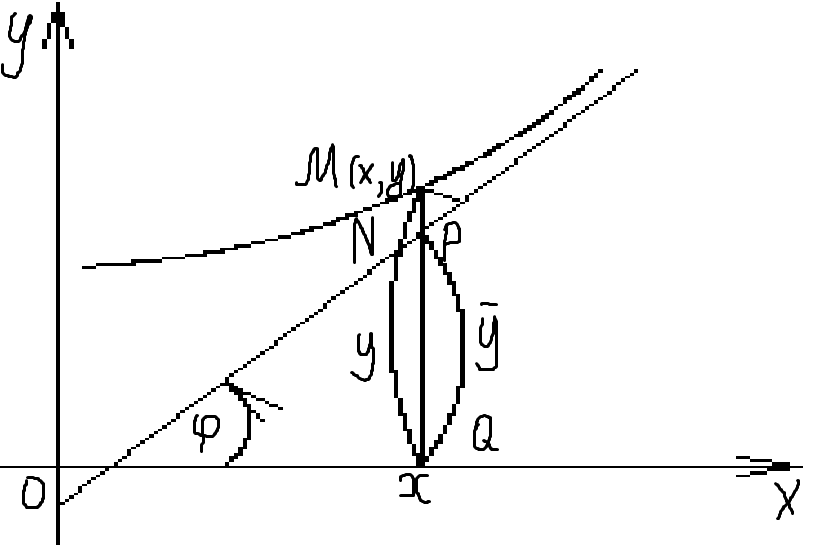
Пусть кривая f(x) имеет наклонную асимптоту, уравнение которой имеет вид y = kx + b. Определим числа k и b. Пусть M (x, y) – точка, лежащая на кривой, и N (x, y) – точка, лежащая на асимптоте. Длина отрезка [MP] равна расстоянию точки M до асимптоты. По условию lim |MP| = 0

х → + бесконечность

Если обозначим через φ угол наклонной к оси Ох, то из ∆NMP найдем:

|NM| = |MP|/cosφ

Так как φ – постоянный угол (не равный п/2), то в силу предыдущего равенства

lim |MN| = 0 и наоборот

x→+бесконечность

Но: |NM| = ||QM| - |QN|| = |y – y(вектор)| = |f(x) – (kx + b)|

и равенство принимает вид: lim [f(x) – kx – b] = 0

x→+бесконечность.

Определим теперь k и b. Вынося х за скобки в равенстве, получаем:

lim x [(f(x))/x – k – b/x] = 0.

Х→+бесконечность

Так как х→+бесконечности, то должно выполняться равенство:

lim [(f(x))/x – k – b/x] = 0.

X→+бесконечность

При b постоянном lim b/x = 0. Следовательно, lim [(f(x))/x – k] = 0.

X→+бесконечность х→+бесконечность

Или k = lim (f(x))/x

х→+бесконечность

Зная k, из равенства находим b:

b = lim [(f(x)) – kx]

x→+бесконечности

Все рассуждения так же справедливы, если х стремится к минус бесконечности.

24. План исследования функции. Построение графиков функции.

План исследования функции:

1. Область определения.

Чётность, нечётность. (f(-x)=f(x) – чётная; f(-x)=-f(x) – не чётная.)

Периодичность.

Интервалы знакопостоянства. Нули функции.

2. Исследование на непрерывность.

Точки разрыва и их классификация.

Вертикальная асимптота.

3. Исследование на монотонность.

Экстремумы.

4. Исследование на выпуклость и вогнутость.

Точки перегиба.

5. Наклонные асимптоты.

6. Эскиз графика.

На основание проведенного исследования строится график функции (иногда целесообразно намечать элементы графика параллельно исследованием.

Если исследуемая функция y=f(x) – чётная, т.е. такая, что при изменении знака аргумента значение функции не изменяется, т.е. если f(-x) = f(x), то достаточно исследовать функцию и построить её график при положительных значениях аргумента, принадлежащих области определения функции. При отрицательных значениях аргумента график функции строится на том основании, что график чётной функции симметричен относительно оси ординат.

Функция y = x² – чётная, так как (-x)² = x²

Функция y = cos x – чётная, так как cos(-x) = cos x.

Если функция y = f(x) – нечётная, т.е. такая, что при изменении аргумента функция меняет знак, т.е. если f(-x) = -f(x), то эту функцию достаточно исследовать при положительных значениях аргумента. График нечётной функции симметричен относительно начала координат.

Функция y = x³ – нечётная, так как (-х³) = -х³

Функция y = sin x – нечетная, так как sin(-x) = -sin x.

Так как знание одних свойств функции позволяет сделать вывод о других ее свойствах, то иногда порядок исследования целесообразно выбирать, исходя из конкретных особенностей данной функции. Так, например, если мы выяснили, что заданная функция непрерывна и дифференцируема, и нашли точки максимума и минимума этой функции, то тем самым мы уже определили и области возрастания и убывания функции.