7. Методы инициализации весов
Обучение нейронных сетей представляет собой трудоемкий процесс, далеко не всегда дающий ожидаемые результаты. Проблемы возникают из-за нелинейных функций активации, образующих многочисленные локальные минимумы, к которым может сводиться процесс обучения. Применение методов глобальной оптимизации уменьшает вероятность остановки процесса обучения в точке локального минимума, однако платой за это становится резкое увеличение трудоемкости и длительности обучения. Для правильного подбора управляющих параметров требуется большой опыт.
На результаты обучения огромное влияние оказывает подбор начальных значений весов сети. Выбор начальных значений, достаточно близких к оптимальным, значительно ускоряет процесс обучения. К сожалению, не существует универсального метода подбора весов, который бы гарантировал нахождение наилучшей начальной точки для любой решаемой задачи.
Неправильный
выбор диапазона случайных значений
весов может вызвать слишком раннее
насыщение нейронов, в результате
которого, несмотря на продолжающееся
обучение, среднеквадратичная погрешность
будет оставаться практически постоянной.
Явления такого типа означают попадание
в седловую зону целевой функции вследствие
слишком больших начальных значений
весов. При этом взвешенная сумма входных
сигналов нейрона может иметь значение,
соответствующее глубокому насыщению
сигмоидальной функции активации. При
этом поляризация насыщения обратна
ожидаемой. Значение возвратного сигнала,
генерируемое в методе обратного
распространения, пропорционально
величине производной от функции активации
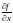, в точке насыщения близко нулю. Поэтому
изменения значений весов, выводящие
нейрон из состояния насыщения, происходит
очень медленно. Процесс обучения надолго
застревает в седловой зоне. Нейрон,
остающийся в состоянии насыщения, не
участвует в преобразовании данных,
сокращая таким образом эффективное
количество нейронов в сети. В итоге
процесс обучения чрезвычайно замедляется,
поэтому состояние насыщения отдельных
нейронов может длиться практически
непрерывно вплоть до исчерпания лимита
итераций.
Удаление
стартовой точки активации нейронов от
зоны насыщения достигается путем
ограничения диапазона случайных
значений. Почти все оценки нижней и
верхней границ диапазона допустимых
значений лежат в интервале (0,1). В одной
из недавних работ предложено равномерное
распределение весов, нормализованное
для каждого нейрона по амплиту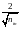де
,
где
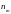означает количество входов нейрона.
Веса порогов для нейронов скрытых слоев
должны принимать случайные значения
из интервала
,
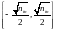а для выходных нейронов - нулевые
значения.
Алгоритм обучения персептрона (Теорема о сходимости персептрона)
Чтобы вывести алгоритм обучения персептрона, основанный на коррекции ошибок, рассмотрим модель элементарного персептрона с m входами, смещением b и функцией активации hardlim. На n-ном шаге итерации входной вектор имеет вид
.
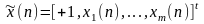Вектор весовых коэффициентов:
.
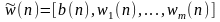Выход линейного сумматора :
.
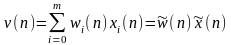При фиксированном
значении n уравнение
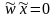определяет гиперплоскость в m-мерном
пространстве для некоторого значения
порога b, которая является поверхностью
решений для двух различных классов
входных сигналов. Чтобы персептрон
функционировал корректно, классы должны
быть линейно разделимыми.
Предположим, что выборки,
используемые для обучения, принадлежат
двум линейно разделимым классам С1 и
С2.
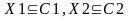– множества обучающих сигналов. Требуется
так настроить веса, чтобы
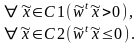
При определенных таким
образом подмножествах Х1 и Х2 задача
обучения элементарного персептрона
сводится к нахождению такого вектора
весов
,
для которого выполняются указанные
неравенства. Если вход
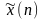классифицирован правильно, то вектор
весов не корректируется. В противном
случае веса корректируются в соответствии
с правилом:
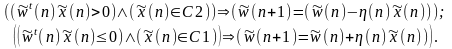
Если
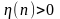– константа, не зависящая от n, вышеописанный
алгоритм называется правилом адаптации
с фиксированным приращением (fixed increment
adaptation rule). Приведем без доказательства
теорему сходимости персептрона с
фиксированным приращением.
Пусть
подмножества Х1 и Х2 линейно разделимы.
Пусть входные сигналы поступают только
от этих подмножеств. Тогда алгоритм
обучения персептрона сходится после
конечного числа
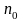итераций в том смысле, что
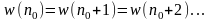является вектором решения для
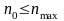
Рассмотренный алгоритм адаптации вектора весовых коэффициентов соответствует правилу обучения на основе коррекции ошибок (error-correction learning rule)
.
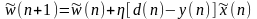Параметр скорости
обучения является константой,
.
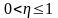Выбирая значение
следует учитывать взаимоисключающие
требования:
усреднение (averaging) предыдущих входных сигналов, обеспечивающее устойчивость оценки вектора весов, требует малых значений ,
быстрая адаптация (fast adaptation) к реальным изменениям параметров процесса, отвечающего за формирование векторов входного сигнала, требует больших значений .
Обучение нейронной сети
Для построения и обучения нейронной сети обычно создается набор примеров, который представляет собой совокупность векторов вида (Х,У), где Х = (х1х2, ... , хn) - значения всех входов нейронной сети, а У = (у1, у2, ... , уn)-значения всех выходов нейронной сети, которые должны получаться в процессе ее работы. Структура эталонных векторов задает одновременно количество входных и выходных нейронов (в данном случае n и m соответственно).
Целью обучения нейронной сети является достижение такой ситуации, когда при подаче на вход сети любого вектора X из набора примеров на ее выходе получается выходной вектор У’, отличающийся от эталонного вектора У не более чем на заданную заранее и вычисляемую определенным образом величину .
Процесс обучения нейронной сети заключается в подборе значений всех ее характеристик таким образом, чтобы отличия выходных векторов от эталонных не превышали заранее установленной величины.
Основными характеристиками нейронной сети являются:
количество скрытых слоев,
количество нейронов в каждом из скрытых слоев,
веса входов каждого из скрытых и выходных нейронов wij,
функция активации F(neti) для каждого скрытого и выходного нейрона.
Таким образом, мы можем обобщенно сформулировать оптимизационную задачу обучения нейронной сети. Исходными данными для нее будут:
количество входных и выходных нейронов,
количество настраиваемых весов,
набор обучающих примеров.
В результате решения этой задачи мы должны получить следующие значения:
количество скрытых слоев,
количество нейронов в каждом скрытом слое,
значения весов всех входов для каждого скрытого и выходного нейрона,
функции активации для каждого скрытого и выходного нейрона.
Очевидно, что целевой функцией в данном случае будет отличие выходного вектора У’ от эталонного У, определяемая как
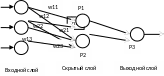
Рисунок 1. Нейронная сеть
Сеть состоит из шести нейронов и имеет один скрытый слой. Используется Сигмоидная активационная функция:
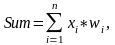
где n –число входов нейрона, xi – значение i-го входа, wi – вес i-го входа, Р – параметр функции активации, определяющий ее крутизну. Чем больше Pi, тем ближе сигмоида приближается к пороговой функции.
Векторы параметров сети будут иметь вид (x1,x2,x3,x4,y1), где xi – входы, а y1 – выход сети.
В качестве целевой функции будем рассматривать
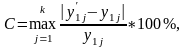
где k – количество
примеров,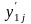
- выход нейронной сети для j-го примера,
y1j - эталонное значение выхода НС.