1.Понятие числового ряда, необходимый признак сходимости ряда:

-что такое ряд

Это сумма бесконечной числовой последовательности. Бесконечная числовая последовательность –числовой ряд

-сходящий и расходящийся ряд.

Ряд сходится, если существует конечный предел его частичной суммы

Ряд расходится, если этот предел равен бесконечности

-свойства сходящихся рядов

Если ряд сходится, то сходится любой из его остатков. Наоборот, из сходимости какого-то остатка вытекает сходимость всего ряда. Отсюда следует, что изменение или выбрасывание конечного числа членов ряда не изменяет его сходимости или расходимости.

Если ряд   сходится, то  .

Если ряд   сходится, то сходится ряд   и имеет место равенство

.

Если ряды   и   сходятся, то сходится и ряд    имеет место равенство

.

Если ряд   сходится, то  .

Отсюда следует

Признак расходимости ряда. Если  , то ряд   расходится.

-понятие частичной суммы

Частичная сумма – ограниченная

Sn= a₁ +a₂+ . . . +a_n

a_n – общий член ряда

2. признаки сходимости знакоположительных рядов

- признак сравнений

- признак сравнения в предельной форме

3. признак Даламбера и радикальный признак Коши (интегральный)

4. Знакопеременные ряды.

- понятие условной сходимости и понятие абсолютной сходимости

- теорема об абсолютной сходимости

5. Знакочередующие ряды

- признак Лейбница

6. Функциональные ряды

- признак сходимости функционального ряда

- теорема Вейштрасе

7. Степенные ряды

- теорема Абеля

Теорема. Если степенной ряд   сходится при x = x₁ , то он сходится и притом абсолютно для всех  .

 

  Доказательство. По условию теоремы, так как члены ряда ограничены, то

где k- некоторое постоянное число. Справедливо следующее неравенство:

Из этого неравенства видно, что при x<x₁ численные величины членов нашего ряда будут меньше ( во всяком случае не больше ) соответствующих членов ряда правой части записанного выше неравенства, которые образуют геометрическую прогрессию. Знаменатель этой прогрессии   по условию теоремы меньше единицы, следовательно, эта прогрессия представляет собой сходящийся ряд.

Поэтому на основании признака сравнения делаем вывод, что ряд   сходится, а значит ряд   сходится абсолютно.

 

Таким образом, если степенной ряд  сходится в точке х₁, то он абсолютно сходится в любой точке интервала длины 2 x₁ с центром в точке х = 0.

 

Следствие. Если при х = х₁ ряд расходится, то он расходится для всех  .

8. Радиус сходимости, область, интервал сходимости степенного ряда

Если интервал сходимости представляется в виде  , где R > 0, то величина R называется радиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно.  Радиус сходимости можно вычислить, воспользовавшись радикальным признаком Коши, по формуле

или на основе признака Даламбера:

области сходимости ряда:

– Если установлено, что степенной ряд расходится на обоих концах интервала, то область сходимости ряда совпадает с интервалом сходимости: (a,b)

– Если установлено, что степенной ряд сходится на одном конце интервала и расходится на другом, то область сходимости ряда представляет собой полуинтервал: [a, b) или (a, b]

– Если установлено, что степенной ряд сходится на обоих концах интервала, то область сходимости ряда представляет собой отрезок: [a, b]

Термины очень похожи, область сходимости ряда – это чуть более детализированный интервал сходимости ряда.

Число R такое, что при степенной ряд сходится, при ряд расходится, называется радиусом сходимости. Интервал называется интервалом сходимости степенного ряда.

9. Ряды Фурье

- понятие, что такое ряды Фурье и как найти коэффициенты разложение в ряд Фурье

Коэффициенты, определяемые по формулам

, , , называются коэффициентами Фурье функции  , а тригонометрический ряд с такими коэффициентами называется рядом Фурье функции  .

Говорят, что функция f (x) имеет период P, если f (x + P) = f (x) для всех значений x. Пусть период функцииf (x) равен 2π. В этом случае достаточно рассмотреть поведение функции в интервале [−π, π]. 

1. Предположим, что функция f (x) с периодом 2π абсолютно интегрируема в интервале [−π, При этом является конечным так называемый интеграл Дирихле:

2. Предположим также, что функция f (x) является однозначной, кусочно-непрерывной (то есть имеет конечное число точек разрыва) и кусочно-монотонной (имеет конечное число максимумов и минимумов).

Если условия 1 и 2 выполнены, то ряд Фурье для функции f (x) существует и сходится к данной функции (Смотрите об условиях сходимости также раздел Сходимость рядов Фурье).  Если x₀ − точка разрыва, то ряд Фурье сходится к значению

Ряд Фурье функции f (x) представляется в виде

где коэффициенты Фурье a₀, a_n и b_n определяются формулами

Иногда используются альтернативные формы записи для разложения в ряд Фурье. Заменяя a_n и b_n новыми переменными d_n и φ_n или d_n и θ_n , где

можно, соответственно, записать

10. Дифференцирование функций двух переменных

- дифференцирование сложной функции

Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке  , а функция g имеет производную в точке  , то сложная функция h(x) = g(f(x)) также имеет производную в точке .

- дифференцирование неявно заданной функции 2-ух переменных

Функция z = ƒ (х; у) называется неявной, если она задается уравнением

неразрешенным относительно z. Найдем частные производные   неявной функции z, заданной уравнением (44.11). Для этого, подставив в уравнение вместо z функцию ƒ (х; у), получим тождество F(x;у;ƒ (х; у)) = 0. Частные производные по х и по у функции, тождественно равной нулю, также равны нулю:

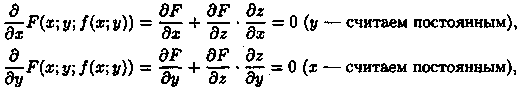
Откуда

Имеет место теорема существования неявной функции двух переменных: если функция F(x; у; z) и ее производные F'x(x; у; z), F'y(x; у; z), F'z(x;y;z) определены и непрерывны в некоторой окрестности точки M0(x₀;y₀;z₀), причем F(x₀;y₀;z₀)=0, а F'z(x₀;y₀;z₀)≠0, то существует окрестность точки М₀, в которой уравнение (44.11) определяет единственную функцию z=ƒ(х;у), непрерывную и дифференцируемую в окрестности точки (х₀;у₀) и такую, что ƒ(х₀;у₀)=z₀.

- двойное дифференцирование (вычисление двойной производной)