
- •Основные понятия теории вероятностей
- •1 Построить графики интегральной и дифференциальной функций распределения для нормального, равномерного и любого на выбор законов распределения для разных объемов выборок.
- •1.4.1 Дифференциальная и интегральная функции распределения для первой выборки
- •2 Считать, что есть экспериментальные данные, провести анализ: построить гистограмму, определить основные характеристики.
- •3 Доказать гипотезу о виде закона распределения, используя известные критерии согласия.
1.4.1 Дифференциальная и интегральная функции распределения для первой выборки
i = 0


(экспоненциальный закон)

(экспоненциальный закон)
1.4.2 Дифференциальная и интегральная функции распределения для второй выборки


(экспоненциальный закон)

(экспоненциальный закон)

i = 2
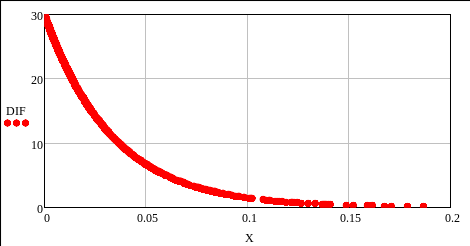
(экспоненциальный закон)

(экспоненциальный закон)
2 Считать, что есть экспериментальные данные, провести анализ: построить гистограмму, определить основные характеристики.
2.1 Построим гистограмму для третьей выборки нормального закона распределения, для этого «Type: = n», и i:=2 - номер выборки.
Найдем минимальное и максимальное значения выборки (XMAX и XMIN), ее длину (L), оптимальное число интервалов группирования вариант (K) и шаг гистограммы (SHAG):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() - частота попаданий в
интервалы
- частота попаданий в
интервалы
|
|
Поострим гистограмму относительных интервальных частот otnositChastot:
![]()

2.3 Определение основных характеристик
Определим основные характеристики выборки: мат. ожидание МХ, дисперсию DX, среднее квадратическое отклонение σХ:
3 Доказать гипотезу о виде закона распределения, используя известные критерии согласия.
По внешнему виду полученной гистограммы можно выдвинуть гипотезу о принадлежности выборки нормальному закону распределения. Проверим эту гипотезу с помощью критерия согласия Пирсона.
Найдем середины интервалов группирования
выборки serinterj,
а также значения
 и
и
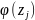 :
:
![]()
![]()

Найдем теоретические частоты:
![]()
Проверим выполнение условия
 :
:
![]()
Условие выполняется, т. к.
 = 810.
= 810.
Проверка гипотезы критерием согласия Пирсона:
Посчитаем наблюдаемое значение χ2:

 .
Для этого зададим уровень значимости
.
Для этого зададим уровень значимости
 .
Число степеней свободы
.
Число степеней свободы
 .
Значение
.
Значение
 найдем по таблице распределения
найдем по таблице распределения
 .
.
![]()
![]()
![]()
4.
Задача: построить модель колебательной
системы считая, что выход
 ,
,
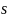 – номер отсчета,
– номер отсчета,
 – шум с нулевым средним и единичной
дисперсией,
– шум с нулевым средним и единичной
дисперсией,
 – вычисляется по заданной величине
отношения сигнала к шуму.
– вычисляется по заданной величине
отношения сигнала к шуму.
Уравнение вынужденных колебаний описывается выражением:
 (1)
(1)
Зададим параметры
 следующим образом:
следующим образом:
 ,
, ,
,
 ,
,
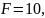

 .
Задаем начальные условия:
.
Задаем начальные условия:
 ,
,
 .
Решив уравнение (1) при заданных параметрах,
получим график функции
.
Решив уравнение (1) при заданных параметрах,
получим график функции
 ,
которая будет описывать зависимость
ускорения системы от времени.
,
которая будет описывать зависимость
ускорения системы от времени.

После наложение шума с нормальным
законом распределения, получим модель
выхода датчика ускорения
 .
.

Вывод: в ходе лабораторной работы я повторили основные понятия и принципы теории вероятностей: случайные величины, законы распределения случайных величин, основные характеристики случайных величин, принцип построения гистограмм, метод проверки статистических гипотез с помощью критериев согласия. Построил модель колебательной системы с использованием случайной величины – шума.
Ответы на контрольные вопросы
1. Дайте определение и приведите примеры случайных величин?
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.
Случайные величины, принимающие только отделенные друг от друга значения, которые можно заранее перечислить, называются случайными дискретными величинами. Случайные величины, возможные значения которых непрерывно заполняют некоторый промежуток, называются случайными непрерывными величинами.
Примерами случайных величин может являться скорость броуновской частицы.
2. Что такое “закон распределения “ случайной величины? Приведите примеры.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Примерами законов распределения случайных величин являются нормальный, равномерный, биномиальный законы.
3. Поясните смысл функции распределения случайной величины. Приведите примеры.
Функция распределения случайной величины F(x) равна вероятности того, что случайная величина Х примет значение, меньшее х: F(x) = P(X < х)
Например, F(-∞) = 0, а F(∞) = 1, так как случайная величина не может быть меньше минус бесконечности и всегда меньше плюс бесконечности
4. Поясните смысл плотности распределения величины. Приведите примеры.
Плотность распределения f(x) – величина, которая характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Например, для нормального распределения
 .
.
5. Как связаны между собой функции распределения и плотность распределения случайной величины?
Функции распределения и плотность распределения случайной величины связаны между собой формулой:
F`(x) = f(x)
6. Какие числовые характеристики случайной величины Вы знаете? Приведите примеры.
Характеристики случайной величины: мат. ожидание МХ, дисперсия DX, СКО σХ, мода, медиана Ме, асимметрия As, эксцесс Ek.
7. Как определить закон распределения случайной величины на основе опытных данных?
Закон распределения случайной величины определяется на основе опытных данных с помощью критериев согласия. Предварительно для этого строится гистограмма или полигон частот. Также можно выдвинуть гипотезу о законе распределения по численным значениям асимметрии и эксцесса.
8. Приведите методику построения гистограмм. Для каких целей используется гистограмма распределения случайной величины?
Гистограмма строится следующим образом. По оси абсцисс откладываются разряды, и на каждом из разрядов как их основании строится прямоугольник, площадь которого равна частоте данного разряда. Для построения гистограммы нужно частоту каждого разряда разделить на его длину и полученное число взять в качестве высоты прямоугольника. В случае равных по длине разрядов высоты прямоугольников пропорциональны соответствующим частотам. Из способа построения гистограммы следует, что полная площадь её равна единице.
6. Мат ожидание свойства
![]()
1) Математическое ожидание постоянной величины равно самой постоянной.
2) Постоянный множитель можно выносить за знак математического ожидания.
3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий. Это свойство справедливо для произвольного числа случайных величин.
4) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых.
7.Дисперсия св.
Дисперсия характеризует степень рассеяния значений случайной величины относительно её математического ожидания.
Дисперсия
случайной величины — это математическое
ожидание квадрата отклонения случайной
величины от её математического ожидания.
![]()
Св-ва:
1) Дисперсия постоянной величины равна нулю.
2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.
3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.
4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.
8. Начальным моментом k-го порядка случайной величины x называется математическое ожидание k-й степени случайной величины x , т.е. a k = Mx k.
Центральным моментом k-го порядка случайной величины x называется величина m k, определяемая формулой m k = M(x - Mx )k
9. Ген. Совокупность – совокупность всех объектов относительно которых учёный намерен делать выводы при изучении.
Выборка - Часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение обо всей генеральной совокупности
10. Гистограмма - По оси абсцисс откладываются разряды, и на каждом из разрядов как их основании строится прямоугольник, площадь которого равна частоте данного разряда. Для построения гистограммы нужно частоту каждого разряда разделить на его длину и полученное число взять в качестве высоты прямоугольника.
Полиго́н часто́т — один из способов графического представления плотности вероятности случайной величины. Представляет собой ломаную, соединяющую точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов.
11. Выборочная дисперсия — это оценка теоретической дисперсии распределения на основе выборки.
12.Ассиметрия
- величина,
характеризующая
асимметрию распределения данной случайной
величины.
![]() Эксцесс -
Эксцесс -
![]() мера
остроты пика.
мера
остроты пика.
13. ТОЧЕЧНАЯ ОЦЕНКА - оценка имеющая конкретное числовое значение.
--Оценка ![]() называется несмещённой,
если её математическое ожидание равно
оцениваемому параметру генеральной
совокупности:
называется несмещённой,
если её математическое ожидание равно
оцениваемому параметру генеральной
совокупности:
--Оценка ![]() называется эффективной,
если она обладает минимальной дисперсией
среди всех возможных несмещенных
точечных оценок.
называется эффективной,
если она обладает минимальной дисперсией
среди всех возможных несмещенных
точечных оценок.
--Оценка ![]() называется состоятельной,
если она по вероятности с увеличением
объема выборки n стремится к параметру
генеральной совокупности:
называется состоятельной,
если она по вероятности с увеличением
объема выборки n стремится к параметру
генеральной совокупности: ![]() ,
,
![]() по
вероятности при
по
вероятности при ![]()
14.Стат гипотеза – всякое предположение о генеральной совокупности, проверяемое по выборке. Проверка гипотезы – критерий значимости – ошибка 1 рода.
15. Ошибки 1 рода – отвергнуть правильную гипотезу(уровень значимости), 2 рода принять не правильную.
16. Доверительный интервал – предельные значения статистической величины, которая с заданной доверительной вероятностью γ будет находится в этом интервале при выборке большего объема. Обозначается как P(θ - ε < x < θ + ε) = γ
Доверительная вероятность - вероятность найти измеряемую величину в данном доверительном интервале Т.е. чем уже интервал, в котором предположительно находтся измеряемая величина, тем меньше вероятность найти её в нем.


